अध्याय 04 रासायनिक बंधन और आणविक संरचना

Subject Hub

सामान्य Learning Resources

65%
Complete
12
Guides
8
Tests
5
Resources
7
Day Streak
Your Learning Path Active
✓
2
3
🎯
Learn Practice Test Master
📚
Study
📝
Test
📖
Plan
📊
Progress

वैज्ञानिक निरंतर नए यौगिकों की खोज करते हैं, उनके बारे में तथ्यों को क्रमबद्ध रूप से व्यवस्थित करते हैं, मौजूदा ज्ञान के साथ उन्हें समझाने का प्रयास करते हैं, पूर्व दृष्टिकोणों को संशोधित करने या नवनिरीक्षित तथ्यों को समझाने के लिए सिद्धांतों को विकसित करने के लिए संगठित होते हैं।

पदार्थ एक या विभिन्न प्रकार के तत्वों से बना होता है। सामान्य परिस्थितियों में, निर्जन गैसों को छोड़कर प्रकृति में कोई अन्य तत्व स्वतंत्र परमाणु के रूप में नहीं पाया जाता है। हालांकि, परमाणुओं का एक समूह एक प्रजाति के रूप में एक साथ पाया जाता है, जिसमें विशिष्ट गुण होते हैं। परमाणुओं के ऐसे समूह को अणु कहा जाता है। स्पष्ट है कि इन घटक परमाणुओं को अणु में एक साथ रखने वाला कोई बल होना चाहिए। आकर्षण बल जो विभिन्न रासायनिक प्रजातियों में विभिन्न घटकों (परमाणु, आयन आदि) को एक साथ रखता है, रासायनिक बंधन कहलाता है। चूंकि रासायनिक यौगिकों का निर्माण विभिन्न तत्वों के परमाणुओं के विभिन्न तरीकों से संयोजन के परिणामस्वरूप होता है, इससे कई प्रश्न उत्पन्न होते हैं। परमाणु संयोजन क्यों करते हैं? केवल कुछ संयोजन ही क्यों संभव हैं? कुछ परमाणु संयोजन क्यों करते हैं जबकि कुछ अन्य नहीं करते? अणुओं के निश्चित आकार क्यों होते हैं? ऐसे प्रश्नों के उत्तर देने के लिए समय-समय पर विभिन्न सिद्धांतों और अवधारणाओं को प्रस्तुत किया गया है। ये हैं कोसेल-लुईस दृष्टिकोण, संयोजी कोश इलेक्ट्रॉन युग्म प्रतिकर्षण (VSEPR) सिद्धांत, संयोजी बंध (VB) सिद्धांत और आण्विक कक्षक (MO) सिद्धांत। संयोजनता के विभिन्न सिद्धांतों का विकास और रासायनिक बंधनों की प्रकृति की व्याख्या परमाणु की संरचना की समझ, तत्वों की इलेक्ट्रॉनिक विन्यास और आवर्त सारणी में विकास से निकटता से संबंधित रहे हैं। प्रत्येक प्रणाली अधिक स्थिर होने की प्रवृत्ति रखती है और बंधन प्रणाली की ऊर्जा को कम कर स्थिरता प्राप्त करने की प्रकृति की विधि है।

4.1 रासायनिक बंधन के लिए कोसेल-लुईस दृष्टिकोण

रासायनिक बंधन के निर्माण को इलेक्ट्रॉनों के संदर्भ में समझाने के लिए कई प्रयास किए गए, लेकिन सन् 1916 में ही कोसेल और लुईस ने स्वतंत्र रूप से एक संतोषजनक व्याख्या देने में सफलता प्राप्त की। वे संयोजिता के किसी तार्किक स्पष्टीकरण को देने वाले पहले व्यक्ति थे, जो निष्क्रिय गैसों की निष्क्रियता पर आधारित था।

लुईस ने परमाणु को एक धनात्मक आवेशित ‘कर्नेल’ (नाभिक और आंतरिक इलेक्ट्रॉनों सहित) और बाह्य कोश के रूप में चित्रित किया, जो अधिकतम आठ इलेक्ट्रॉनों को समायोजित कर सकता है। उसने आगे यह माना कि ये आठ इलेक्ट्रॉन घन के कोनों पर स्थित होते हैं जो ‘कर्नेल’ को घेरे रहते हैं। इस प्रकार सोडियम का एकमात्र बाह्य कोश इलेक्ट्रॉन घन के एक कोने पर स्थित होगा, जबकि निष्क्रिय गैस के मामले में सभी आठ कोने भरे होंगे। इलेक्ट्रॉनों का यह अष्टक एक विशेष रूप से स्थिर इलेक्ट्रॉनिक व्यवस्था को दर्शाता है। लुईस ने यह माना कि परमाणु रासायनिक बंधों द्वारा जुड़ने पर स्थिर अष्टक प्राप्त करते हैं। सोडियम और क्लोरीन के मामले में यह सोडियम से क्लोरीन को एक इलेक्ट्रॉन के हस्तांतरण से हो सकता है, जिससे $\mathrm{Na}^+$ और $\mathrm{Cl}^{-}$ आयन बनते हैं। अन्य अणुओं जैसे $ \mathrm{Cl}_2, \mathrm{H}_2, \mathrm{~F}_2 $ आदि के मामले में, बंध परमाणुओं के बीच इलेक्ट्रॉनों के एक युग्म के साझा करने से बनता है। इस प्रक्रिया में प्रत्येक परमाणु बाह्य कोश का एक स्थिर अष्टक प्राप्त करता है।

लुइस प्रतीक: किसी अणु के निर्माण में केवल बाह्य कोश के इलेक्ट्रॉन ही रासायनिक संयोजन में भाग लेते हैं और इन्हें संयोजकता इलेक्ट्रॉन कहा जाता है। आंतरिक कोश के इलेक्ट्रॉन अच्छी तरह सुरक्षित होते हैं और सामान्यतः संयोजन प्रक्रिया में शामिल नहीं होते। G.N. लुइस, एक अमेरिकी रसायनज्ञ ने किसी परमाणु में संयोजकता इलेक्ट्रॉनों को दर्शाने के लिए सरल संकेतन प्रस्तुत किए। इन संकेतनों को लुइस प्रतीक कहा जाता है। उदाहरण के लिए, द्वितीय आवर्त के तत्वों के लिए लुइस प्रतीक नीचे दिए गए हैं:

लुइस प्रतीकों का महत्व: प्रतीक के चारों ओर बिंदुओं की संख्या संयोजकता इलेक्ट्रॉनों की संख्या को दर्शाती है। संयोजकता इलेक्ट्रॉनों की यह संख्या तत्व की सामान्य या वर्ग संयोजकता की गणना करने में सहायक होती है। तत्वों की वर्ग संयोजकता सामान्यतः या तो लुइस प्रतीकों में बिंदुओं की संख्या के बराबर होती है या 8 में से बिंदुओं या संयोजकता इलेक्ट्रॉनों की संख्या घटाने पर प्राप्त मान के बराबर होती है।

कॉसेल ने रासायनिक संयोजन के संदर्भ में निम्नलिखित तथ्यों की ओर ध्यान आकर्षित किया:

  • आवर्त सारणी में अत्यधिक विद्युत्-ऋणात्मक हैलोजन और अत्यधिक विद्युत्-धनात्मक क्षार धातुओं के बीच निष्क्रिय गैसें विभाजित करती हैं;
  • एक हैलोजन परमाणु से ऋणायन और एक क्षार धातु परमाणु से धनायन बनने की प्रक्रिया संबंधित परमाणुओं द्वारा इलेक्ट्रॉन के ग्रहण और त्याग से जुड़ी होती है;
  • इस प्रकार बने ऋणायन और धनायन स्थिर निष्क्रिय गैस इलेक्ट्रॉनिक विन्यास प्राप्त कर लेते हैं। निष्क्रिय गैसें (हेलियम को छोड़कर जिसके पास इलेक्ट्रॉनों की द्वयक होती है) के पास विशेष रूप से स्थिर बाह्य कोश विन्यास होता है जिसमें आठ (अष्टक) इलेक्ट्रॉन होते हैं, $n s^{2} n p^{6}$।
  • ऋणायन और धनायन स्थिर होते हैं विद्युत्-आकर्षण बल द्वारा।

उदाहरण के लिए, उपरोक्त योजना के अनुसार सोडियम और क्लोरीन से $\mathrm{NaCl}$ के निर्माण को इस प्रकार समझाया जा सकता है:
$\mathrm{Na}$ $\rightarrow$ $\mathrm{Na}^{+}+\mathrm{e}^{-}$
$[\mathrm{Ne}] 3 \mathrm{~s}^{1}$ $[\mathrm{Ne}]$
$\mathrm{Cl}+\mathrm{e}^{-}$ $\rightarrow$ $\mathrm{Cl}^{-}$
$[\mathrm{Ne}] 3 s^{2} 3 p^{5}$ $[\mathrm{Ne}] 3 s^{2} 3 p^{6}$ or $[\mathrm{Ar}]$
$\mathrm{Na}^{+}+\mathrm{Cl}^{-}$ $\rightarrow$ $\mathrm{NaCl}$ or $\mathrm{Na}^{+} \mathrm{Cl}^{-}$

इसी प्रकार $\mathrm{CaF}_{2}$ के निर्माण को दर्शाया जा सकता है:
$\mathrm{Ca}$ $\rightarrow$ $\mathrm{Ca}^{2+}+2 \mathrm{e}^{-}$
$[\mathrm{Ar}] 4 s^{2}$ $[\mathrm{Ar}]$
$\mathrm{F}+\mathrm{e}^{-}$ $\rightarrow$ $\mathrm{F}^{-}$
$[\mathrm{He}] 2 s^{2} 2 p^{5}$ $[\mathrm{He}] 2 s^{2} 2 p^{6}$ or $[\mathrm{Ne}]$
$\mathrm{Ca}^{2+}+2 \mathrm{~F}^{-}$ $\rightarrow$ $\mathrm{CaF}_2$ or $\mathrm{Ca}^{2+}\left(\mathrm{F}^{-}\right)_2$

धनात्मक और ऋणात्मक आयनों के बीच स्थिर वैद्युत आकर्षण के परिणामस्वरूप बना बंध, विद्युत-संयोजी बंध कहलाया। इस प्रकार विद्युत-संयोजकता आयन पर मौजूद इकाई आवेशों की संख्या के बराबर होती है। इसलिए, कैल्शियम को धनात्मक विद्युत-संयोजकता दो आवंटित की जाती है, जबकि क्लोरीन को ऋणात्मक विद्युत-संयोजकता एक।

कॉसेल की परिकल्पनाएँ आधुनिक संकल्पों का आधार प्रदान करती हैं जो इलेक्ट्रॉन स्थानांतरण द्वारा आयन-निर्माण और आयनिक क्रिस्टलीय यौगिकों के निर्माण से संबंधित हैं। उनके विचार आयनिक यौगिकों की समझ और वर्गीकरण में अत्यधिक मूल्य सिद्ध हुए हैं। साथ ही उन्होंने यह मान्यता भी दी कि बड़ी संख्या में यौगिक इन संकल्पों में फिट नहीं बैठते।

4.1.1 अष्टक नियम

कोसेल और लेविस ने 1916 में परमाणुओं के बीच रासायनिक संयोजन के एक महत्वपूर्ण सिद्धांत को विकसित किया जिसे रासायनिक बंधन का इलेक्ट्रॉनिक सिद्धांत कहा जाता है। इसके अनुसार, परमाणु अपने संयोजी इलेक्ट्रॉनों को एक परमाणु से दूसरे परमाणु में स्थानांतरित करके (प्राप्त करना या खोना) या संयोजी इलेक्ट्रॉनों को साझा करके संयोजन कर सकते हैं ताकि उनके संयोजी कोशों में अष्टक हो। इसे अष्टक नियम कहा जाता है।

4.1.2 सहसंयोजी बंध

लैंग्मुअर (1919) ने लेविस के प्रतिपादनों को परिष्कृत करते हुए अष्टक की स्थिर घनाकार व्यवस्था के विचार को त्याग दिया और सहसंयोजी बंध शब्द को प्रस्तुत किया। लेविस-लैंग्मुअर सिद्धांत को क्लोरीन अणु, $\mathrm{Cl}_2$, के निर्माण पर विचार करके समझा जा सकता है। $\mathrm{Cl}$ परमाणु, जिसकी इलेक्ट्रॉनिक विन्यास $[\mathrm{Ne}] 3 s^2 3 p^5$ है, आर्गॉन विन्यास से एक इलेक्ट्रॉन कम है। $\mathrm{Cl}_2$ अणु का निर्माण दो क्लोरीन परमाणुओं के बीच इलेक्ट्रॉनों के एक युग्म के साझा करने की संदर्भ में समझा जा सकता है, प्रत्येक क्लोरीन परमाणु साझा युग्म में एक इलेक्ट्रॉन योगदान करता है। इस प्रक्रिया में दोनों क्लोरीन परमाणु निकटतम निष्क्रिय गैस (अर्थात् आर्गॉन) की बाहरी कोश अष्टक प्राप्त कर लेते हैं।

दो Cl परमाणुओं के बीच सहसंयोजी बंध

बिंदु इलेक्ट्रॉनों को दर्शाते हैं। ऐसी संरचनाओं को लेविस बिंदु संरचनाएँ कहा जाता है।

लुइस डॉट संरचनाएं अन्य अणुओं के लिए भी लिखी जा सकती हैं, जिनमें संयोजी परमाणु समान या भिन्न हो सकते हैं। महत्वपूर्ण शर्तें यह हैं कि:

  • प्रत्येक बंधु परमाणुओं के बीच एक इलेक्ट्रॉन युग्म के साझाकरण के परिणामस्वरूप बनता है।
  • प्रत्येक संयोजी परमाणु साझे युग्म में कम-से-कम एक इलेक्ट्रॉन योगदान करता है।
  • संयोजी परमाणु इलेक्ट्रॉनों की साझेदारी के परिणामस्वरूप बाहरी कोश का नोबल गैस विन्यास प्राप्त करते हैं।
  • इस प्रकार जल और कार्बन टेट्राक्लोराइड अणुओं में सहसंयोजी बंधुओं का निर्माण इस प्रकार दर्शाया जा सकता है:

इस प्रकार, जब दो परमाणु एक इलेक्ट्रॉन युग्म साझा करते हैं, तो उन्हें एकल सहसंयोजी बंध द्वारा जोड़ा गया माना जाता है। कई यौगिकों में परमाणुओं के बीच एकाधिक बंध होते हैं। एकाधिक बंधों का निर्माण दो परमाणुओं के बीच एक से अधिक इलेक्ट्रॉन युग्म की साझेदारी की कल्पना करता है। यदि दो परमाणु दो इलेक्ट्रॉन युग्म साझा करते हैं, तो उनके बीच का सहसंयोजी बंध द्विबंध कहलाता है। उदाहरण के लिए, कार्बन डाइऑक्साइड अणु में कार्बन और ऑक्सीजन परमाणुओं के बीच दो द्विबंध होते हैं। इसी प्रकार एथीन अणु में दो कार्बन परमाणु एक द्विबंध द्वारा जुड़े होते हैं।

$\mathrm{C} _{2} \mathrm{H} _{4}$ अणु

जब परमाणु तीन इलेक्ट्रॉन युगलों को साझा करते हैं, जैसा कि $N_{2}$ अणु में दो नाइट्रोजन परमाणुओं और एथाइन अणु में दो कार्बन परमाणुओं के मामले में होता है, तो एक तिहरा बंध बनता है।

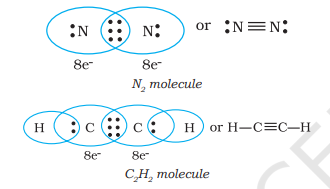
4.1.3 सरल अणुओं का लुइस प्रतिनिधित्व (लुइस संरचनाएँ)

लुइस डॉट संरचनाएँ अणुओं और आयनों में बंधन की एक तस्वीर प्रदान करती हैं, जो साझा किए गए इलेक्ट्रॉन युगलों और अष्टक नियम के संदर्भ में होती हैं। यद्यपि ऐसी तस्वीर किसी अणु के बंधन और व्यवहार को पूरी तरह से समझा नहीं सकती, फिर भी यह अणु के निर्माण और गुणों को काफी हद तक समझने में मदद करती है। इसलिए, अणुओं की लुइस डॉट संरचनाएँ लिखना बहुत उपयोगी होता है। लुइस डॉट संरचनाएँ निम्नलिखित चरणों को अपनाकर लिखी जा सकती हैं:

  • संरचनाओं को लिखने के लिए आवश्यक कुल इलेक्ट्रॉनों की संख्या संयोजित परमाणुओं के संयोजी इलेक्ट्रॉनों को जोड़कर प्राप्त की जाती है। उदाहरण के लिए, $\mathrm{CH}_{4}$ अणु में संयोजन के लिए आठ संयोजी इलेक्ट्रॉन उपलब्ध होते हैं (कार्बन से 4 और चार हाइड्रोजन परमाणुओं से 4)।
  • ऋणायनों के लिए, प्रत्येक ऋणात्मक आवेश का अर्थ होता है एक इलेक्ट्रॉन की वृद्धि। धनायनों के लिए, प्रत्येक धनात्मक आवेश के परिणामस्वरूप कुल संयोजी इलेक्ट्रॉनों की संख्या में से एक इलेक्ट्रॉन घट जाता है। उदाहरण के लिए, $CO_3^{2-}$ आयन के लिए, दो ऋणात्मक आवेश दर्शाते हैं कि तटस्थ परमाणुओं द्वारा प्रदान किए गए इलेक्ट्रॉनों की तुलना में दो अतिरिक्त इलेक्ट्रॉन हैं। $\mathrm{NH}_{4}^{+}$ आयन के लिए, एक धनात्मक आवेश तटस्थ परमाणुओं के समूह से एक इलेक्ट्रॉन की हानि को दर्शाता है।
  • संयोजित परमाणुओं के रासायनिक प्रतीकों को जानना और यौगिक की कंकालीय संरचना का ज्ञान होना (ज्ञात या बुद्धिमानी से अनुमानित), कुल इलेक्ट्रॉनों की संख्या को संयोजी साझा युग्मों के रूप में परमाणुओं के बीच कुल बंधों के अनुपात में वितरित करना आसान बनाता है।
  • सामान्यतः सबसे कम विद्युतऋणात्मक परमाणु अणु/आयन में केंद्रीय स्थान पर होता है। उदाहरण के लिए $\mathrm{NF}_3$ और $CO_3^{2-}$ में, नाइट्रोजन और कार्बन केंद्रीय परमाणु हैं जबकि फ्लोरीन और ऑक्सीजन सिरों पर स्थित होते हैं।
  • एकल बंधों के लिए साझा इलेक्ट्रॉन युग्मों की गणना करने के बाद, शेष इलेक्ट्रॉन युग्म या तो बहु-बंधन के लिए उपयोग किए जाते हैं या एकाकी युग्मों के रूप में रहते हैं। मूल आवश्यकता यह है कि प्रत्येक संयोजित परमाणु को इलेक्ट्रॉनों का एक अष्टक प्राप्त हो।

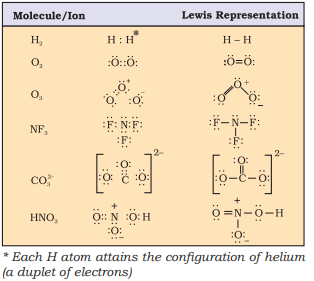
कुछ अणुओं/आयनों के लुईस चित्रण को सारणी 4.1 में दिया गया है।

सारणी 4.1 कुछ अणुओं का लुईस चित्रण

समस्या 4.1

$\mathrm{CO}$ अणु का लुईस बिन्दु संरचना लिखिए।

हल

चरण 1. कार्बन और ऑक्सीजन परमाणुओं की संयुक्त बाह्य (संयोजकता) इलेक्ट्रॉनों की कुल संख्या गिनिए। कार्बन और ऑक्सीजन परमाणुओं की बाह्य (संयोजकता) कोश संरचनाएँ क्रमशः: $2 s^{2} 2 p^{2}$ और $2 s^{2} 2 p^{4}$ हैं। उपलब्ध संयोजकता इलेक्ट्रॉन $4+6=10$ हैं।

चरण 2. $\mathrm{CO}$ की आकृति संरचना इस प्रकार लिखी जाती है: C O

चरण 3. $\mathrm{C}$ और $\mathrm{O}$ के बीच एकल बंध (एक साझा इलेक्ट्रॉन युग्म) खींचिए और $\mathrm{O}$ पर अष्टक पूर्ण कीजिए, शेष दो इलेक्ट्रॉन $\mathrm{C}$ पर एकाकी युग्म बनाते हैं।

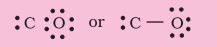
इससे कार्बन पर अष्टक पूर्ण नहीं होता और इसलिए हमें $\mathrm{C}$ और $\mathrm{O}$ परमाणुओं के बीच बहु-बंधन (इस स्थिति में त्रिपल बंध) करना पड़ता है। यह दोनों परमाणुओं के लिए अष्टक नियम की स्थिति को संतुष्ट करता है।

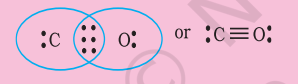
प्रश्न 4.2

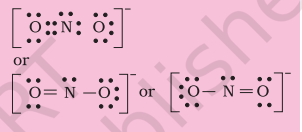
नाइट्राइट आयन, $\mathrm{NO}_{2}^{-}$ की लुइस संरचना लिखिए।

हल

चरण 1. नाइट्रोजन परमाणु, ऑक्सीजन परमाणुओं और एक अतिरिक्त ऋणात्मक आवेश (एक इलेक्ट्रॉन के बराबर) के संयुक्त वैलेंस इलेक्ट्रॉनों की कुल संख्या गिनिए।

$$ \begin{aligned} & \mathrm{N}\left(2 s^{2} 2 p^{3}\right), \mathrm{O}\left(2 s^{2} 2 p^{4}\right) \\ & 5+(2 \times 6)+ = 17 \text { इलेक्ट्रॉन } \end{aligned} $$

एक इकाई ऋणात्मक आवेश के लिए एक इलेक्ट्रॉन जोड़ने पर इलेक्ट्रॉनों की कुल संख्या = 17+1 = 18

चरण 2. $\mathrm{NO}_{2}^{-}$ की कंकाल संरचना इस प्रकार लिखी जाती है: $\mathrm{O} \quad \mathrm{N} \mathrm{O}$

चरण 3. नाइट्रोजन और प्रत्येक ऑक्सीजन परमाणु के बीच एकल बंधन (एक साझा इलेक्ट्रॉन युग्म) बनाइए जिससे ऑक्सीजन परमाणुओं की अष्टक पूरी हो जाए। यदि शेष दो इलेक्ट्रॉन नाइट्रोजन पर एकाकी युग्म बनाते हैं, तो इससे नाइट्रोजन की अष्टक पूरी नहीं होती।

इसलिए हमें नाइट्रोजन और एक ऑक्सीजन परमाणु के बीच गुण बंधन (इस स्थिति में द्विबंध) बनाना पड़ता है। इससे निम्नलिखित लुइस बिंदु संरचनाएँ प्राप्त होती हैं।

4.1.4 औपचारिक आवेश

लुईस बिंदु संरचनाएं, सामान्यतः, अणुओं की वास्तविक आकृतियों का प्रतिनिधित्व नहीं करती हैं। बहुपरमाण्विक आयनों के मामले में, शुद्ध आवेश संपूर्ण आयन द्वारा धारित होता है न कि किसी विशेष परमाण्व द्वारा। यह, हालांकि, प्रत्येक परमाणु पर एक औपचारिक आवेश निर्धारित करना संभव है। बहुपरमाण्विक अणु या आयन में किसी परमाणु का औपचारिक आवेश उस परमाणु के संयोजी इलेक्ट्रॉनों की संख्या और लुईस संरचना में उस परमाणु को सौंपे गए इलेक्ट्रॉनों की संख्या के बीच के अंतर के रूप में परिभाषित किया जा सकता है। इसे इस प्रकार व्यक्त किया जाता है:

गणना इस धारणा पर आधारित है कि अणु में परमाणु प्रत्येक साझा किए गए युगल का एक इलेक्ट्रॉन और एकाकी युगल के दोनों इलेक्ट्रॉन स्वामित्व करता है।

आइए ओजोन अणु $\left(\mathrm{O}_3\right)$ पर विचार करें। $\mathrm{O}_3$ की लुईस संरचना इस प्रकार खींची जा सकती है:

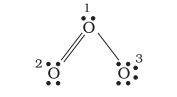
परमाणुओं को 1, 2 और 3 के रूप में अंकित किया गया है। पर औपचारिक आवेश:

  • केंद्रीय $\mathrm{O}$ परमाणु जिसे 1 चिह्नित किया गया है $=6-2-\frac{1}{2}(6)=+1$
  • अंत $\mathrm{O}$ परमाणु जिसे 2 चिह्नित किया गया है $=6-4-\frac{1}{2}(4)=0$
  • अंत $\mathrm{O}$ परमाणु जिसे 3 चिह्नित किया गया है $=6-6-\frac{1}{2}(2)=-1$

इसलिए, हम $\mathrm{O}_{3}$ को औपचारिक आवेशों के साथ इस प्रकार दर्शाते हैं:

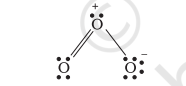
हमें यह समझना चाहिए कि औपचारिक आवेश अणु के भीतर वास्तविक आवेश पृथक्करण को इंगित नहीं करते हैं। लुईस संरचना में परमाणुओं पर आवेश दर्शाना केवल अणु में संयोजी इलेक्ट्रॉनों को ट्रैक करने में मदद करता है। औपचारिक आवेश किसी दिए गए प्रजाति के लिए संभावित लुईस संरचनाओं में से न्यूनतम ऊर्जा संरचना के चयन में मदद करते हैं। आमतौर पर न्यूनतम ऊर्जा संरचना वह होती है जिसमें परमाणुओं पर सबसे छोटे औपचारिक आवेश हों। औपचारिक आवेश एक ऐसा कारक है जो आबंधन के शुद्ध सहसंयोजक दृष्टिकोण पर आधारित है जिसमें इलेक्ट्रॉन युग्म पड़ोसी परमाणुओं द्वारा समान रूप से साझा किए जाते हैं।

4.1.5 अष्टक नियम की सीमाएँ

अष्टक नियम, यद्यपि उपयोगी है, सार्वभौमिक नहीं है। यह अधिकांश कार्बनिक यौगिकों की संरचनाओं को समझने के लिए काफी उपयोगी है और यह मुख्य रूप से आवर्त सारणी के द्वितीय आवर्त के तत्वों पर लागू होता है। अष्टक नियम के तीन प्रकार के अपवाद होते हैं।

केंद्रीय परमाणु का अपूर्ण अष्टक

कुछ यौगिकों में, केंद्रीय परमाणु के चारों ओर इलेक्ट्रॉनों की संख्या आठ से कम होती है। यह विशेष रूप से उन तत्वों के साथ होता है जिनमें चार से कम संयोजक इलेक्ट्रॉन होते हैं। उदाहरण हैं $\mathrm{LiCl}$, $\mathrm{BeH}_2$ और $\mathrm{BCl}_3$।

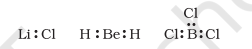
$\mathrm{Li}$, Be और B के पास क्रमशः 1, 2 और 3 संयोजक इलेक्ट्रॉन होते हैं। कुछ अन्य ऐसे यौगिक हैं $\mathrm{AlCl}_3$ और $\mathrm{BF}_3$।

विषम-इलेक्ट्रॉन अणु

ऐसे अणुओं में जिनमें इलेक्ट्रॉनों की संख्या विषम होती है, जैसे नाइट्रिक ऑक्साइड, $\mathrm{NO}$ और नाइट्रोजन डाइऑक्साइड, $\mathrm{NO}_2$, सभी परमाणुओं के लिए अष्टक नियम संतुष्ट नहीं होता है।

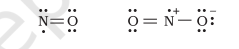
विस्तारित अष्टक

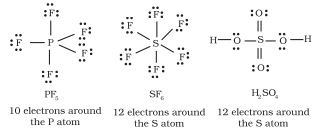
आवर्त सारणी की तीसरी अवधि और उससे आगे के तत्वों के पास $3s$ और $3p$ कक्षकों के अतिरिक्त $3d$ कक्षक भी उपलब्ध होते हैं संयोजन के लिए। इन तत्वों के कई यौगिकों में केंद्रीय परमाणु के चारों ओर आठ से अधिक संयोजक इलेक्ट्रॉन होते हैं। इसे विस्तारित अष्टक कहा जाता है। स्पष्ट रूप से ऐसे मामलों में अष्टक नियम लागू नहीं होता है।

ऐसे यौगिकों के कुछ उदाहरण हैं: $\mathrm{PF}_5$, $\mathrm{SF}_6$, $\mathrm{H}_2 \mathrm{SO}_4$ और कई समन्वय यौगिक।

दिलचस्प बात यह है कि सल्फर ऐसे कई यौगिक भी बनाता है जिनमें अष्टक नियम का पालन होता है। सल्फर डाइक्लोराइड में, $\mathrm{S}$ परमाणु के चारों ओर इलेक्ट्रॉनों का अष्टक होता है।

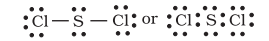
अष्टक सिद्धांत की अन्य कमियाँ

  • यह स्पष्ट है कि अष्टक नियम उन गैसों की रासायनिक निष्क्रियता पर आधारित है जो निर्वात गैसें हैं। हालांकि, कुछ निर्वात गैसें (उदाहरण के लिए जेनॉन और क्रिप्टॉन) ऑक्सीजन और फ्लोरीन के साथ मिलकर $\mathrm{XeF}_2$, $\mathrm{KrF}_2$, $\mathrm{XeOF}_2$ आदि जैसे कई यौगिक भी बनाती हैं।
  • यह सिद्धांत अणुओं के आकार की व्याख्या नहीं करता।
  • यह अणुओं की सापेक्ष स्थिरता की व्याख्या नहीं करता और अणु की ऊर्जा के बारे में पूरी तरह से चुप रहता है।

4.2 आयनिक या विद्युत-संयोजी बंध

कोसेल और लुइस द्वारा आयनिक बंध के निर्माण के उपचार से यह स्पष्ट होता है कि आयनिक यौगिकों का निर्माण मुख्यतः इस बात पर निर्भर करेगा:

  • संबंधित उदासीन परमाणुओं से धनात्मक और ऋणात्मक आयनों के बनने में आसानी;
  • ठोस में धनात्मक और ऋणात्मक आयनों की व्यवस्था, अर्थात् क्रिस्टलीय यौगिक का जालक।

धनात्मक आयन के निर्माण में आयनन सम्मिलित होता है, अर्थात् उदासीन परमाणु से इलेक्ट्रॉन(ों) को हटाना, और ऋणात्मक आयन के निर्माण में उदासीन परमाणु में इलेक्ट्रॉन(ों) को जोड़ना शामिल है।
$\mathrm{M}(\mathrm{g}) $ $\rightarrow$ $\mathrm{M}^{+}(\mathrm{g})+\mathrm{e}^{-} ;$
आयनन एन्थैल्पी
$\mathrm{X}(\mathrm{g})+\mathrm{e}^{-}$ $\rightarrow$ $\mathrm{X}^{-}(\mathrm{g}) ;$
इलेक्ट्रॉन लब्धि एन्थैल्पी
$\mathrm{M}^{+}(\mathrm{g})+\mathrm{X}^{-}(\mathrm{g}) \rightarrow$ $\mathrm{MX}(\mathrm{s})$

इलेक्ट्रॉन लब्धि एन्थैल्पी, $\Delta_{e g} \boldsymbol{H}$, वह एन्थैल्पी परिवर्तन है (इकाई 3), जब गैसीय अवस्था में स्थित आधारभूत अवस्था का परमाणु एक इलेक्ट्रॉन ग्रहण करता है। इलेक्ट्रॉन लब्धि प्रक्रिया बाह्यउष्मक या अंतःउष्मक हो सकती है। दूसरी ओर, आयनन सदैव अंतःउष्मक होता है। इलेक्ट्रॉन सहचारिता, इलेक्ट्रॉन लब्धि के साथ होने वाली ऊर्जा परिवर्तन का ऋणात्मक है।

स्पष्टतः आयनिक आबंध उन तत्वों के बीच अधिक आसानी से बनेंगे जिनकी आयनन एन्थैल्पी तुलनात्मक रूप से कम हो और जिनकी इलेक्ट्रॉन लब्धि एन्थैल्पी तुलनात्मक रूप से उच्च ऋणात्मक मान रखती हो।

अधिकांश आयनिक यौगिकों में धात्विक तत्वों से प्राप्त धनायन और अधात्विक तत्वों से प्राप्त ऋणायन होते हैं। अमोनियम आयन, $\mathrm{NH}_{4}^{+}$(जो दो अधात्विक तत्वों से बना है) एक अपवाद है। यह कई आयनिक यौगिकों का धनायन बनाता है।

क्रिस्टलीय अवस्था में आयनिक यौगिक धनायनों और ऋणायनों के एक क्रमबद्ध त्रि-आयामी व्यवस्था से बने होते हैं जो कूलॉम्बी अन्योन्यक्रिया ऊर्जा द्वारा एक साथ बंधे रहते हैं। ये यौगिक विभिन्न क्रिस्टल संरचनाओं में क्रिस्टलीकृत होते हैं जो आयनों के आकार, उनकी पैकिंग व्यवस्था और अन्य कारकों द्वारा निर्धारित होती हैं। सोडियम क्लोराइड, $\mathrm{NaCl}$ (रॉक सॉल्ट) की क्रिस्टल संरचना, उदाहरण के लिए नीचे दिखाई गई है।

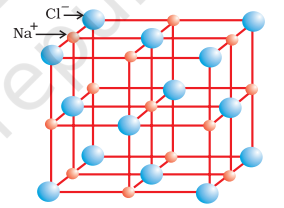
रॉक सॉल्ट संरचना

आयनिक ठोसों में, इलेक्ट्रॉन लाभ एन्थैल्पी और आयनन एन्थैल्पी का योग धनात्मक हो सकता है, फिर भी क्रिस्टल जालक बनने के दौरान निकलने वाली ऊर्जा के कारण क्रिस्टल संरचना स्थिर हो जाती है। उदाहरण के लिए: $\mathrm{Na}(\mathrm{g})$ से $\mathrm{Na}^{+}(\mathrm{g})$ बनने की आयनन एन्थैल्पी $495.8 \mathrm{~kJ} \mathrm{~mol}^{-1}$ है; जबकि $\mathrm{Cl}(\mathrm{g})+\mathrm{e}^{-} \rightarrow$ $\mathrm{Cl}^{-}(\mathrm{g})$ परिवर्तन के लिए इलेक्ट्रॉन लाभ एन्थैल्पी केवल $-348.7 \mathrm{~kJ} \mathrm{~mol}^{-1}$ है। इन दोनों का योग, $147.1 \mathrm{~kJ} \mathrm{~mol}^{-1}$, $\mathrm{NaCl}(\mathrm{s})$ की जालक-निर्माण एन्थैल्पी $\left(-788 \mathrm{~kJ} \mathrm{~mol}^{-1}\right)$ से कहीं अधिक संतुलित हो जाता है। इसलिए, इन प्रक्रियाओं में निकलने वाली ऊर्जा अवशोषित ऊर्जा से अधिक होती है। इस प्रकार किसी आयनिक यौगिक की स्थिरता का गुणात्मक माप इसकी जालक-निर्माण एन्थैल्पी द्वारा दिया जाता है, न कि केवल गैसीय अवस्था में आयनिक प्रजाति के चारों ओर अष्टक प्राप्त करने से।

चूँकि जालक एन्थैल्पी आयनिक यौगिकों के निर्माण में प्रमुख भूमिका निभाती है, यह आवश्यक है कि हम इसके बारे में और अधिक जानें।

4.2.1 जालक एन्थैल्पी

एक आयनिक ठोस की जालक एन्थैल्पी को परिभाषित किया जाता है ऊर्जा के रूप में जो एक मोल ठोस आयनिक यौगिक को उसके गैसीय घटक आयनों में पूरी तरह अलग करने के लिए आवश्यक हो। उदाहरण के लिए, $\mathrm{NaCl}$ की जालक एन्थैल्पी $788 \mathrm{~kJ} \mathrm{~mol}^{-1}$ है। इसका अर्थ है कि 788 $\mathrm{kJ}$ ऊर्जा की आवश्यकता होती है एक मोल ठोस $\mathrm{NaCl}$ को एक मोल $\mathrm{Na}^{+}(\mathrm{g})$ और एक मोल $\mathrm{Cl}^{-}(\mathrm{g})$ में अनंत दूरी तक अलग करने के लिए।

इस प्रक्रिया में विपरीत आवेशों वाले आयनों के बीच आकर्षण बल और समान आवेशों वाले आयनों के बीच प्रतिकर्षण बल दोनों शामिल होते हैं। ठोस क्रिस्टल त्रि-आयामी होता है; इसलिए केवल आकर्षण और प्रतिकर्षण बलों की अन्योन्य क्रिया से जालक एन्थैल्पी की सीधी गणना संभव नहीं है। क्रिस्टल ज्यामिति से जुड़े कारकों को भी शामिल करना पड़ता है।

4.3 बंध पैरामीटर

4.3.1 बंध लंबाई

बंध लंबाई को परिभाषित किया जाता है दो बंधित परमाणुओं के नाभिकों के बीच की साम्यावस्था दूरी के रूप में एक अणु में। बंध लंबाइयों को स्पेक्ट्रोस्कोपिक, एक्स-रे विवर्तन और इलेक्ट्रॉन-विवर्तन तकनीकों द्वारा मापा जाता है जिनके बारे में आप उच्च कक्षाओं में सीखेंगे। बंधित युग्म का प्रत्येक परमाणु बंध लंबाई में योगदान देता है (चित्र 4.1)। सहसंयोजक बंध के मामले में, प्रत्येक परमाणु से योगदान को उस परमाणु की सहसंयोजक त्रिज्या कहा जाता है।

सहसंयोजक त्रिज्या लगभग उस परमाणु के नाभिक की त्रिज्या के रूप में मापी जाती है जो संयोजित स्थिति में संलग्न परमाणु के नाभिक के संपर्क में हो। सहसंयोजक त्रिज्या उसी अणु में सहसंयोजक बंध द्वारा जुड़े दो समान परमाणुओं के बीच की दूरी की आधी होती है।

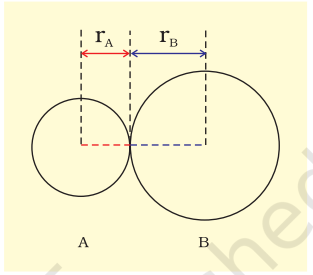
चित्र 4.1 सहसंयोजक अणु AB में बंध लंबाई। R = rA + rB (R बंध लंबाई है और rA तथा rB क्रमशः परमाणु A और B की सहसंयोजक त्रिज्याएँ हैं)

वान डेर वाल्स त्रिज्या परमाणु के समग्र आकार को दर्शाती है जिसमें इसकी संयोजी कोश गैर-संयोजित स्थिति में सम्मिलित होती है। इसके अतिरिक्त, वान डेर वाल्स त्रिज्या ठोस में पृथक अणुओं में स्थित दो समान परमाणुओं के बीच की दूरी की आधी होती है। क्लोरीन की सहसंयोजक और वान डेर वाल्स त्रिज्याओं को चित्र 4.2 में दर्शाया गया है।

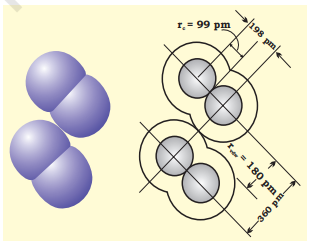
चित्र 4.2 क्लोरीन अणु में सहसंयोजक और वान डेर वाल्स त्रिज्याएँ। आंतरिक वृत्त क्लोरीन परमाणु के आकार के अनुरूप हैं (rvdw और rc क्रमशः वान डेर वाल्स और सहसंयोजक त्रिज्याएँ हैं)।

एकल, द्वि और त्रिपल आबंधों के कुछ सामान्य औसत आबंध लंबाइयाँ सारणी 4.2 में दिखाई गई हैं। कुछ सामान्य अणुओं के लिए आबंध लंबाइयाँ सारणी 4.3 में दी गई हैं।

कुछ सामान्य तत्वों की सहसंयोजक त्रिज्याएँ सारणी 4.4 में सूचीबद्ध हैं।

4.3.2 आबंध कोण

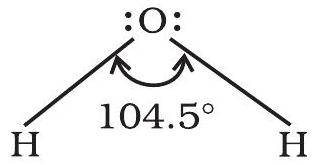
इसे अणु/संकुल आयन में केंद्रीय परमाणु के चारों ओर आबंध इलेक्ट्रॉन युगलों को धारण करने वाली कक्षाओं के बीच का कोण परिभाषित किया गया है। आबंध कोण डिग्री में व्यक्त किया जाता है जिसे स्पेक्ट्रोस्कोपी विधियों द्वारा प्रायोगिक रूप से निर्धारित किया जा सकता है। यह अणु/संकुल आयन में केंद्रीय परमाणु के चारों ओर कक्षाओं के वितरण के संबंध में कुछ विचार देता है और इसलिए यह हमें इसके आकार का निर्धारण करने में मदद करता है। उदाहरण के लिए जल में $\mathrm{H}-\mathrm{O}-\mathrm{H}$ आबंध कोण इस प्रकार दर्शाया जा सकता है :

4.3.3 आबंध एन्थैल्पी

इसे गैसीय अवस्था में दो परमाणुओं के बीच एक विशेष प्रकार के आबंध की एक मोल टूटने के लिए आवश्यक ऊर्जा की मात्रा के रूप में परिभाषित किया गया है। आबंध एन्थैल्पी की इकाई $\mathrm{kJ} \mathrm{mol}^{-1}$ है। उदाहरण के लिए, हाइड्रोजन अणु में $\mathrm{H}-\mathrm{H}$ आबंध एन्थैल्पी $435.8 \mathrm{~kJ} \mathrm{~mol}^{-1}$ है।

$\mathrm{H}_2 (\mathrm{~g}) \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{H}(\mathrm{g})$;

$\Delta_{\mathrm{a}} H^\ominus =435.8 \mathrm{~kJ} \mathrm{~mol}^{-1}$

इसी प्रकार बहुबंध युक्त अणुओं, उदाहरण के लिए $\mathrm{O}_2$ और $\mathrm{N}_2$ के लिए बंध एन्थैल्पी निम्नलिखित होगी :

$\mathrm{O}_{2}(\mathrm{O}=\mathrm{O})(\mathrm{g}) \rightarrow \mathrm{O}(\mathrm{g})+\mathrm{O}(\mathrm{g}) ;$

$$ \Delta_{\mathrm{a}} H^{\ominus}=498 \mathrm{~kJ} \mathrm{~mol}^{-1} $$

$\mathrm{N}_{2}(\mathrm{~N} \equiv \mathrm{N})(\mathrm{g}) \rightarrow \mathrm{N}(\mathrm{g})+\mathrm{N}(\mathrm{g}) ;$

$$ \Delta_{\mathrm{a}} H^{\ominus}=946.0 \mathrm{~kJ} \mathrm{~mol}^{-1} $$

यह महत्वपूर्ण है कि बंध विघटन एन्थैल्पि जितनी अधिक होगी, अणु में बंध उतना ही मजबूत होगा। एक विषमनाभिक द्विआणुक अणु जैसे $\mathrm{HCl}$ के लिए, हमारे पास

$$ \mathrm{HCl}(\mathrm{g}) \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{Cl}(\mathrm{g}) ; \Delta_{\mathrm{a}} \mathrm{H}^{\ominus}=431.0 \mathrm{~kJ} \mathrm{~mol}^{-1} $$

बहुआणुक अणुओं के मामले में, बंध सामर्थ्य की माप अधिक जटिल होती है। उदाहरण के लिए $\mathrm{H}_{2} \mathrm{O}$ अणु के मामले में, दो $\mathrm{O}-\mathrm{H}$ बंधों को तोड़ने के लिए आवश्यक एन्थैल्पी समान नहीं होती।

तालिका 4.2 कुछ एकल, द्वि और त्रिपल बंधों के लिए औसत बंध लंबाई

बंध प्रकार सहसंयोजी बंध लंबाई (pm)
$\mathrm{O}-\mathrm{H}$ 96
$\mathrm{C}-\mathrm{H}$ 107
$\mathrm{~N}-\mathrm{O}$ 136
$\mathrm{C}-\mathrm{O}$ 143
$\mathrm{C}-\mathrm{N}$ 143
$\mathrm{C}-\mathrm{C}$ 154
$\mathrm{C}=\mathrm{O}$ 121
$\mathrm{~N}=\mathrm{O}$ 122
$\mathrm{C}=\mathrm{C}$ 133
$\mathrm{C}=\mathrm{N}$ 138
$\mathrm{C} \equiv \mathrm{N}$ 116
$\mathrm{C} \equiv \mathrm{C}$ 120

तालिका 4.3 कुछ सामान्य अणुओं में बंध लंबाइयाँ

अणु बंध लंबाई (pm)
$\mathrm{H}_{2}(\mathrm{H}-\mathrm{H})$ 74
$\mathrm{~F}_{2}(\mathrm{~F}-\mathrm{F})$ 144
$\mathrm{Cl}_{2}(\mathrm{Cl}-\mathrm{Cl})$ 199
$\mathrm{Br}_{2}(\mathrm{Br}-\mathrm{Br})$ 228
$\mathrm{I}_{2}(\mathrm{I}-\mathrm{I})$ 267
$\mathrm{~N}_{2}(\mathrm{~N} \equiv \mathrm{N})$ 109
$\mathrm{O}_{2}(\mathrm{O}=\mathrm{O})$ 121
$\mathrm{HF}(\mathrm{H}-\mathrm{F})$ 92
$\mathrm{HCl}(\mathrm{H}-\mathrm{Cl})$ 127
$\mathrm{HBr}(\mathrm{H}-\mathrm{Br})$ 141
$\mathrm{HI}(\mathrm{H}-\mathrm{I})$ 160

तालिका 4.4 सहसंयोजी त्रिज्याएँ, $ \mathbf{r}_{\text {cov }} /(\mathrm{pm})$

$\mathrm{H}$ 37
$\mathrm{C}$ $77(1)$ $\mathrm{N}$ $74(1)$ $\mathrm{O}$ $66(1)$ $\mathrm{F}$ 64
$67(2)$ $65(2)$ $57(2)$ $\mathrm{Cl}$ 99
$60(3)$ $55(3)$
$\mathrm{P}$ 110 $\mathrm{~S}$ $104(1)$ $\mathrm{Br}$ 114
$95(2)$
$\mathrm{As}$ 121 $\mathrm{Se}$ 104 $\mathrm{I}$ 133
$\mathrm{Sb}$ 141 $\mathrm{Te}$ 137
  • उद्धृत मान एकल बंधों के लिए हैं, जब तक कि कोष्ठक में अन्यथा उल्लिखित न हो। (आवर्ती प्रवृत्तियों के लिए इकाई 3 भी देखें)।

$\mathrm{H}_2 \mathrm{O}(\mathrm{g}) \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{OH}(\mathrm{g}) ; \Delta_a H_1^\ominus=502 \mathrm{~kJ} \mathrm{~mol}^{-1}$

$\mathrm{OH}(\mathrm{g}) \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{O}(\mathrm{g}) ; \Delta_{\mathrm{a}} H_{2}^{\ominus}=427 \mathrm{~kJ} \mathrm{~mol}^{-1}$

$\Delta_{\mathrm{a}} H^{\ominus}$ के मान में अंतर दर्शाता है कि दूसरा $\mathrm{O}-\mathrm{H}$ बंध रासायनिक वातावरण में बदलाव के कारण कुछ बदलाव से गुजरता है। यही कारण है कि $\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}$ (एथेनॉल) और पानी जैसे विभिन्न अणुओं में समान $\mathrm{O}-\mathrm{H}$ बंध की ऊर्जा में कुछ अंतर होता है। इसलिए बहुपरमाणुक अणुओं में औसत या माध्य बंध एन्थैल्पी शब्द का प्रयोग किया जाता है। इसे कुल बंध वियोजन एन्थैल्पी को टूटे हुए बंधों की संख्या से विभाजित करके प्राप्त किया जाता है जैसा कि नीचे पानी के अणु के मामले में समझाया गया है,

$ \text { औसत बंध एन्थैल्पी } =\frac{502+427}{2} $

$$ =464.5 \mathrm{~kJ} \mathrm{~mol}^{-1} $$

4.3.4 बंध क्रम

सहसंयोजी बंध के लुइस वर्णन में, बंध क्रम को अणु में दो परमाणुओं के बीच बंधों की संख्या द्वारा दिया जाता है। बंध क्रम, उदाहरण के लिए $\mathrm{H}_2$ में (एक साझा इलेक्ट्रॉन युग्म के साथ), $\mathrm{O}_2$ में (दो साझा इलेक्ट्रॉन युग्मों के साथ) और $\mathrm{N}_2$ में (तीन साझा इलेक्ट्रॉन युग्मों के साथ) क्रमशः $1,2,3$ है। इसी प्रकार CO में ($\mathrm{C}$ और $\mathrm{O}$ के बीच तीन साझा इलेक्ट्रॉन युग्म) बंध क्रम 3 है। $\mathrm{N}_2$ के लिए, बंध क्रम 3 है और इसकी $\Delta_a H^\ominus$ $946 \mathrm{~kJ} \mathrm{~mol}^{-1}$ है; यह द्विपरमाणुक अणु के लिए सबसे अधिक में से एक है।

समइलेक्ट्रॉनिक अणु तथा आयनों की बंध कोटियाँ समान होती हैं; उदाहरण के लिए, $F_2$ तथा $\mathrm{O}_{2}^{2-}$ की बंध कोटि 1 है। $\mathrm{N}_2, \mathrm{CO}$ तथा $\mathrm{NO}^{+}$ की बंध कोटि 3 है।

अणुओं की स्थिरता को समझने के लिए एक सामान्य संबंध यह है कि: बंध कोटि बढ़ने के साथ बंध एन्थैल्पी बढ़ती है और बंध लंबाई घटती है।

4.3.5 अनुनाद संरचनाएँ

अक्सर यह देखा जाता है कि किसी अणु के प्रयोगात्मक रूप से निर्धारित प्राचलों के अनुरूप उसका प्रतिनिधित्व करने के लिए एकल लुइस संरचना अपर्याप्त होती है। उदाहरण के लिए, ओज़ोन, $\mathrm{O}_{3}$ अणु को नीचे दर्शाए गए संरचना I और II दोनों से समान रूप से दर्शाया जा सकता है:

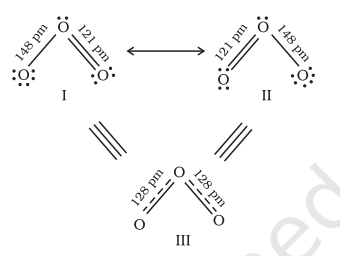
चित्र 4.3 O3 अणु में अनुनाद

(संरचना I और II दोनों मानक रूपों को दर्शाती हैं जबकि संरचना III अनुनाद हाइब्रिड है)

दोनों संरचनाओं में हमारे पास एक $\mathrm{O}-\mathrm{O}$ एकल बंधन और एक $\mathrm{O}=\mathrm{O}$ द्विबंध है। सामान्य $\mathrm{O}-\mathrm{O}$ और $\mathrm{O}=\mathrm{O}$ बंध लंबाई क्रमशः $148 \mathrm{pm}$ और $121 \mathrm{pm}$ हैं। प्रयोगात्मक रूप से निर्धारित ऑक्सीजन-ऑक्सीजन बंध लंबाई $\mathrm{O}_3$ अणु में समान हैं ($128 \mathrm{pm}$)। इस प्रकार $\mathrm{O}_3$ अणु में ऑक्सीजन-ऑक्सीजन बंध एक द्विबंध और एकल बंध के बीच की स्थिति के होते हैं। स्पष्ट है कि इसे ऊपर दिखाई गई दो लुइस संरचनाओं में से किसी एक द्वारा नहीं दर्शाया जा सकता।

अनुनाद (रेसोनेंस) की अवधारणा $\mathrm{O}_3$ जैसे अणुओं की सटीक संरचनाओं के चित्रण में आने वाली कठिनाइयों से निपटने के लिए प्रस्तुत की गई थी। अनुनाद की अवधारणा के अनुसार, जब भी कोई एकल लुइस संरचना किसी अणु को सटीक रूप से वर्णित नहीं कर सकती, तो समान ऊर्जा, नाभिकों की स्थिति, बंधन और गैर-बंधन इलेक्ट्रॉन युग्मों वाली कई संरचनाओं को हाइब्रिड की कैनोनिकल संरचनाओं के रूप में लिया जाता है जो अणु को सटीक रूप से वर्णित करती हैं। इस प्रकार $\mathrm{O}_3$ के लिए, ऊपर दिखाई गई दो संरचनाएं कैनोनिकल संरचनाएं या अनुनाद संरचनाएं हैं और उनका हाइब्रिड अर्थात् तीसरी संरचना $\mathrm{O}_3$ की संरचना को अधिक सटीक रूप से दर्शाती है। इसे अनुनाद हाइब्रिड भी कहा जाता है। अनुनाद को दोहरी तीर द्वारा दर्शाया जाता है।

अनुनाद संरचनाओं के कुछ अन्य उदाहरण कार्बोनेट आयन और कार्बन डाइऑक्साइड अणु द्वारा प्रदान किए जाते हैं।

प्रश्न 4.3

$\mathrm{CO}_{3}^{2-}$ आयन की संरचना को अनुनाद के संदर्भ में समझाइए।

हल

कार्बन और ऑक्सीजन परमाणुओं के बीच दो एकल बंधों और एक द्विबंध की उपस्थिति पर आधारित एकल लुइस संरचना अणु को सटीक रूप से दर्शाने के लिए अपर्याप्त है क्योंकि यह असमान बंधों को दर्शाती है। प्रयोगात्मक परिणामों के अनुसार, $\mathrm{CO}_{3}^{2-}$ में सभी कार्बन-ऑक्सीजन बंध समतुल्य हैं। इसलिए कार्बोनेट आयन को नीचे दर्शाई गई I, II और III कैनोनिक रूपों के अनुनादी संकर के रूप में सर्वोत्तम रूप से वर्णित किया गया है।

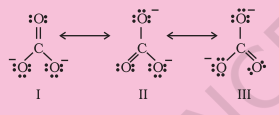
चित्र 4.4 $\mathrm{CO}_{3}^{2-}$ में अनुनाद, I, II और III तीनों कैनोनिक रूपों को दर्शाते हैं।

प्रश्न 4.4

$\mathrm{CO}_{2}$ अणु की संरचना समझाइए।

हल

प्रायोगिक रूप से निर्धारित $\mathrm{CO}_2$ में कार्बन से ऑक्सीजन बंध की लंबाई $115 \mathrm{pm}$ है। सामान्य कार्बन से ऑक्सीजन द्विबंध $(\mathrm{C}=\mathrm{O})$ और कार्बन से ऑक्सीजन त्रिबंध $(\mathrm{C} \equiv \mathrm{O})$ की लंबाइयाँ क्रमशः $121 \mathrm{pm}$ और $110 \mathrm{pm}$ हैं। $\mathrm{CO}_2$ में कार्बन-ऑक्सीजन बंध की लंबाई $(115 \mathrm{pm})$ $\mathrm{C}=\mathrm{O}$ और $\mathrm{C} \equiv \mathrm{O}$ दोनों के मानों के बीच स्थित है। स्पष्ट है कि एक अकेली लुइस संरचना इस स्थिति को दर्शा नहीं सकती और ऐसा करने के लिए एक से अधिक लुइस संरचनाएँ लिखना आवश्यक हो जाता है और यह मानना पड़ता है कि $\mathrm{CO}_2$ की संरचना को सर्वोत्तम रूप से I, II और III नामक मानक या अनुनाद रूपों के संकर के रूप में वर्णित किया जाता है।

आकृति 4.5 $\mathrm{CO}_{2}$ अणु में अनुनाद, I, II और III तीन मानक रूपों को दर्शाते हैं।

सामान्यतया, यह कहा जा सकता है कि

  • अनुनाद अणु को स्थिर करता है क्योंकि अनुनाद संकर की ऊर्जा किसी एकल मानक संरचना की ऊर्जा से कम होती है; और,
  • अनुनाद समग्र रूप से बंध की विशेषताओं का औसत निकालता है।

इस प्रकार $\mathrm{O}_{3}$ अनुनाद संकर की ऊर्जा दोनों मानक रूपों I और II (आकृति 4.3) की तुलना में कम होती है।

अनुनाद से जुड़ी कई गलत धारणाएँ हैं और उन्हें दूर करने की आवश्यकता है। आपको याद रखना चाहिए:

  • कैनोनिकल रूपों का कोई वास्तविक अस्तित्व नहीं होता।
  • अणु किसी निश्चित अंश के लिए एक कैनोनिकल रूप में और अन्य अंशों के लिए अन्य कैनोनिकल रूपों में नहीं रहता।
  • कैनोनिकल रूपों के बीच कोई ऐसा साम्यावस्था नहीं होता जैसा कि टॉटोमेरिज्म में टॉटोमेरिक रूपों (कीटो और इनॉल) के बीच होता है।
  • अणु का एक ही संरचना होती है जो कैनोनिकल रूपों का अनुनाद हाइब्रिड होता है और जिसे एक single Lewis संरचना द्वारा चित्रित नहीं किया जा सकता।

4.3.6 बॉन्ड की ध्रुवता

सौ प्रतिशत आयनिक या सहसंयोजक बॉन्ड का अस्तित्व एक आदर्श स्थिति को दर्शाता है। वास्तव में कोई भी बॉन्ड या यौगिक पूरी तरह से सहसंयोजक या आयनिक नहीं होता। दो हाइड्रोजन परमाणुओं के बीच सहसंयोजक बॉन्ड की स्थिति में भी कुछ आयनिक लक्षण होता है।

जब दो समान परमाणुओं के बीच सहसंयोजी बंध बनता है, उदाहरण के लिए $\mathrm{H}_2$, $\mathrm{O}_2$, $\mathrm{Cl}_2$, $\mathrm{~N}_2$ या $\mathrm{F}_2$ में, साझा किए गए इलेक्ट्रॉनों के युग्म को दोनों परमाणुओं द्वारा समान रूप से आकर्षित किया जाता है। परिणामस्वरूप इलेक्ट्रॉन युग्म दोनों समान नाभिकों के ठीक बीच स्थित होता है। इस प्रकार बना बंध अध्रुवीय सहसंयोजी बंध कहलाता है। इसके विपरीत, एक विषमपरमाणुक अणु जैसे $\mathrm{HF}$ के मामले में, दो परमाणुओं के बीच साझा किया गया इलेक्ट्रॉन युग्म फ्लोरीन की ओर अधिक विस्थापित हो जाता है क्योंकि फ्लोरीन की विद्युतऋणात्मकता (इकाई 3) हाइड्रोजन की तुलना में कहीं अधिक होती है। परिणामी सहसंयोजी बंध एक ध्रुवीय सहसंयोजी बंध होता है।

ध्रुवीकरण के परिणामस्वरूप, अणु में द्विध्रुव आघूर्ण होता है (नीचे चित्रित किया गया है) जिसे धनात्मक और ऋणात्मक आवेशों के केंद्रों के बीच की दूरी और आवेश की परिमाण के गुणनफल के रूप में परिभाषित किया जा सकता है। इसे आमतौर पर एक ग्रीक अक्षर ‘$\mu$’ द्वारा निर्दिष्ट किया जाता है। गणितीय रूप से इसे निम्नलिखित रूप में व्यक्त किया जाता है:

द्विध्रुव आघूर्ण $(\mu)=$ आवेश $(Q) \times$ पृथक्करण की दूरी $(\mathrm{r})$

द्विध्रुव आघूर्ण को आमतौर पर डेबाई इकाइयों (D) में व्यक्त किया जाता है। रूपांतरण कारक है

$$ 1 \mathrm{D}=3.33564 \times 10^{-30} \mathrm{C} \mathrm{m} $$

जहाँ $\mathrm{C}$ कूलॉम है और $\mathrm{m}$ मीटर है।

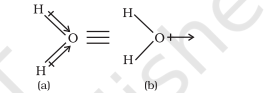
आगे डाइपोल आघूर्ण एक सदिश राशि है और परंपरा के अनुसार इसे एक छोटे तीर से दर्शाया जाता है जिसकी पूंछ ऋणात्मक केंद्र पर होती है और सिर धनात्मक केंद्र की ओर इशारा करता है। लेकिन रसायन विज्ञान में डाइपोल आघूर्ण की उपस्थिति को क्रॉस किए हुए तीर $(\rightarrow)$ से दर्शाया जाता है जिसे अणु की लूइस संरचना पर लगाया जाता है। क्रॉस धनात्मक सिरे पर होता है और तीर का सिरा ऋणात्मक सिरे पर होता है। उदाहरण के लिए HF का डाइपोल आघूर्ण इस प्रकार दर्शाया जा सकता है :

$$ \stackrel{+}{\mathrm{H} \longrightarrow} \underset{\because}{*}: $$

यह तीर अणु में इलेक्ट्रॉन घनत्व के स्थानांतरण की दिशा को दर्शाता है। ध्यान दें कि क्रॉस किए हुए तीर की दिशा डाइपोल आघूर्ण सदिश की परंपरागत दिशा के विपरीत होती है।

पीटर डेबाई, डच रसायनज्ञ ने 1936 में एक्स-रे विवर्तन और डाइपोल आघूर्ण पर अपने कार्य के लिए नोबेल पुरस्कार प्राप्त किया। डाइपोल आघूर्ण की परिमाण को डेबाई इकाइयों में दिया जाता है ताकि उन्हें सम्मान दिया जा सके।

बहुपरमाणुक अणुओं के मामले में द्विध्रुव आघूर्ण न केवल बंधों के व्यक्तिगत द्विध्रुव आघूर्णों — जिन्हें बंध द्विध्रुव कहा जाता है — पर निर्भर करता है, बल्कि अणु में विभिन्न बंधों की स्थानिक व्यवस्था पर भी निर्भर करता है। ऐसी स्थिति में, किसी अणु का द्विध्रुव आघूर्ण विभिन्न बंधों के द्विध्रुव आघूर्णों का सदिश योग होता है। उदाहरण के लिए, $\mathrm{H}_{2} \mathrm{O}$ अणु, जिसकी मुड़ी हुई संरचना है, दो $\mathrm{O}-\mathrm{H}$ बंध $104.5^{\circ}$ के कोण पर उन्मुख हैं। $6.17 \times 10^{-30} \mathrm{C} \mathrm{m}$ $(1 \mathrm{D} = 3.33564 \times 10^{-30} \mathrm{C} \mathrm{m})$ का निवल द्विध्रुव आघूर्ण दो $\mathrm{O}-\mathrm{H}$ बंधों के द्विध्रुव आघूर्णों का परिणामी है।

निवल द्विध्रुव आघूर्ण, $\mu=1.85 \mathrm{D}$

$=1.85 \times 3.33564 \times 10^{-30} \mathrm{C} \mathrm{m}=6.17 \times 10^{-30} \mathrm{C} \mathrm{m}$

$\mathrm{BeF}_{2}$ के मामले में द्विध्रुव आघूर्ण शून्य होता है। ऐसा इसलिए है क्योंकि दो समान बंध द्विध्रुव विपरीत दिशाओं में इंगित करते हैं और एक-दूसरे के प्रभाव को रद्द कर देते हैं।

चतुष्परमाणुक अणु में, उदाहरण के लिए (\mathrm{BF}_{3}) में, डाइपोल आघूर्ण शून्य होता है यद्यपि (\mathrm{B}-\mathrm{F}) आबंध एक-दूसरे से (120^{\circ}) के कोण पर स्थित हैं, तीनों आबंध आघूर्णों का कुल योग शून्य होता है क्योंकि किन्हीं दो का परिणामी तीसरे के समान और विपरीत होता है।

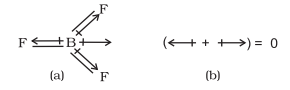
(\mathrm{BF}_3) अणु; (a) आबंध डाइपोलों और (b) कुल डाइपोल आघूर्ण का प्रतिनिधित्व

आइए $\mathrm{NH}_3$ और $\mathrm{NF}_3$ अणु का एक रोचक मामला पढ़ें। दोनों अणु नाइट्रोजन पर एकाकी इलेक्ट्रॉन युग्म के साथ पिरामिडी आकार रखते हैं। यद्यपि फ्लोरीन नाइट्रोजन से अधिक विद्युतऋणात्मक है, $\mathrm{NH}_3\left(4.90 \times 10^{-30} \mathrm{C} \mathrm{m}\right)$ का परिणामी द्विध्रुव आघूर्ण $\mathrm{NF}_3\left(0.8 \times 10^{-30} \mathrm{C} \mathrm{m}\right)$ से अधिक है। ऐसा इसलिए है क्योंकि $\mathrm{NH}_3$ में एकाकी युग्म के कारण कक्षक द्विध्रुव $\mathrm{N}-\mathrm{H}$ बंधों के परिणामी द्विध्रुव आघूर्ण की ही दिशा में होता है, जबकि $\mathrm{NF}_3$ में कक्षक द्विध्रुव तीनों N-F बंधों के परिणामी द्विध्रुव आघूर्ण की विपरीत दिशा में होता है। एकाकी युग्म के कारण उत्पन्न कक्षक द्विध्रुव परिणामी $\mathrm{N}-\mathrm{F}$ बंध आघूर्णों के प्रभाव को घटा देता है, जिससे $\mathrm{NF}_3$ का द्विध्रुव आघूर्ण नीचे दर्शाए अनुसार कम हो जाता है:

कुछ अणुओं के द्विध्रुव आघूर्ण तालिका 4.5 में दिखाए गए हैं।

जैसे सभी सहसंयोजी बंधों में कुछ आंशिक आयनिक लक्षण होता है, वैसे ही आयनिक बंधों में भी आंशिक सहसंयोजी लक्षण होता है। आयनिक बंधों के आंशिक सहसंयोजी लक्षण को फाजन्स ने निम्न नियमों के संदर्भ में चर्चित किया:

  • जितना छोटा धनायन का आकार होगा और ऋणायन का आकार बड़ा होगा, आयनिक बंध की सहसंयोजक प्रकृति उतनी ही अधिक होगी।
  • धनायन पर जितना अधिक आवेश होगा, आयनिक बंध की सहसंयोजक प्रकृति उतनी ही अधिक होगी।
  • समान आकार और आवेश वाले धनायनों में, वह जिसकी इलेक्ट्रॉनिक विन्यास $(n-1) d^{n} n s^{\circ}$ हो, जो संक्रमण धातुओं के लिए विशिष्ट है, उसकी ध्रुवण क्षमता उस धनायन से अधिक होती है जिसका दुर्लभ गैस विन्यास $n s^{2} n p^{6}$ हो, जो क्षार और क्षारीय पृथ्वी धातु धनायनों के लिए विशिष्ट है।

धनायन ऋणायन को ध्रुवित करता है, इलेक्ट्रॉनिक आवेश को अपनी ओर खींचता है और इस प्रकार दोनों के बीच इलेक्ट्रॉनिक आवेश बढ़ा देता है। यह वही है जो सहसंयोजक बंध में होता है, अर्थात् नाभिकों के बीच इलेक्ट्रॉन आवेश घनत्व का निर्माण। धनायन की ध्रुवण क्षमता, ऋणायन की ध्रुवणीयता और ऋणायन के विरूपण (ध्रुवण) की सीमा वे कारक हैं जो आयनिक बंध के प्रतिशत सहसंयोजक स्वभूत को निर्धारित करते हैं।

4.4 वैलेंस शैल इलेक्ट्रॉन युगल प्रतिकर्षण (VSEPR) सिद्धांत

जैसा कि पहले ही समझाया गया है, लुइस संकल्पना अणुओं के आकृतियों को समझाने में असमर्थ है। यह सिद्धांत सहसंयोजक अणुओं की आकृतियों को भविष्यवाणी करने की एक सरल प्रक्रिया प्रदान करता है। सिजविक और पॉवेल ने 1940 में एक सरल सिद्धांत प्रस्तावित किया जो परमाणुओं के वैलेंस शैल में इलेक्ट्रॉन युगलों की प्रतिकर्षी अन्योन्यक्रियाओं पर आधारित था। इसे नायहोम और गिलेस्पी (1957) ने और विकसित और पुनःपरिभाषित किया।

तालिका 4.5 चयनित अणुओं के द्विध्रुव आघूर्ण

अणु का प्रकार उदाहरण डाइपोल
आघूर्ण, $\boldsymbol{\mu}(\mathbf{D})$		 ज्यामिति
अणु $(\mathbf{A B})$ $\mathrm{HF}$ 1.78 रेखीय
$\mathrm{HCl}$ 1.07 रेखीय
$\mathrm{HBr}$ 0.79 रेखीय
$\mathrm{Hl}$ 0.38 रेखीय
$\mathrm{H}_{2}$ 0 रेखीय
अणु $\left(\mathbf{A B}_{\mathbf{2}}\right)$ $\mathrm{H}_{2} \mathrm{O}$ 1.85 वक्र
$\mathrm{H}_{2} \mathrm{~S}$ 0.95 वक्र
$\mathrm{CO}_{2}$ 0 रेखीय
अणु $\left(\mathbf{A B}_{3}\right)$ $\mathrm{NH}_{3}$ 1.47 त्रिकोणीय-पिरामिडी
$\mathrm{NF}_{3}$ 0.23 त्रिकोणीय-पिरामिडी
$\mathrm{BF}_{3}$ 0 त्रिकोणीय-समतली
अणु $\left(\mathbf{A B}_{\mathbf{4}}\right)$ $\mathrm{CH}_{4}$ 0 चतुष्फलकीय
$\mathrm{CHCl}_{3}$ 1.04 चतुष्फलकीय
$\mathrm{CCl}_{4}$ 0 चतुष्फलकीय

VSEPR सिद्धांत के मुख्य नियम इस प्रकार हैं:

  • किसी अणु का आकार उसके केंद्रीय परमाणु के वैलेन्स कोश के चारों ओर उपस्थित इलेक्ट्रॉन युग्मों (बंधित या अबंधित) की संख्या पर निर्भर करता है।
  • वैलेन्स कोश में उपस्थित इलेक्ट्रॉन युग्म एक-दूसरे को प्रतिकर्षित करते हैं क्योंकि उनके इलेक्ट्रॉन बादल ऋणात्मक आवेशित होते हैं।
  • ये इलेक्ट्रॉन युग्म अंतरिक्ष में ऐसे स्थान ग्रहण करने का प्रयास करते हैं जिससे प्रतिकर्षण न्यूनतम हो और उनके बीच की दूरी अधिकतम हो।
  • वैलेन्स कोश को एक गोले के रूप में लिया जाता है जिसकी सतह पर इलेक्ट्रॉन युग्म एक-दूसरे से अधिकतम दूरी पर स्थित होते हैं।
  • एक बहुबंध को एकल इलेक्ट्रॉन युग्म के समान माना जाता है और बहुबंध के दो या तीन इलेक्ट्रॉन युग्मों को एक ही सुपर युग्म माना जाता है।
  • जहाँ दो या अधिक अनुनाद संरचनाएँ किसी अणु को दर्शा सकती हैं, वहाँ VSEPR मॉडल उनमें से किसी भी संरचना पर लागू होता है।

इलेक्ट्रॉन युग्मों की प्रतिकर्षी अन्योन्यक्रिया निम्न क्रम में घटती है:

अकेला युग्म (lp) - अकेला युग्म (lp) > अकेला युग्म (lp) - बंध युग्म (bp) > बंध युग्म (bp) - बंध युग्म (bp)

निहोल्म और गिलेस्पी (1957) ने VSEPR मॉडल को परिष्कृत किया, जिसमें उन्होंने अकेले इलेक्ट्रॉन युग्मों और बंधनकारी इलेक्ट्रॉन युग्मों के बीच महत्वपूर्ण अंतर को समझाया। जबकि अकेले इलेक्ट्रॉन युग्म केंद्र पर स्थित परमाणु पर स्थानीयकृत होते हैं, प्रत्येक बंधनकारी युग्म दो परमाणुओं के बीच साझा किया जाता है। इसके परिणामस्वरूप, अणु में अकेले इलेक्ट्रॉन युग्म बंधनकारी इलेक्ट्रॉन युग्मों की तुलना में अधिक स्थान घेरते हैं। इससे अकेले इलेक्ट्रॉन युग्मों के बीच अधिक प्रतिकर्षण उत्पन्न होता है, जैसा कि अकेले युग्म-बंधन युग्म और बंधन युग्म-बंधन युग्म प्रतिकर्षणों की तुलना में होता है। ये प्रतिकर्षण प्रभाव अणुओं में आदर्श आकृतियों से विचलन और बंधन कोणों में परिवर्तन उत्पन्न करते हैं।

VSEPR सिद्धांत की सहायता से अणुओं की ज्यामितीय आकृतियों की भविष्यवाणी करने के लिए, अणुओं को दो श्रेणियों में विभाजित करना सुविधाजनक होता है: (i) वे अणु जिनमें केंद्र पर स्थित परमाणु पर कोई अकेला इलेक्ट्रॉन युग्म नहीं होता है, और (ii) वे अणु जिनमें केंद्र पर स्थित परमाणु पर एक या अधिक अकेले इलेक्ट्रॉन युग्म होते हैं।

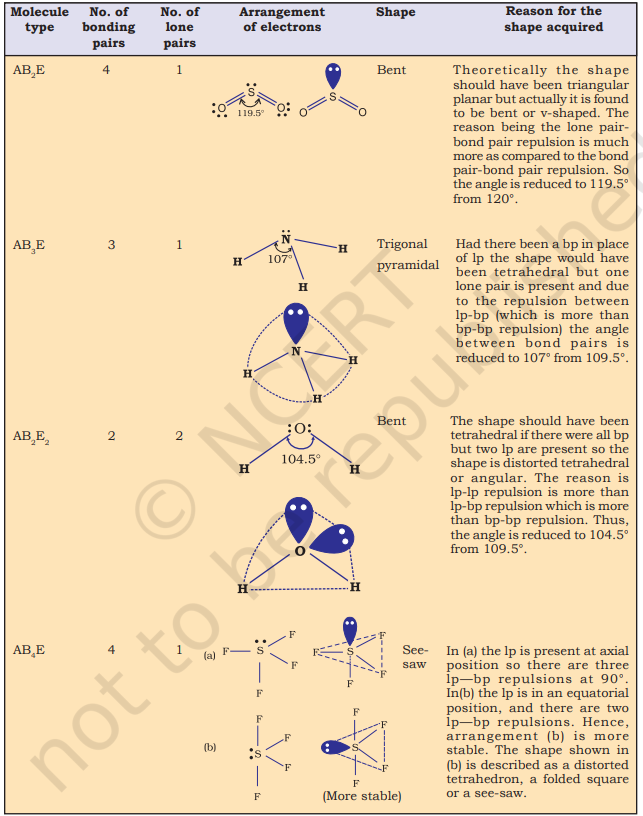
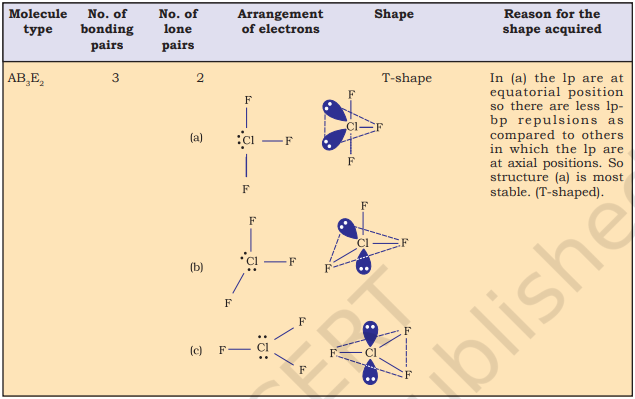
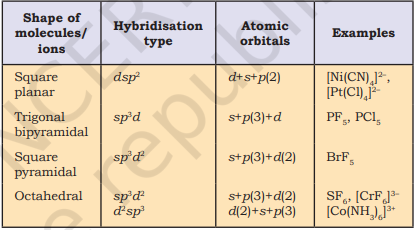
तालिका 4.6 (पृष्ठ 114) एक केंद्र पर स्थित परमाणु A (जिस पर कोई अकेला युग्म नहीं है) के चारों ओर इलेक्ट्रॉन युग्मों की व्यवस्था और AB प्रकार के कुछ अणुओं/आयनों की ज्यामितियाँ दिखाती है। तालिका 4.7 (पृष्ठ 115) कुछ सरल अणुओं और आयनों की आकृतियाँ दिखाती है जिनमें केंद्र पर स्थित परमाणु पर एक या अधिक अकेले इलेक्ट्रॉन युग्म होते हैं। तालिका 4.8 (पृष्ठ 116) अणु की ज्यामिति में विरूपण के कारणों की व्याख्या करती है।

जैसा कि तालिका 4.6 में दिखाया गया है, $\mathrm{AB}_2, \mathrm{AB}_3, \mathrm{AB}_4, \mathrm{AB}_5$ और $\mathrm{AB}_6$ यौगिकों में, केंद्र पर स्थित परमाणु A के चारों ओर इलेक्ट्रॉन युग्मों और B परमाणुओं की व्यवस्था क्रमशः रैखिक, त्रिकोणीय समतलीय, चतुष्फलकीय, त्रिकोणीय द्विपिरामिडीय और अष्टफलकीय होती है। इस प्रकार की व्यवस्था $\mathrm{BF}_3\left(\mathrm{AB}_3\right), \mathrm{CH}_4\left(\mathrm{AB}_4\right)$ और $\mathrm{PCl}_5\left(\mathrm{AB}_5\right)$ जैसे अणुओं में उनके गेंद-छड़ मॉडलों द्वारा नीचे दिखाई गई है।

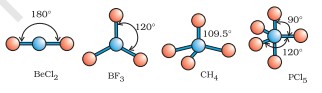
आकृति 4.8 वे अणु आकृतियाँ जिनमें केंद्रीय परमाणु पर कोई एकाकी युग्म नहीं है

VSEPR सिद्धांत बड़ी संख्या में अणुओं, विशेषकर $p$-ब्लॉक तत्वों के यौगिकों की ज्यामिति को सटीक रूप से भविष्यवाणी करने में सक्षम है। यह संभावित संरचनाओं के बीच ऊर्जा अंतर बहुत कम होने पर भी ज्यामिति को काफी सटीकता से निर्धारित करने में काफी सफल है। VSEPR सिद्धांत का सैद्धांतिक आधार, ज्यामितीय आकृतियों पर इलेक्ट्रॉन युग्म प्रतिकर्षणों के प्रभावों के संदर्भ में, स्पष्ट नहीं है और यह संदेह तथा चर्चा का विषय बना हुआ है।

तालिका 4.6 वे अणु ज्यामितियाँ जिनमें केंद्रीय परमाणु पर कोई एकाकी इलेक्ट्रॉन युग्म नहीं है

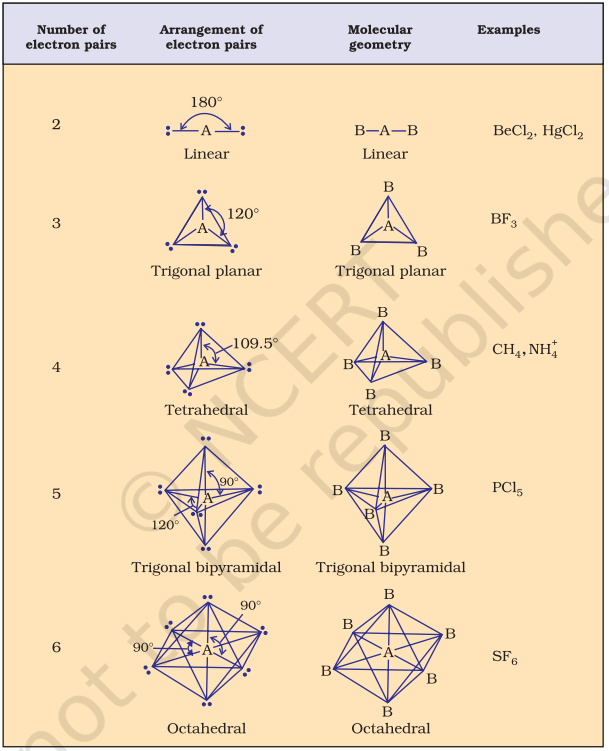
तालिका 4.7 कुछ सरल अणुओं/आयनों की आकृति (ज्यामिति) जिनके केंद्रीय आयनों में इलेक्ट्रॉनों (E) के एक या अधिक एकाकी युग्म होते हैं

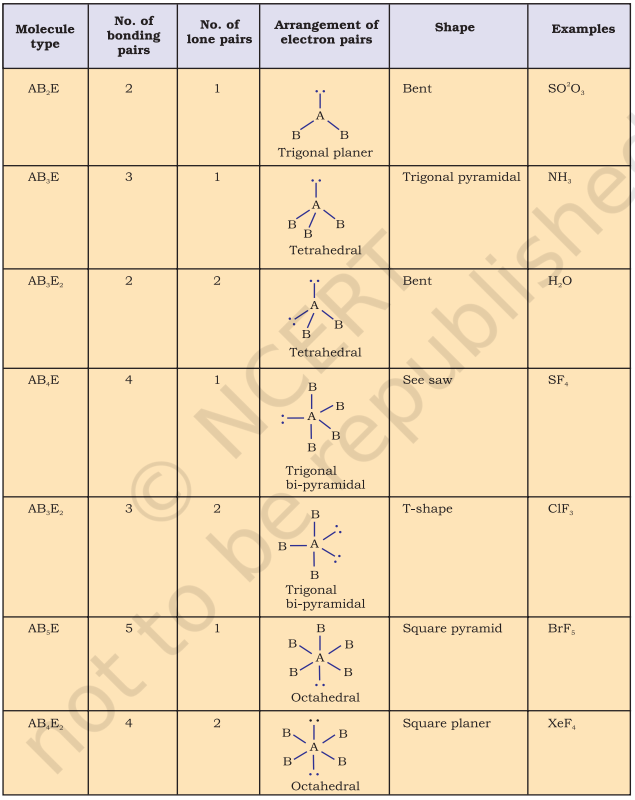
तालिका 4.8 बंध युग्म और एकाकी युग्म युक्त अणुओं की आकृतियाँ

4.5 संयोजक बंध सिद्धांत

जैसा कि हम जानते हैं कि लुईस दृष्टिकोण अणुओं की संरचना लिखने में मदद करता है लेकिन यह रासायनिक बंध के निर्माण की व्याख्या करने में विफल रहता है। यह $\mathrm{H}_2(435.8 \mathrm{~kJ}$ $\left.\mathrm{mol}^{-1}, 74 \mathrm{pm}\right)$ और $\mathrm{F}_2\left(155 \mathrm{~kJ} \mathrm{~mol}^{-1}, 144 \mathrm{pm}\right)$ जैसे अणुओं में बंध विघटन एन्थैल्पी और बंध लंबाई में अंतर के लिए कोई कारण नहीं देता है, यद्यपि दोनों ही स्थितियों में संबंधित परमाणुओं के बीच एक इलेक्ट्रॉन युग्म के साझाकरण से एक एकल सहसंयोजक बंध बनता है। यह बहुपरमाणुक अणुओं के आकृतियों के बारे में भी कोई विचार नहीं देता है।

इसी प्रकार VSEPR सिद्धांत सरल अणुओं की ज्यामिति देता है लेकिन सैद्धांतिक रूप से इसकी व्याख्या नहीं करता है और इसके सीमित अनुप्रयोग भी हैं। इन सीमाओं को दूर करने के लिए क्वांटम यांत्रिक सिद्धांतों पर आधारित दो महत्वपूर्ण सिद्धांत प्रस्तुत किए गए हैं। ये हैं वैलेंस बंध (VB) सिद्धांत और आण्विक कक्षक (MO) सिद्धांत।

वैलेंस बॉन्ड सिद्धांत को हाइटलर और लंदन (1927) ने प्रस्तुत किया और इसे पॉलिंग तथा अन्य लोगों ने आगे विकसित किया। वैलेंस बॉन्ड सिद्धांत की चर्चा परमाणु कक्षकों, तत्वों के इलेक्ट्रॉनिक विन्यास (इकाई 2), परमाणु कक्षकों के ओवरलैप मानदंड, परमाणु कक्षकों के संकरण और विचलन तथा अतिव्यापन के सिद्धांतों के ज्ञान पर आधारित है। इन पहलुओं के संदर्भ में VB सिद्धांत का कठोर उपचार इस पुस्तक की सीमा से परे है। इसलिए सुविधा के लिए, वैलेंस बॉन्ड सिद्धांत की चर्चा केवल गुणात्मक और गैर-गणितीय उपचार के संदर्भ में की गई है। शुरुआत के लिए, आइए हाइड्रोजन अणु के निर्माण पर विचार करें जो सभी अणुओं में सबसे सरल है।

दो हाइड्रोजन परमाणु A और B को विचारें जो एक-दूसरे के पास आ रहे हैं, जिनके नाभिक $\mathrm{N}_{\mathrm{A}}$ और $N_B$ हैं और उनमें उपस्थित इलेक्ट्रॉनों को $e_A$ और $e_B$ द्वारा दर्शाया गया है। जब दो परमाणु एक-दूसरे से बहुत दूरी पर होते हैं, तब उनके बीच कोई अन्योन्यक्रिया नहीं होती है। जैसे ही ये दो परमाणु एक-दूसरे के पास आते हैं, नई आकर्षण और प्रतिकर्षण बल कार्य करने लगते हैं।

आकर्षण बल उत्पन्न होते हैं:

(i) एक परमाणु के नाभिक और उसके अपने इलेक्ट्रॉन के बीच, अर्थात् $N_{A}-e_{A}$ और $N_{B}-e_{B}$।

(ii) एक परमाणु के नाभिक और दूसरे परमाणु के इलेक्ट्रॉन के बीच, अर्थात् $N_{A}-e_{B}, N_{B}-e_{A}$।

इसी प्रकार प्रतिकर्षण बल उत्पन्न होते हैं

(i) दो परमाणुओं के इलेक्ट्रॉनों के बीच, जैसे $e_{A}-e_{B}$,

(ii) दो परमाणुओं के नाभिकों के बीच $N_{A}-N_{B}$।

आकर्षण बल दो परमाणुओं को एक-दूसरे के निकट लाने का प्रयास करते हैं जबकि प्रतिकर्षण बल उन्हें अलग धकेलने का प्रयास करते हैं (चित्र 4.7)।

चित्र 4.7 H₂ अणु के निर्माण के दौरान आकर्षण और प्रतिकर्षण बल

प्रायोगिक रूप से यह पाया गया है कि नए आकर्षण बल का परिमाण नए प्रतिकर्षण बलों से अधिक होता है। परिणामस्वरूप, दो परमाणु एक-दूसरे के निकट आते हैं और स्थितिज ऊर्जा घटती है। अंततः एक ऐसा चरण आता है जहां कुल आकर्षण बल प्रतिकर्षण बल को संतुलित करता है और तंत्र न्यूनतम ऊर्जा प्राप्त करता है। इस चरण पर दो हाइड्रोजन परमाणुओं को एक स्थिर अणु बनाने के लिए आबद्ध माना जाता है जिसकी बंध लंबाई 74 pm है।

चूंकि दो हाइड्रोजन परमाणुओं के बीच बंध बनने पर ऊर्जा मुक्त होती है, हाइड्रोजन अणु अलग-थलग हाइड्रोजन परमाणुओं की तुलना में अधिक स्थिर होता है। इस प्रकार मुक्त होने वाली ऊर्जा को बंध एन्थैल्पी कहा जाता है, जो चित्र 4.8 में दर्शाए गए वक्र के न्यूनतम बिंदु के अनुरूप होती है। इसके विपरीत, H₂ अणु के एक मोल को विघटित करने के लिए 435.8 kJ ऊर्जा की आवश्यकता होती है।

H₂(g) + 435.8 kJ mol⁻¹ → H(g) + H(g)

आकृति 4.8 H परमाणुओं के अंतर-न्यूक्लीय दूरी के फलन के रूप में H₂ अणु के निर्माण के लिए स्थितिज ऊर्जा वक्र। वक्र में न्यूनतम H₂ की सबसे स्थिर अवस्था के अनुरूप होता है।

4.5.1 कक्षीय ओवरलैप संकल्पना

हाइड्रोजन अणु के निर्माण में एक न्यूनतम ऊर्जा अवस्था तब आती है जब दो हाइड्रोजन परमाणु इतने निकट होते हैं कि उनकी परमाण्वीय कक्षाएँ आंशिक रूप से आपस में घुल-मिल जाती हैं। परमाण्वीय कक्षाओं के इस आंशिक मिलन को परमाण्वीय कक्षाओं का ओवरलैप कहा जाता है जिससे इलेक्ट्रॉनों की युग्मन होता है। ओवरलैप की मात्रा एक सहसंयोजी बंधन की ताकत निर्धारित करती है। सामान्यतः, जितना अधिक ओवरलैप होता है, उतना ही मजबूत बंधन दो परमाणुओं के बीच बनता है। इसलिए, कक्षीय ओवरलैप संकल्पना के अनुसार, दो परमाणुओं के बीच सहसंयोजी बंधन का निर्माण उनके संयोजक कोश में उपस्थित विपरीत स्पिन वाले इलेक्ट्रॉनों के युग्मन से होता है।

4.5.2 बंधनों की दिशात्मक विशेषताएँ

जैसा कि हम पहले ही देख चुके हैं, सहसंयोजी बंधन परमाण्वीय कक्षाओं के ओवरलैप से बनता है। हाइड्रोजन का अणु दो H परमाणुओं की 1s-कक्षाओं के ओवरलैप के कारण बनता है।

बहुपरमाण्विक अणुओं जैसे CH₄, NH₃ और H₂O के मामले में, बंधन निर्माण के अतिरिक्त अणुओं की ज्यामिति भी महत्वपूर्ण होती है। उदाहरण के लिए ऐसा क्यों है कि CH₄ अणु का आकार चतुष्फलकीय होता है और HCH बंधन कोण 109.5° होते हैं? NH₃ अणु का आकार पिरामिडनुमा क्यों होता है?

वैलेंस बॉन्ड सिद्धांत बहुपरमाणुक अणुओं जैसे (\mathrm{CH}_4), (\mathrm{NH}_3) और (\mathrm{H}_2 \mathrm{O}) आदि में बंधन की आकृति, निर्माण और दिशात्मक गुणों को परमाण्वीय कक्षकों के ओवरलैप और संकरण के संदर्भ में समझाता है।

4.5.3 परमाण्वीय कक्षकों का ओवरलैपिंग

जब दो परमाणुओं की कक्षाएँ बंध बनाने के लिए निकट आती हैं, तो उनका ओवरलैप सकारात्मक, नकारात्मक या शून्य हो सकता है, जो कक्षीय तरंग फलन के आयाम के चिह्न (फेज़) और दिशा के अभिविन्यास पर निर्भर करता है (चित्र 4.9)। चित्र 4.9 में सीमा सतह आरेखों पर सकारात्मक और नकारात्मक चिह्न कक्षीय तरंग फलन के चिह्न (फेज़) को दर्शाते हैं और आवेश से संबंधित नहीं हैं। बंध बनाने वाली कक्षाओं का अंतरिक्ष में समान चिह्न (फेज़) और अभिविन्यास होना चाहिए। इसे सकारात्मक ओवरलैप कहा जाता है। $s$ और $p$ कक्षाओं के विभिन्न ओवरलैप चित्र 4.9 में दिखाए गए हैं।

ओवरलैप का मानदंड, जो सहसंयोजक बंधों के निर्माण का मुख्य कारक है, समरूप/विषमरूप द्विपरमाणुक अणुओं और बहुपरमाणुक अणुओं पर समान रूप से लागू होता है। हम जानते हैं कि (\mathrm{CH}_4), (\mathrm{NH}_3) और (\mathrm{H}_2 \mathrm{O}) अणुओं की आकृतियाँ क्रमशः चतुष्फलकीय, पिरामिडाकार और मुड़ी हुई हैं। इसलिए यह रोचक होगा कि VB सिद्धांत का उपयोग करके यह जानने की कोशिश की जाए कि क्या इन ज्यामितीय आकृतियों को कक्षीय ओवरलैप के संदर्भ में समझाया जा सकता है।

आइए पहले $CH_4$ (मीथेन) अणु पर विचार करें। कार्बन का इलेक्ट्रॉनिक विन्यास इसके आधारभूत अवस्था में $[\mathrm{He}] 2 s^2 2 p^2$ है, जो उत्तेजित अवस्था में $[\mathrm{He}] 2 s^1 2 p_{\mathrm{x}}^1$ $2 p_{\mathrm{y}}^1$ $2 p_z^1$ हो जाता है। इस उत्तेजना के लिए आवश्यक ऊर्जा कार्बन और हाइड्रोजन के कक्षकों के अतिव्यापन के कारण ऊर्जा के विमोचन से संतुलित हो जाती है।

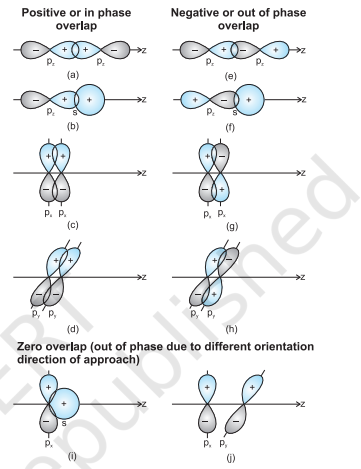
आकृति 4.9 s और p परमाण्विक कक्षकों के धनात्मक, ऋणात्मक और शून्य अतिव्यापन

कार्बन के चार परमाण्वीय कक्षक, प्रत्येक में एक अयुग्मित इलेक्ट्रॉन, चार H परमाणुओं के 1 s कक्षकों से ओवरलैप कर सकते हैं जो भी एक-एक इलेक्ट्रॉन से युक्त हैं। इससे चार C-H बंध बनेंगे। यह देखा जाएगा कि जबकि कार्बन के तीन p कक्षक परस्पर 90° पर होते हैं, इनके लिए HCH कोण भी 90° होगा। अर्थात् तीन C-H बंध परस्पर 90° पर उन्मुख होंगे। कार्बन का 2 s कक्षक और H का 1 s कक्षक गोलाकार सममित हैं और वे किसी भी दिशा में ओवरलैप कर सकते हैं। इसलिए चौथे C-H बंध की दिशा निर्धारित नहीं की जा सकती। यह विवरण 109.5° के चतुष्फलकीय HCH कोणों से मेल नहीं खाता। स्पष्ट है कि सरल परमाण्वीय कक्षक ओवरलैप CH₄ में बंधों की दिशात्मक विशेषताओं की व्याख्या नहीं करता। इसी प्रक्रिया और तर्कों से यह देखा जा सकता है कि NH₃ और H₂O अणुओं के मामले में HNH और HOH कोण 90° होने चाहिए। यह NH₃ और H₂O अणुओं में क्रमशः 107° और 104.5° के वास्तविक बंध कोणों से असहमति है।

4.5.4 ओवरलैपिंग के प्रकार और सहसंयोजी बंधों की प्रकृति

सहसंयोजी बंध को ओवरलैपिंग के प्रकार के आधार पर दो प्रकारों में वर्गीकृत किया जा सकता है:

(i) सिग्मा (σ) बंध, और (ii) पाई (π) बंध

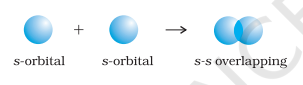
(i) सिग्मा (σ) बंध: इस प्रकार का सहसंयोजी बंध बंधन कक्षकों के अंत से अंत तक (सिर से सिर) ओवरलैप द्वारा अंतराभिकीय अक्ष के साथ बनता है। इसे सिर से सिर ओवरलैप या अक्षीय ओवरलैप कहा जाता है। यह परमाणु कक्षकों के निम्नलिखित प्रकारों में से किसी एक संयोजन द्वारा बनाया जा सकता है।

  • s-s ओवरलैपिंग: इस स्थिति में, दो अर्ध-भरे s-कक्षकों का अंतराभिकीय अक्ष के साथ ओवरलैप होता है जैसा कि नीचे दिखाया गया है:
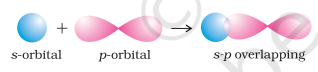
  • s-p ओवरलैपिंग: इस प्रकार का ओवरलैप एक परमाणु के अर्ध-भरे s-कक्षक और दूसरे परमाणु के अर्ध-भरे p-कक्षक के बीच होता है।
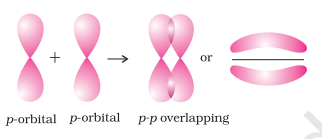
  • p-p ओवरलैपिंग: इस प्रकार का ओवरलैप दो निकट आ रहे परमाणुओं के अर्ध-भरे p-कक्षकों के बीच होता है।

(ii) pi( $\pi$ ) बंध : $\pi$ बंध के निर्माण में परमाण्वीय कक्षक इस प्रकार अतिव्यापन करते हैं कि उनके अक्ष एक-दूसरे के समानांतर और अंतराभिकीय अक्ष के लंबवत् रहते हैं। पार्श्व अतिव्यापन से बने कक्षक भाग ले रहे परमाणुओं के तल के ऊपर और नीचे दो सॉसर-प्रकार के आवेशित बादलों से बने होते हैं।

4.5.5 सिग्मा और pi बंधों की ताकत

मूलतः किसी बंध की ताकत अतिव्यापन की मात्रा पर निर्भर करती है। सिग्मा बंध में कक्षकों का अतिव्यापन अधिक मात्रा में होता है, इसलिए यह pi बंध की तुलना में अधिक मजबूत होता है, जिसमें अतिव्यापन कम मात्रा में होता है। यह भी ध्यान देना महत्वपूर्ण है कि किसी अणु के दो परमाणुओं के बीच एकाधिक बंध बनने पर sigma बंध के अतिरिक्त pi बंध भी बनता है।

4.6 संकरण

बहुपरमाणुक अणुओं जैसे (\mathrm{CH}_4), (\mathrm{NH}_3) और (\mathrm{H}_2\mathrm{O}) आदि की विशिष्ट ज्यामितीय आकृतियों को समझाने के लिए, पॉलिंग ने संकरण (hybridisation) की अवधारणा प्रस्तुत की। उनके अनुसार, परमाण्वीय कक्षिकाएं मिलकर नई समतुल्य कक्षिकाओं के समूह का निर्माण करती हैं, जिन्हें संकर कक्षिकाएं (hybrid orbitals) कहा जाता है। शुद्ध कक्षिकाओं के विपरीत, संकर कक्षिकाएं आबंध निर्माण में प्रयुक्त होती हैं। इस घटना को संकरण कहा जाता है, जिसे इस प्रकार परिभाषित किया जा सकता है: थोड़े भिन्न ऊर्जाओं की कक्षिकाओं के मिश्रण की प्रक्रिया, जिससे उनकी ऊर्जाओं का पुनर्वितरण होता है और समान ऊर्जा तथा आकृति की नई कक्षिकाओं का निर्माण होता है। उदाहरण के लिए, जब कार्बन की एक (2s) और तीन (2p)-कक्षिकाएं संकरित होती हैं, तो चार नई (sp^3) संकर कक्षिकाओं का निर्माण होता है।

संकरण की प्रमुख विशेषताएं: संकरण की मुख्य विशेषताएं निम्नलिखित हैं:

1. संकर कक्षिकाओं की संख्या उन परमाण्वीय कक्षिकाओं की संख्या के बराबर होती है जो संकरित होती हैं।

2. संकरित कक्षिकाएं सदैव ऊर्जा और आकृति में समतुल्य होती हैं।

3. संकर कक्षिकाएं शुद्ध परमाण्वीय कक्षिकाओं की तुलना में स्थायी आबंध बनाने में अधिक प्रभावी होती हैं।

4. ये संकर कक्षिकाएं स्थान में कुछ विशिष्ट दिशाओं में निर्देशित होती हैं ताकि इलेक्ट्रॉन युगलों के बीच न्यूनतम प्रतिकर्षण हो और एक स्थायी व्यवस्था बने। इसलिए, संकरण का प्रकार अणुओं की ज्यामिती को दर्शाता है।

संकरण के लिए महत्वपूर्ण शर्तें

(i) परमाणु की संयोजक कोश में उपस्थित कक्षक संकरित होते हैं।

(ii) संकरण से गुजरने वाले कक्षकों की ऊर्जा लगभग समान होनी चाहिए।

(iii) संकरण से पूर्व इलेक्ट्रॉन का प्रचालन आवश्यक शर्त नहीं है।

(iv) यह आवश्यक नहीं है कि केवल आधे भरे हुए कक्षक ही संकरण में भाग लें। कुछ स्थितियों में संयोजक कोश के भरे हुए कक्षक भी संकरण में भाग लेते हैं।

4.6.1 संकरण के प्रकार

$s, p$ और $d$ कक्षकों को सम्मिलित करने वाले विभिन्न प्रकार के संकरण होते हैं। विभिन्न प्रकार के संकरण निम्नलिखित हैं:

(I) sp संकरण: इस प्रकार के संकरण में एक $s$ और एक $p$ कक्षक के मिश्रण से दो समतुल्य $s p$ संकर कक्षक बनते हैं। यदि संकर कक्षकों को $z$-अक्ष के अनुदिश होना है, तो $s p$ संकरण के लिए उपयुक्त कक्षक $s$ और $p_{z}$ हैं। प्रत्येक $s p$ संकर कक्षक में 50 % s-प्रकृति और 50 % p-प्रकृति होती है। ऐसा अणु जिसमें केंद्रीय परमाणु $s p$-संकरित हो और सीधे दो अन्य केंद्रीय परमाणुओं से जुड़ा हो, रेखीय ज्यामिति रखता है। इस प्रकार के संकरण को विकर्ण संकरण भी कहा जाता है।

दो $s p$ संकर $z$-अक्ष के विपरीत दिशाओं में इंगित करते हैं, जिनमें सकारात्मक लोब उभरे हुए होते हैं और अत्यंत लघु नकारात्मक लोब होते हैं, जो अधिक प्रभावी ओवरलैपिंग प्रदान करते हैं जिससे प्रबल आबंध बनते हैं।

$s p$ संकरण वाले अणु का उदाहरण

$\mathbf{B e C l}_{2}$ : बेरीलियम की आधारभूत अवस्था की इलेक्ट्रॉनिक विन्यास $1 s^{2} 2 s^{2}$ है। उत्तेजित अवस्था में, द्वित्व (bivalency) को समझाने के लिए एक $2 \mathrm{~s}$-इलेक्ट्रॉन को रिक्त $2 p$ कक्षक में प्रवर्धित किया जाता है। एक $2 s$ और एक $2 p$-कक्षक संकरित होकर दो $s p$ संकरित कक्षक बनाते हैं। ये दोनों $s p$ संकर कक्षक विपरीत दिशाओं में 180° के कोण पर उन्मुख होते हैं। प्रत्येक $s p$ संकरित कक्षक क्लोरीन के $2 p$-कक्षक से अक्षतः ओवरलैप करके दो Be$\mathrm{Cl}$ सिग्मा बंध बनाता है। यह आकृति 4.10 में दिखाया गया है।

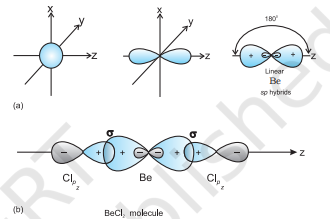
आकृति 4.10 (a) s और p कक्षकों से sp संकरों का निर्माण; (b) रेखीय $BeCl_2$ अणु का निर्माण

(II) $\boldsymbol{s p}^{2}$ संकरण : इस संकरण में तीन समतुल्य $s p^{2}$ संकरित कक्षक बनाने के लिए एक $s$ और दो $p$-कक्षकों की भागीदारी होती है। उदाहरण के लिए, $\mathrm{BCl} _{3}$ अणु में केंद्रीय बोरॉन परमाणु की भूमि अवस्था इलेक्ट्रॉनिक विन्यास $1 s^{2} 2 s^{2} 2 p^{1}$ है। उत्तेजित अवस्था में, $2 s$ के एक इलेक्ट्रॉन को रिक्त $2 p$ कक्षक में उत्प्रेरित किया जाता है, जिससे बोरॉन के पास तीन अयुग्मित इलेक्ट्रॉन हो जाते हैं। ये तीन कक्षक (एक $2 s$ और दो $2 p$) संकरित होकर तीन $s p^{2}$ संकर कक्षक बनाते हैं। इस प्रकार बने तीन संकर कक्षक त्रिकोणीय समतलीय व्यवस्था में उन्मुख होते हैं और क्लोरीन के $2 p$ कक्षकों से अतिव्यापन कर तीन $\mathrm{B}-\mathrm{Cl}$ आबंध बनाते हैं। इसलिए, $\mathrm{BCl} _{3}$ (चित्र 4.11) में ज्यामिति त्रिकोणीय समतलीय है जिसमें $\mathrm{ClBCl}$ आबंध कोण $120^{\circ}$ है।

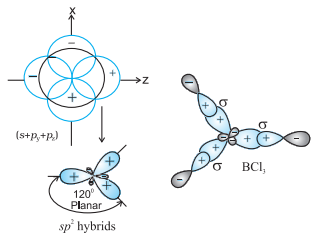
चित्र 4.11 $sp_2$ संकरों और $BCl_3$ अणु का निर्माण

(III) $\boldsymbol{s p}^{3}$ संकरण: इस प्रकार के संकरण को $\mathrm{CH}_{4}$ अणु के उदाहरण से समझाया जा सकता है जिसमें संयोजी कोश के एक s-कक्षक और तीन $p$-कक्षकों के मिश्रण से चार $s p^{3}$ संकर कक्षक समान ऊर्जा और आकृति के बनते हैं। प्रत्येक $s p^{3}$ संकर कक्षक में $25 % s$-प्रकृति और $75 % p$-प्रकृति होती है। इस प्रकार बने चारों $s p^{3}$ संकर कक्षक चतुष्फलक के चारों कोनों की ओर निर्देशित होते हैं। $s p^{3}$ संकर कक्षकों के बीच का कोण $109.5^{\circ}$ होता है जैसा कि चित्र 4.12 में दिखाया गया है।

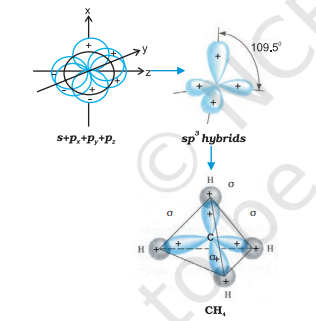
चित्र 4.12 कार्बन के s, $p_x$, $p_y$ और $p_z$ परमाणु कक्षकों के संयोजन से sp3 संकरों का निर्माण और $CH_4$ अणु का निर्माण

$\mathrm{NH}_3$ और $\mathrm{H}_2 \mathrm{O}$ अणुओं की संरचना को भी $s p^{3}$ संकरण की सहायता से समझाया जा सकता है। $\mathrm{NH}_3$ में, नाइट्रोजन की भूमिका अवस्था में संयोजक कोश (बाह्य) इलेक्ट्रॉनिक विन्यास $2 S^{2} 2 p_x^{1} 2 p_y^{1} 2 p_z^{1}$ होता है, जिसमें $s p^{3}$ संकर कक्षकों में तीन अयुग्मित इलेक्ट्रॉन होते हैं और चौथे में एक एकाकी इलेक्ट्रॉन युग्म होता है। ये तीन संकर कक्षक हाइड्रोजन अणुओं के $1 \mathrm{~s}$ कक्षकों से अतिव्यापन कर तीन $\mathrm{N}-\mathrm{H}$ सिग्मा बंध बनाते हैं। हम जानते हैं कि एकाकी युग्म और बंध युग्म के बीच प्रतिकर्षण बल, दो बंध युग्मों के बीच के प्रतिकर्षण बल से अधिक होता है। इस प्रकार अणु विकृत हो जाता है और बंध कोण $109.5^{\circ}$ से घटकर $107^{\circ}$ हो जाता है। ऐसे अणु की ज्यामिति पिरामिडी होगी जैसा कि चित्र 4.13 में दिखाया गया है।

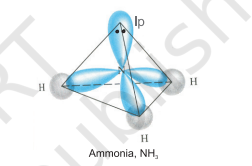
चित्र 4.13 $NH_3$ अणु का निर्माण

$\mathrm{H}_{2} \mathrm{O}$ अणु की स्थिति में, चार ऑक्सीजन कक्षक (एक $2 s$ और तीन $2 p$) $s p^{3}$ संकरण से गुजरते हैं, जिससे चार $s p^{3}$ संकर कक्षक बनते हैं, जिनमें से दो में एक-एक इलेक्ट्रॉन होता है और अन्य दो में इलेक्ट्रॉनों का एक युग्म होता है। ये चारों $s p^{3}$ संकर कक्षक एक चतुष्फलकीय ज्यामिति ग्रहण करते हैं, जिसके दो कोने हाइड्रोजन परमाणुओं से और अन्य दो एकाकी इलेक्ट्रॉन युग्मों से अधिग्रहित होते हैं। इस स्थिति में बंधन कोण $109.5^{\circ}$ से घटकर $104.5^{\circ}$ हो जाता है (चित्र 4.14) और इस प्रकार अणु V-आकृति या कोणीय ज्यामिति ग्रहण करता है।

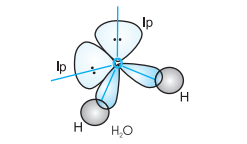
चित्र 4.14 $H_2 O$ अणु का निर्माण

4.6.2 $s p^{3}, s p^{2}$ और $s p$ संकरण के अन्य उदाहरण

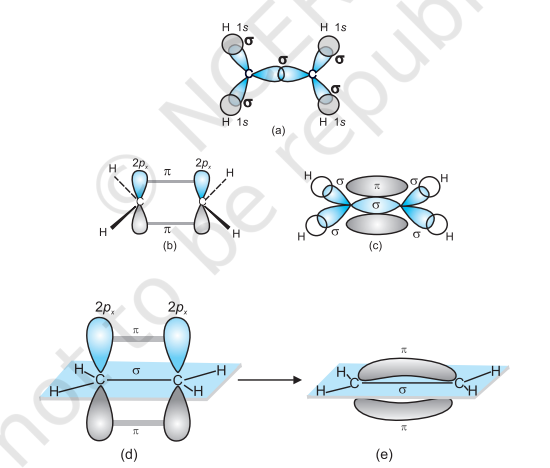
$\mathrm{C}_2 \mathrm{H}_6$ अणु में $s p^{3}$ संकरण: एथेन अणु में दोनों कार्बन परमाणु $s p^{3}$ संकर अवस्था ग्रहण करते हैं। कार्बन परमाणु के चार $s p^{3}$ संकर कक्षकों में से एक अक्षतः दूसरे परमाणु के समान कक्षक से ओवरलैप करके $s p^{3}-s p^{3}$ सिग्मा बंध बनाता है, जबकि प्रत्येक कार्बन परमाणु के अन्य तीन संकर कक्षक हाइड्रोजन परमाणुओं के साथ $s p^{3}-s$ सिग्मा बंध बनाने में प्रयुक्त होते हैं जैसा कि खंड 4.6.1(iii) में चर्चा किया गया है। इसलिए एथेन में $\mathrm{C}-\mathrm{C}$ बंध लंबाई 154 $\mathrm{pm}$ है और प्रत्येक $\mathrm{C}-\mathrm{H}$ बंध लंबाई $109 \mathrm{pm}$ है।

$\boldsymbol{s p}^{2}$ संकरण $\mathbf{C}_2 \boldsymbol{H}_4$ में: एथीन अणु के निर्माण में, कार्बन परमाणु के $s p^2$ संकरित कक्षकों में से एक कक्षक दूसरे कार्बन परमाणु के $s p^2$ संकरित कक्षक से अक्षीय रूप से ओवरलैप करता है ताकि $\mathrm{C}-\mathrm{C}$ सिग्मा बंध बन सके। जबकि प्रत्येक कार्बन परमाणु के शेष दो $s p^{2}$ संकरित कक्षक दो हाइड्रोजन परमाणुओं के साथ $s p^2-s$ सिग्मा बंध बनाने में प्रयुक्त होते हैं। एक कार्बन परमाणु का असंकरित कक्षक ($2 p_x$ या $2 p_y$) दूसरे कार्बन परमाणु के समान कक्षक के साथ पार्श्विक रूप से ओवरलैप करता है ताकि एक दुर्बल $\pi$ बंध बन सके, जिसमें दो समान इलेक्ट्रॉन बादल होते हैं जो कार्बन और हाइड्रोजन परमाणुओं के तल के ऊपर और नीचे वितरित होते हैं।

इस प्रकार, एथीन अणु में, कार्बन-कार्बन बंध में एक $s p^{2}-s p^{2}$ सिग्मा बंध और एक पाई $(\pi)$ बंध होता है जो $p$ कक्षकों के बीच होता है जो संकरण में प्रयुक्त नहीं होते और अणु के तल के लंबवत होते हैं; बंध लंबाई $134 \mathrm{pm}$ है। $\mathrm{C}-\mathrm{H}$ बंध $s p^{2}-\mathrm{s}$ सिग्मा है जिसकी बंध लंबाई $108 \mathrm{pm}$ है। $\mathrm{H}-\mathrm{C}-\mathrm{H}$ बंध कोण $117.6^{\circ}$ है जबकि $\mathrm{H}-\mathrm{C}-\mathrm{C}$ कोण $121^{\circ}$ है। एथीन में सिग्मा और पाई बंधों का निर्माण चित्र 4.15 में दिखाया गया है।

चित्र 4.15 इथीन में सिग्मा और पाई बंधों का निर्माण

$\mathbf{C}_2 \mathbf{H}_2$ में sp संकरण: एथाइन अणु के निर्माण में, दोनों कार्बन परमाणु sp-संकरण से गुजरते हैं जिनमें दो असंकरित कक्षक होते हैं, अर्थात् $2 p_y$ और $2 p_x$।

एक कार्बन परमाणु का एक sp संकरित कक्षक अन्य कार्बन परमाणु के sp संकरित कक्षक से अक्षीय रूप से ओवरलैप करके $\mathrm{C}-\mathrm{C}$ सिग्मा बंध बनाता है, जबकि प्रत्येक कार्बन परमाणु का अन्य संकरित कक्षक हाइड्रोजन परमाणुओं के आधे भरे s कक्षक से अक्षीय रूप से ओवरलैप कर σ बंध बनाता है। दोनों कार्बन परमाणुओं के दो असंकरित p कक्षक पार्श्व रूप से ओवरलैप कर कार्बन परमाणुओं के बीच दो π बंध बनाते हैं। इस प्रकार दो कार्बन परमाणुओं के बीच ट्रिपल बंध एक सिग्मा और दो पाई बंधों से बना होता है जैसा कि चित्र 4.16 में दिखाया गया है।

चित्र 4.16 एथाइन में सिग्मा और पाई बंधों का निर्माण

4.6.3 d कक्षकों से संबंधित तत्वों का संकरण

तीसरी अवधि में उपस्थित तत्वों में $s$ और $p$ कक्षकों के अतिरिक्त $d$ कक्षक भी होते हैं। $3d$ कक्षकों की ऊर्जा $3s$ और $3p$ कक्षकों की ऊर्जा के समतुल्य होती है। $3d$ कक्षकों की ऊर्जा $4s$ और $4p$ कक्षकों की ऊर्जा से भी तुलनीय होती है। परिणामस्वरूप, या तो $3s, 3p$ और $3d$ या $3d, 4s$ और $4p$ से संबंधित संकरण संभव है। हालांकि, चूँकि $3p$ और $4s$ कक्षकों की ऊर्जाओं में अंतर महत्वपूर्ण है, इसलिए $3p, 3d$ और $4s$ कक्षकों से संबंधित कोई संकरण संभव नहीं है।

$s, p$ और $d$ कक्षकों से संबंधित महत्वपूर्ण संकरण योजनाओं का सार नीचे दिया गया है:

(i) $\mathrm{PCl}_{5}$ का निर्माण ($\mathrm{sp}^{3}\mathrm{d}$ संकरण): फॉस्फोरस $(Z=15)$ की भूमि अवस्था और उत्तेजित अवस्था की बाह्य इलेक्ट्रॉनिक विन्यास नीचे दर्शाई गई है।

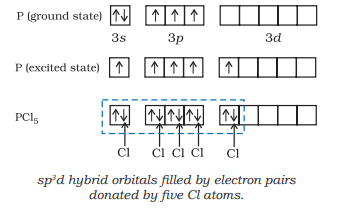
अब पाँच कक्षक (अर्थात् एक $s$, तीन $p$ और एक $d$ कक्षक) संकरण के लिए उपलब्ध हैं ताकि पाँच $s p^{3} d$ संकर कक्षकों का एक समूह प्राप्त हो सके जो त्रिसम द्विपिरैमिड के पाँच कोनों की ओर निर्देशित होते हैं जैसा कि चित्र 4.17 में दिखाया गया है।

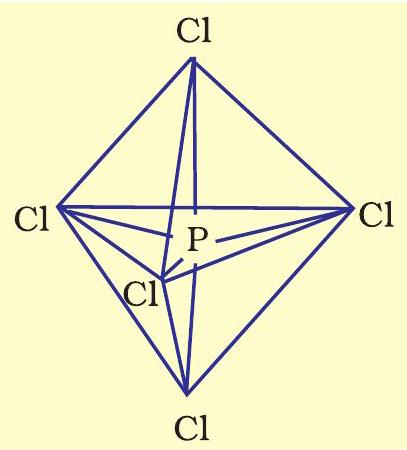
चित्र 4.17 $PCl_5$ अणु की त्रिसम द्विपिरैमिडीय ज्यामिति

यह ध्यान देना चाहिए कि त्रिसम द्विपिरैमिडीय ज्यामिति में सभी आबंध कोण समतुल्य नहीं होते हैं। $\mathrm{PCl}_5$ में फॉस्फोरस के पाँच $s p^{3} d$ कक्षक क्लोरीन परमाणुओं के एकल-आबद्ध $p$ कक्षकों से अतिव्यापन कर पाँच $\mathrm{P}-\mathrm{Cl}$ सिग्मा आबंध बनाते हैं। तीन $\mathrm{P}-\mathrm{Cl}$ आबंध एक ही तल में स्थित होते हैं और एक-दूसरे से $120^{\circ}$ का कोण बनाते हैं; इन आबंधों को भूवृत्तीय आबंध कहा जाता है। शेष दो $\mathrm{P}-\mathrm{Cl}$ आबंध—एक भूवृत्तीय तल के ऊपर और दूसरा तल के नीचे स्थित—तल से $90^{\circ}$ का कोण बनाते हैं। इन आबंधों को अक्षीय आबंध कहा जाता है। चूँकि अक्षीय आबंध युग्मों को भूवृत्तीय आबंध युग्मों से अधिक प्रतिकर्षण अंतःक्रिया झेलनी पड़ती है, इसलिए अक्षीय आबंध थोड़े लंबे और इसलिए थोड़े कमजोर पाए गए हैं; जिससे $\mathrm{PCl}_5$ अणु अधिक सक्रिय बन जाता है।

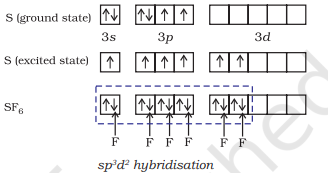
(ii) $\mathbf{S F}_6$ का निर्माण ($\mathrm{sp}^{3} d^{2}$ संकरण): $\mathrm{SF}_6$ में केंद्रीय सल्फर परमाणु की भूमिका अवस्था की बाह्य इलेक्ट्रॉनिक विन्यास $3 s^{2} 3 p^{4}$ है। उत्तेजित अवस्था में उपलब्ध छह कक्षक अर्थात् एक s, तीन $p$ और दो $d$ इलेक्ट्रॉनों से एकल-एकल भरे होते हैं। ये कक्षक छह नए $s p^{3} d^{2}$ संकर कक्षक बनाने के लिए संकरित होते हैं, जो $\mathrm{SF}_6$ में एक नियमित अष्टफलक के छह कोनों की ओर उन्मुख होते हैं। ये छह $s p^{3} d^{2}$ संकर कक्षक फ्लोरीन परमाणुओं के एकल-भरे कक्षकों से अतिव्यापन कर छह $\mathrm{S}-\mathrm{F}$ सिग्मा बंध बनाते हैं। इस प्रकार $\mathrm{SF}_6$ अणु का नियमित अष्टफलकीय ज्यामिति होती है जैसा कि चित्र 4.18 में दिखाया गया है।

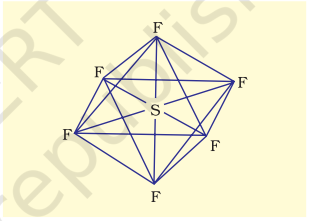
चित्र 4.18 SF6 अणु की अष्टफलकीय ज्यामिति

4.7 आण्विक कक्षक सिद्धांत

आण्विक कक्षक (MO) सिद्धांत F. हुंड और R.S. मुलिकेन ने 1932 में विकसित किया। इस सिद्धांत की प्रमुख विशेषताएँ हैं :

(i) एक अणु में इलेक्ट्रॉन विभिन्न आण्विक कक्षकों में उपस्थित होते हैं, जिस प्रकार परमाणुओं के इलेक्ट्रॉन विभिन्न परमाण्वीय कक्षकों में उपस्थित होते हैं।

(ii) तुलनात्मक ऊर्जाओं और उचित सममिति वाले परमाण्वीय कक्षक संयुक्त होकर आण्विक कक्षक बनाते हैं।

(iii) जबकि एक परमाण्वीय कक्षक में इलेक्ट्रॉन एक नाभिक के प्रभाव में होता है, एक आण्विक कक्षक में वह दो या अधिक नाभिकों के प्रभाव में होता है, जो अणु में परमाणुओं की संख्या पर निर्भर करता है। इस प्रकार, एक परमाण्वीय कक्षक एककेन्द्रकीय होता है जबकि एक आण्विक कक्षक बहुकेन्द्रकीय होता है।

(iv) बनने वाले आण्विक कक्षकों की संख्या संयुक्त होने वाले परमाण्वीय कक्षकों की संख्या के बराबर होती है। जब दो परमाण्वीय कक्षक संयुक्त होते हैं, तो दो आण्विक कक्षक बनते हैं। एक को आबंधन आण्विक कक्षक कहा जाता है जबकि दूसरे को प्रतिआबंधन आण्विक कक्षक कहा जाता है।

(v) आबंधन आण्विक कक्षक की ऊर्जा कम होती है और इसलिए संगत प्रतिआबंधन आण्विक कक्षक की तुलना में इसकी अधिक स्थिरता होती है।

(vi) जिस प्रकार एक परमाणु में नाभिक के चारों ओर इलेक्ट्रॉन प्रायिकता वितरण एक परमाण्वीय कक्षक द्वारा दिया जाता है, उसी प्रकार एक अणु में नाभिकों के समूह के चारों ओर इलेक्ट्रॉन प्रायिकता वितरण एक आण्विक कक्षक द्वारा दिया जाता है।

(vii) आण्विक कक्षक, परमाण्वीय कक्षकों की भांति, आउफ़बाउ सिद्धांत के अनुसार, पाउली के निषेध सिद्धांत तथा हुंड नियम का पालन करते हुए भरे जाते हैं।

4.7.1 आण्विक कक्षकों का निर्माण परमाण्वीय कक्षकों की रेखीय संयोजन (LCAO)

तरंग यांत्रिकी के अनुसार, परमाण्वीय कक्षकों को तरंग फलनों ($\psi$’s) द्वारा व्यक्त किया जा सकता है जो इलेक्ट्रॉन तरंगों के आयाम को दर्शाते हैं। ये श्रोडिंगर तरंग समीकरण के हल से प्राप्त होते हैं। हालांकि, चूंकि इसे एक से अधिक इलेक्ट्रॉन वाले किसी भी तंत्र के लिए हल नहीं किया जा सकता, अणुकक्षक जो अणुओं के लिए एक-इलेक्ट्रॉन तरंग फलन हैं, श्रोडिंगर तरंग समीकरण के हल से सीधे प्राप्त करना कठिन होता है। इस समस्या को दूर करने के लिए, एक सन्निकट विधि जिसे परमाण्वीय कक्षकों का रैखिक संयोजन (LCAO) कहा जाता है, अपनाई गई है।

आइए इस विधि को समान नाभिकीय द्विपरमाणुक हाइड्रोजन अणु पर लागू करें। हाइड्रोजन अणु पर विचार करें जिसमें दो परमाणु A और B हैं। प्रत्येक हाइड्रोजन परमाणु आधार अवस्था में $1 \mathrm{~s}$ कक्षक में एक इलेक्ट्रॉन रखता है। इन परमाणुओं के परमाण्वीय कक्षकों को तरंग फलनों $\psi_{\mathrm{A}}$ और $\psi_{\mathrm{B}}$ द्वारा दर्शाया जा सकता है। गणितीय रूप से, अणुकक्षकों का निर्माण परमाण्वीय कक्षकों के रैखिक संयोजन द्वारा वर्णित किया जा सकता है जो व्यक्तिगत परमाण्वीय कक्षकों के तरंग फलनों के योग और व्यवकलन द्वारा हो सकता है जैसा कि नीचे दिखाया गया है:

$$ \psi_{\mathrm{MO}}=\psi_{\mathrm{A}} \pm \psi_{\mathrm{B}} $$

इसलिए, दो अणुकक्षक $\sigma$ और $\sigma^{*}$ इस प्रकार बनते हैं:

$$ \begin{aligned} & \sigma=\psi_{\mathrm{A}}+\psi_{\mathrm{B}} \ & \sigma^{*}=\psi_{\mathrm{A}}-\psi_{\mathrm{B}} \end{aligned} $$

परमाण्वीय कक्षकों के योग से बना आण्विक कक्षक $\sigma$ आबंधन आण्विक कक्षक कहलाता है, जबकि परमाण्वीय कक्षकों के घटाव से बना आण्विक कक्षक $\sigma^{*}$ प्रतिआबंधन आण्विक कक्षक कहलाता है जैसा कि चित्र 4.19 में दिखाया गया है।

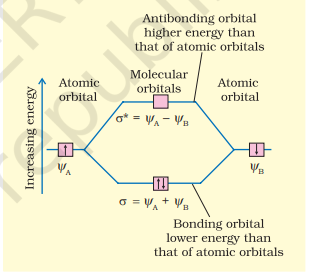
चित्र 4.19 दो परमाणुओं A और B पर केंद्रित परमाण्वीय कक्षकों ψA और ψB के रैखिक संयोजन द्वारा आबंधन (σ) और प्रतिआबंधन (σ*) आण्विक कक्षकों का निर्माण।

गुणात्मक रूप से, आण्विक कक्षकों का निर्माण संयोजी परमाणुओं की इलेक्ट्रॉन तरंगों की रचनात्मक या विनाशकारी व्यतिकरण के संदर्भ में समझा जा सकता है। संयोजी आण्विक कक्षक के निर्माण में, संयोजी परमाणुओं की दो इलेक्ट्रॉन तरंगें रचनात्मक व्यतिकरण के कारण एक-दूसरे को बल प्रदान करती हैं, जबकि प्रतिसंयोजी आण्विक कक्षक के निर्माण में, इलेक्ट्रॉन तरंगें विनाशकारी व्यतिकरण के कारण एक-दूसरे को रद्द कर देती हैं। परिणामस्वरूप, संयोजी आण्विक कक्षक में इलेक्ट्रॉन घनत्व संयोजी परमाणुओं के नाभिकों के बीच स्थित होता है, जिससे नाभिकों के बीच प्रतिकर्षण बहुत कम होता है, जबकि प्रतिसंयोजी आण्विक कक्षक में अधिकांश इलेक्ट्रॉन घनत्व नाभिकों के बीच के स्थान से दूर स्थित होता है। वास्तव में, नाभिकों के बीच एक नोडल समतल (जिस पर इलेक्ट्रॉन घनत्व शून्य होता है) होता है और इसलिए नाभिकों के बीच प्रतिकर्षण अधिक होता है। संयोजी आण्विक कक्षक में रखे गए इलेक्ट्रॉन नाभिकों को एक साथ रखने और अणु को स्थिर करने की प्रवृत्ति रखते हैं। इसलिए, संयोजी आण्विक कक्षक की ऊर्जा हमेशा उन परमाण्विक कक्षकों की तुलना में कम होती है जिनसे इसका निर्माण हुआ है। इसके विपरीत, प्रतिसंयोजी आण्विक कक्षक में रखे गए इलेक्ट्रॉन अणु को अस्थिर करते हैं। ऐसा इसलिए है क्योंकि इस कक्षक में इलेक्ट्रॉनों का आपसी प्रतिकर्षण इलेक्ट्रॉनों और नाभिकों के बीच के आकर्षण से अधिक होता है, जिससे ऊर्जा में शुद्ध वृद्धि होती है।

यह ध्यान दिया जा सकता है कि प्रतिबंधन कक्षक की ऊर्जा मूल परमाणवीय कक्षकों की ऊर्जा से ऊपर बढ़ा दी गई है जिन्होंने संयोजन किया है और बंधन कक्षक की ऊर्जा मूल कक्षकों से नीचे कर दी गई है। दो आण्विक कक्षकों की कुल ऊर्जा, हालांकि, दो मूल परमाणवीय कक्षकों की ऊर्जा के समान ही रहती है।

4.7.2 परमाणवीय कक्षकों के संयोजन की शर्तें

परमाणवीय कक्षकों का रैखिक संयोजन आण्विक कक्षक बनाने के लिए तभी होता है जब निम्नलिखित शर्तें पूरी हों:

1. संयोजित होने वाले परमाणवीय कक्षकों की ऊर्जा समान या लगभग समान होनी चाहिए। इसका अर्थ है कि $1 \mathrm{~s}$ कक्षक दूसरे $1 s$ कक्षक के साथ संयोजन कर सकता है लेकिन $2 s$ कक्षक के साथ नहीं क्योंकि $2 s$ कक्षक की ऊर्जा $1 \mathrm{~s}$ कक्षक की तुलना में काफी अधिक है। यह सच नहीं है यदि परमाणु बहुत भिन्न हों।

2. संयोजित होने वाले परमाणवीय कक्षकों की आण्विक अक्ष के परितः समान सममिति होनी चाहिए। परंपरा से $z$-अक्ष को आण्विक अक्ष माना जाता है। यह ध्यान देना महत्वपूर्ण है कि समान या लगभग समान ऊर्जा वाले परमाणवीय कक्षक संयोजन नहीं करेंगे यदि उनकी सममिति समान न हो। उदाहरण के लिए, एक परमाणु का $2 p_{z}$ कक्षक दूसरे परमाणु के $2 p_{z}$ कक्षक के साथ संयोजन कर सकता है लेकिन $2 p_{x}$ या $2 p_{y}$ कक्षकों के साथ नहीं क्योंकि उनकी सममितियां भिन्न हैं।

3. संयुक्त परमाण्वीय कक्षकों का अधिकतम सीमा तक अतिव्यापन होना चाहिए। अतिव्यापन की सीमा जितनी अधिक होगी, अणुक कक्षक के नाभिकों के बीच इलेक्ट्रॉन-घनत्व उतना ही अधिक होगा।

4.7.3 अणुक कक्षकों के प्रकार

द्विपरमाण्विक अणुओं के अणुक कक्षकों को $\sigma$ (सिग्मा), $\pi$ (पाई), $\delta$ (डेल्टा) आदि के रूप में नामित किया जाता है। इस नामकरण में, सिग्मा $(\sigma)$ अणुक कक्षक बंध-अक्ष के परितः सममित होते हैं जबकि पाई $(\pi)$ अणुक कक्षक सममित नहीं होते हैं। उदाहरण के लिए, दो नाभिकों पर केंद्रित $1 \mathrm{~s}$ कक्षकों की रैखिक संयोजन दो ऐसे अणुक कक्षक उत्पन्न करती है जो बंध-अक्ष के परितः सममित होते हैं। ऐसे अणुक कक्षक $\sigma$ प्रकार के होते हैं और इन्हें $\sigma 1 \mathrm{~s}$ और $\sigma^* 1 \mathrm{~s}$ के रूप में नामित किया जाता है [चित्र 4.20(a), पृष्ठ 124]। यदि अंतरनाभिकीय अक्ष को $\mathrm{z}$-दिशा में लिया जाए, तो यह देखा जा सकता है कि दो परमाणुओं के $2 p_z$-कक्षकों की रैखिक संयोजन भी दो सिग्मा अणुक कक्षक उत्पन्न करती है जिन्हें $\boldsymbol{\sigma} \boldsymbol{p}_z$ और $\sigma^{\boldsymbol{*}} \boldsymbol{2}_z$ के रूप में नामित किया जाता है। [चित्र 4.20(b)]

$2 p_{\mathrm{x}}$ और $2 p$ कक्षकों से प्राप्त आण्विक कक्षक बंध अक्ष के परितः सममित नहीं होते हैं, क्योंकि आण्विक तल के ऊपर धनात्मक लोब और नीचे ऋणात्मक लोब उपस्थित होते हैं। ऐसे आण्विक कक्षकों को $\pi$ और $\pi^{*}$ के रूप में चिह्नित किया जाता है [चित्र 4.20(c)]। एक $\pi$ बंधन आण्विक कक्षक में नाभिकीय अक्ष के ऊपर और नीचे इलेक्ट्रॉन घनता अधिक होती है। $\pi^{\star}$ प्रतिबंधन आण्विक कक्षक में नाभिकों के बीच एक नोड होता है।

4.7.4 आण्विक कक्षकों के लिए ऊर्जा स्तर आरेख

हमने देखा है कि दो परमाणुओं पर स्थित $1 \mathrm{~s}$ परमाण्वीय कक्षक दो आण्विक कक्षक बनाते हैं, जिन्हें $\sigma 1 \mathrm{~s}$ और $\sigma^{*} 1 \mathrm{~s}$ के रूप में नामित किया गया है। इसी प्रकार, $2 \mathrm{~s}$ और $2 p$ परमाण्वीय कक्षक (दो परमाणुओं पर कुल आठ परमाण्वीय कक्षक) निम्नलिखित आठ आण्विक कक्षक उत्पन्न करते हैं:

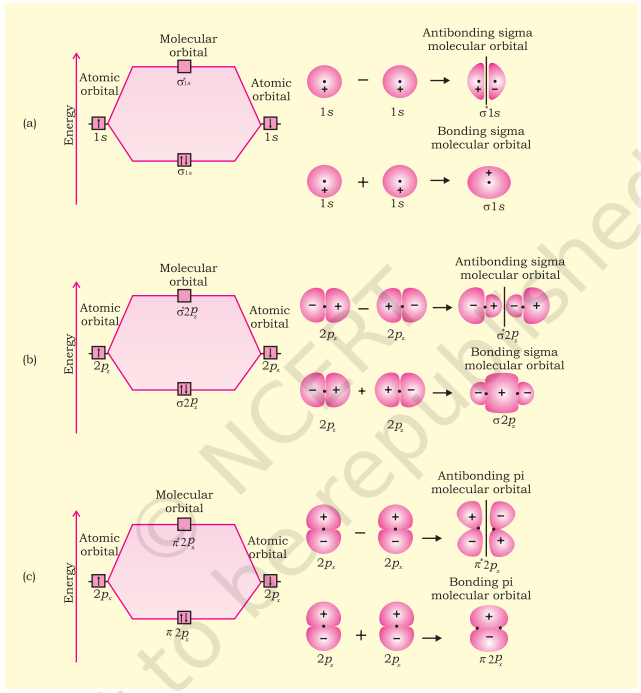
चित्र 4.20 (a) 1s परमाण्वीय कक्षकों; (b) $2p_z$ परमाण्वीय कक्षकों और (c) $2p_x$ परमाण्वीय कक्षकों के संयोजन से बने बंधन और प्रतिबंधन आण्विक कक्षकों के समोच्च और ऊर्जाएँ।

$\begin{array}{llllll} \text{प्रतिबंधन } & \mathrm{MOs} & \sigma^* 2 s & \sigma^* 2 p_z & \pi^* 2 p_x & \pi^* 2 p_y \\ \text { बंधन } & \mathrm{MOs} & \sigma 2 \mathrm{~s} & \sigma 2 p_{z} & \pi 2 p_{x} & \pi 2 p_{y}\end{array}$

इन आण्विक कक्षकों की ऊर्जा स्तरों का निर्धारण आवर्त सारणी के द्वितीय पंक्ति के तुल्य परमाणु द्वि-परमाणु अणुओं के स्पेक्ट्रोस्कोपिक आँकड़ों से प्रयोगात्मक रूप से किया गया है। $\mathrm{O}_2$ और $\mathrm{F}_2$ के लिए विभिन्न आण्विक कक्षकों की ऊर्जाओं का बढ़ता हुआ क्रम नीचे दिया गया है:

$\sigma 1 s<\sigma^* 1 s<\sigma 2 s<\sigma^* 2 s<\sigma 2 p_z < \left(\pi 2 p_x = \pi 2 p_y\right) $

$<\left(\pi^* 2 p_x=\pi^* 2 p_y\right) < \sigma^* 2 p_z$

हालाँकि, आण्विक कक्षकों की ऊर्जा स्तरों की यह अनुक्रम शेष अणुओं $\mathrm{Li}_2, \mathrm{Be}_2, \mathrm{~B}_2, \mathrm{C}_2, \mathrm{~N}_2$ के लिए सही नहीं है। उदाहरण के लिए, यह प्रयोगात्मक रूप से देखा गया है कि $\mathrm{B}_2, \mathrm{C}_2, \mathrm{~N}_2$ आदि अणुओं के लिए विभिन्न आण्विक कक्षकों की ऊर्जाओं का बढ़ता हुआ क्रम

$\sigma 1 s<\sigma^* 1 s<\sigma 2 s<\sigma^* 2 s<\left(\pi 2 p_x=\pi 2 p_y\right)$

$<\sigma 2 p_z<\left(\pi^* 2 p_x=\pi^* 2 p_y\right)<\sigma^* 2 p_z$

इस क्रम का महत्वपूर्ण लक्षण यह है कि $\boldsymbol{\sigma 2} \boldsymbol{p}_z$ आण्विक कक्षक की ऊर्जा, $\pi 2 p_x$ और $\pi 2 p_y$ आण्विक कक्षकों की ऊर्जा से अधिक होती है।

4.7.5 इलेक्ट्रॉनिक विन्यास और आण्विक व्यवहार

विभिन्न आण्विक कक्षकों में इलेक्ट्रॉनों का वितरण अणु का इलेक्ट्रॉनिक विन्यास कहलाता है। अणु के इलेक्ट्रॉनिक विन्यास से, नीचे चर्चा किए अनुसार, अणु के बारे में महत्वपूर्ण जानकारी प्राप्त करना संभव है।

अणुओं की स्थिरता: यदि $\mathrm{N}_b$ बंधन कक्षकों में उपस्थित इलेक्ट्रॉनों की संख्या है और $\mathrm{N}_a$ प्रतिबंधन कक्षकों में उपस्थित इलेक्ट्रॉनों की संख्या है, तो

(i) अणु स्थिर है यदि $\mathrm{N}_b$, $\mathrm{N}_a$ से अधिक है, और

(ii) अणु अस्थिर है यदि $\mathrm{N}_b$, $\mathrm{N}_a$ से कम है।

(i) में अधिक बंधन कक्षक भरे होते हैं इसलिए बंधन प्रभाव अधिक मजबूत होता है और एक स्थिर अणु बनता है। (ii) में प्रतिबंधन प्रभाव अधिक मजबूत होता है और इसलिए अणु अस्थिर होता है।

बंध क्रम

बंध क्रम (b.o.) को बंधन और प्रतिबंधन कक्षकों में उपस्थित इलेक्ट्रॉनों की संख्या के बीच के अंतर का आधा परिभाषित किया गया है, अर्थात्,

बंध क्रम (b.o.) $=1 / 2\left(\mathrm{~N}_b-\mathrm{N}_a\right)$

उपरोक्त चर्चा की गई नियमों को बंध क्रम के संदर्भ में इस प्रकार पुनः कहा जा सकता है: एक धनात्मक बंध क्रम (अर्थात्, $\mathrm{N}_b>\mathrm{N}_a$) एक स्थिर अणु का अर्थ है जबकि एक ऋणात्मक (अर्थात्, $\mathrm{N}_b < \mathrm{N}_a$) या शून्य (अर्थात्, $\mathrm{N}_b=\mathrm{N}_a$) बंध क्रम एक अस्थिर अणु का अर्थ है।

बंध की प्रकृति

एकीकृत बंध क्रम मान 1, 2 या 3 क्रमशः एकल, द्विगुणित या त्रिगुणित बंधों के अनुरूप होते हैं जैसा कि शास्त्रीय अवधारणा में अध्ययन किया गया है।

बंध-लंबाई

किसी अणु में दो परमाणुओं के बीच बंध क्रम को बंध लंबाई का एक सन्निकट माप माना जा सकता है। बंध क्रम बढ़ने पर बंध लंबाई घटती है।

चुंबकीय प्रकृति

यदि किसी अणु के सभी आण्विक कक्षाएँ द्विआबद्ध हों, तो पदार्थ प्रतिचुंबकीय होता है (चुंबकीय क्षेत्र से प्रतिकर्षित होता है)। यदि एक या अधिक आण्विक कक्षाएँ एकल आबद्ध हों तो वह अनुचुंबकीय होता है (चुंबकीय क्षेत्र से आकर्षित होता है), उदाहरण के लिए, $\mathrm{O}_{2}$ अणु।

4.8 कुछ समान केंद्र द्विपरमाण्विक अणुओं में बंधन

इस खंड में हम कुछ समान केंद्र द्विपरमाण्विक अणुओं में बंधन की चर्चा करेंगे।

1. हाइड्रोजन अणु $\left(\boldsymbol{H}_{2}\right)$ : यह दो हाइड्रोजन परमाणुओं के संयोजन से बनता है। प्रत्येक हाइड्रोजन परमाणु में 1s कक्षक में एक इलेक्ट्रॉन होता है। इसलिए, कुल मिलाकर हाइड्रोजन अणु में दो इलेक्ट्रॉन होते हैं जो $\sigma 1 \mathrm{~s}$ आण्विक कक्षक में उपस्थित होते हैं। इसलिए हाइड्रोजन अणु का इलेक्ट्रॉनिक विन्यास है

$$ \mathrm{H}_{2}:(\sigma 1 s)^{2} $$

$\mathrm{H}_{2}$ अणु का बंध क्रम नीचे दिए गए अनुसार गणना किया जा सकता है:

$$ \text { बंध क्रम }=\frac{\mathrm{N}_b-\mathrm{N}_a}{2}=\frac{2-0}{2}=1 $$

इसका अर्थ है कि दो हाइड्रोजन परमाणु एकल सहसंयोजक बंध द्वारा एक साथ बंधित हैं। हाइड्रोजन अणु की बंध विघटन ऊर्जा $438 \mathrm{~kJ} \mathrm{~mol}^{-1}$ पाई गई है और बंध लंबाई $74 \mathrm{pm}$ के बराबर है। चूँकि हाइड्रोजन अणु में कोई अयुग्मित इलेक्ट्रॉन उपस्थित नहीं है, इसलिए यह प्रतिचुंबकीय है।

2. हीलियम अणु $\left(\mathbf{H e}_2\right)$ : हीलियम परमाणु का इलेक्ट्रॉनिक विन्यास $1 s^2$ है। प्रत्येक हीलियम परमाणु में 2 इलेक्ट्रॉन होते हैं, इसलिए $\mathrm{He}_2$ अणु में 4 इलेक्ट्रॉन होंगे। ये इलेक्ट्रॉन $\sigma 1 s$ और $\sigma^{*} 1 s$ आण्विक कक्षकों में समायोजित होंगे जिससे इलेक्ट्रॉनिक विन्यास होगा:

$\mathrm{He}_{2}:(\sigma 1 s)^{2}\left(\sigma^{*} 1 s\right)^{2}$

$\mathrm{He}_{2}$ की बंध कोटि $1 / 2(2-2)=0$ है

$\mathrm{He}_{2}$ अणु इसलिए अस्थिर है और अस्तित्व में नहीं है।

इसी प्रकार, यह दिखाया जा सकता है कि $\mathrm{Be}_2$ अणु $(\sigma 1 s)^2\left(\sigma^* 1 s\right)^2(\sigma 2 s)^2\left(\sigma^* 2 s\right)^2$ भी अस्तित्व में नहीं है।

3. लिथियम अणु $\left(\mathbf{L i}_2\right)$ : लिथियम का इलेक्ट्रॉनिक विन्यास $1 s^2, 2 s^1$ है। $\mathrm{Li}_2$ में छह इलेक्ट्रॉन होते हैं। $\mathrm{Li}_2$ अणु का इलेक्ट्रॉनिक विन्यास, इसलिए, है

$$ \operatorname{Li}_{2}:(\sigma 1 s)^{2}\left(\sigma^{*} 1 s\right)^{2}(\sigma 2 s)^{2} $$

उपरोक्त विन्यास को $\mathrm{KK}(\sigma 2 \mathrm{~s})^{2}$ के रूप में भी लिखा जाता है, जहाँ $\mathrm{KK}$ बंद $K$ शैल संरचना $(\sigma 1 s)^{2}\left(\sigma^{*} 1 s\right)^{2}$ को दर्शाता है।

$\mathrm{Li}_2$ अणु के इलेक्ट्रॉनिक विन्यास से यह स्पष्ट है कि चार इलेक्ट्रॉन बंधन आण्विक कक्षकों में उपस्थित हैं और दो इलेक्ट्रॉन प्रतिबंधन आण्विक कक्षकों में उपस्थित हैं। इसका बंध क्रम, इसलिए, $1 / 2$ (42) $=1$ है। इसका अर्थ है कि $\mathrm{Li}_2$ अणु स्थिर है और चूँकि इसमें कोई अयुग्मित इलेक्ट्रॉन नहीं है, यह प्रतिचुंबकीय होना चाहिए। वास्तव में प्रतिचुंबकीय $\mathrm{Li}_2$ अणुओं का अस्तित्व वाष्प चरण में जाना जाता है।

4. कार्बन अणु $\left(\boldsymbol{C}_2\right)$ : कार्बन का इलेक्ट्रॉनिक विन्यास $1 s^{2} 2 s^{2} 2 p^{2}$ है। $\mathrm{C}_2$ में बारह इलेक्ट्रॉन हैं। $\mathrm{C}_2$ अणु का इलेक्ट्रॉनिक विन्यास, इसलिए, है

$\mathrm{C}_2:(\sigma 1 \mathrm{~s})^{2}\left(\sigma^{*} 1 \mathrm{~s}\right)^{2}(\sigma * 2 \mathrm{~s})^{2}\left(\pi 2 \mathrm{p}_x^{2}=\pi 2 \mathrm{p}_y^{2}\right)$

या $K K(\sigma 2 s)^{2}(\sigma * 2 s)^{2}\left(\pi 2 \mathrm{p}_x^{2}=\pi 2 \mathrm{p}_y^{2}\right)$

$\mathrm{C}_2$ का बंध क्रम $1 / 2(8-4)=2$ है और $\mathrm{C}_2$ प्रतिचुंबकीय होना चाहिए। प्रतिचुंबकीय $\mathrm{C}_2$ अणुओं को वास्तव में वाष्प चरण में देखा गया है। यह ध्यान देना महत्वपूर्ण है कि $\mathrm{C}_2$ में द्विबंध दोनों पाई बंधों से बना होता है क्योंकि दो पाई आण्विक कक्षकों में चार इलेक्ट्रॉन मौजूद होते हैं। अधिकांश अन्य अणुओं में एक द्विबंध एक सिग्मा बंध और एक पाई बंध से बना होता है। इसी प्रकार $\mathrm{N}_2$ अणु में बंधन पर चर्चा की जा सकती है।

5. ऑक्सीजन अणु $\left(\mathrm{O}_2\right)$ : ऑक्सीजन परमाणु का इलेक्ट्रॉनिक विन्यास $1 s^{2} 2 s^{2} 2 p^{4}$ है। प्रत्येक ऑक्सीजन परमाणु में 8 इलेक्ट्रॉन होते हैं, इसलिए $\mathrm{O}_2$ अणु में 16 इलेक्ट्रॉन होते हैं। $\mathrm{O}_2$ अणु का इलेक्ट्रॉनिक विन्यास, इसलिए, है

$\mathrm{O}_{2}:(\sigma 1 s)^{2}\left(\sigma^{*} 1 s\right)^{2}(\sigma 2 s)^{2}(\sigma * 2 s)^{2}\left(\sigma 2 \mathrm{p}_z\right)^{2}$

$\left(\pi 2 p_x{ }^{2} \equiv \pi 2 p_y{ }^{2}\right)\left(\pi^{*} 2 p^{1}{ }_x \equiv \pi * 2 p_y{ }^{1}\right)$

या $\mathrm{O}^{2}:\left[\begin{array}{c}\mathrm{KK}(\sigma 2 \mathrm{~s})^{2}\left(\sigma 2 p_S\right)^{2}\left(\sigma 2 p_z\right)^{2} \\ \left(\pi 2 p_x^{2} \equiv \pi 2 p_y^{2}\right),\left(\pi * 2 \mathrm{p}_x^{1} \equiv \pi * 2_y^{1}\right)\end{array}\right]$

$\mathrm{O}_{2}$ अणु की इलेक्ट्रॉनिक विन्यास से यह स्पष्ट है कि दस इलेक्ट्रॉन बंधन आण्विक कक्षकों में उपस्थित हैं और छह इलेक्ट्रॉन प्रतिबंधन आण्विक कक्षकों में उपस्थित हैं। इसका बंधन कोटि, इसलिए है

बंधन कोटि $=\frac{1}{2}\left[N_{b}-N_{a}\right]=\frac{1}{2}[10-6]=2$

इसलिए ऑक्सीजन अणु में, परमाणु एक द्विबंध द्वारा आयोजित होते हैं। इसके अतिरिक्त, यह उल्लेखनीय है कि इसमें $\pi^* 2 p_x$ और $\pi^* 2 p_y$ आण्विक कक्षकों में दो अयुग्मित इलेक्ट्रॉन होते हैं, इसलिए, $\mathrm{O}_2$ अणु अनुचुंबकीय होना चाहिए, एक भविष्यवाणी जो प्रयोगात्मक प्रेक्षण से मेल खाती है। इस प्रकार, सिद्धांत ऑक्सीजन की अनुचुंबकीय प्रकृति को सफलतापूर्वक समझाता है।

इसी प्रकार, आवर्त सारणी की दूसरी पंक्ति के अन्य समपरमाणुक द्विपरमाण्विक अणुओं की इलेक्ट्रॉनिक विन्यास लिखी जा सकती हैं। चित्र 4.21 में $\mathrm{B}_2$ से $\mathrm{Ne}_2$ तक के लिए आण्विक कक्षक व्यस्तता और आण्विक गुण दिए गए हैं। आण्विक कक्षकों की अनुक्रम और उनकी इलेक्ट्रॉन जनसंख्या दिखाई गई है। बंधन ऊर्जा, बंधन लंबाई, बंधन कोटि, चुंबकीय गुण और संयोजकता इलेक्ट्रॉन विन्यास कक्षक आरेखों के नीचे दिखाई देते हैं।

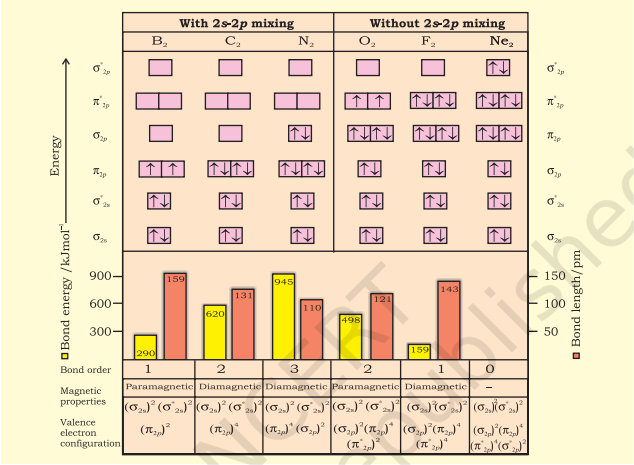
चित्र 4.21 $B_2$ से $Ne_2$ तक के लिए आण्विक कक्षक व्यस्तता और आण्विक गुण।

4.9 हाइड्रोजन बंधन

नाइट्रोजन, ऑक्सीजन और फ्लोरीन अत्यधिक विद्युत-ऋणात्मक तत्व हैं। जब ये किसी हाइड्रोजन परमाणु से सहसंयोजक बंध बनाने के लिए जुड़ते हैं, तो सहसंयोजक बंध के इलेक्ट्रॉन अधिक विद्युत-ऋणात्मक परमाणु की ओर सरक जाते हैं। यह आंशिक रूप से धनावेशित हाइड्रोजन परमाणु दूसरे अधिक विद्युत-ऋणात्मक परमाणु से बंध बनाता है। इस बंध को हाइड्रोजन बंध कहा जाता है और यह सहसंयोजक बंध से कमजोर होता है। उदाहरण के लिए, HF अणु में हाइड्रोजन बंध एक अणु के हाइड्रोजन परमाणु और दूसरे अणु के फ्लोरीन परमाणु के बीच होता है जैसा नीचे दिखाया गया है:

$\text{ - - - }\mathrm{H}^{\delta+}-\mathrm{F}^{\delta-}\text{ - - - }\mathrm{H}^{\delta+}-\mathrm{F}^{\delta-}\text{ - - - }\mathrm{H}^{\delta+}-\mathrm{F}^{\delta-}$

यहाँ हाइड्रोजन बंध दो परमाणुओं के बीच सेतु का कार्य करता है जो एक परमाणु को सहसंयोजक बंध से और दूसरे को हाइड्रोजन बंध से पकड़े रखता है।
हाइड्रोजन बंध को बिंदीदार रेखा ($\text{ - - - }$) से दर्शाया जाता है जबकि ठोस रेखा सहसंयोजक बंध को दर्शाती है। इस प्रकार, हाइड्रोजन बंध को आकर्षक बल के रूप में परिभाषित किया जा सकता है जो एक अणु के हाइड्रोजन परमाणु को दूसरे अणु के विद्युत-ऋणात्मक परमाणु ($\mathrm{F}, \mathrm{O}$ या $\mathrm{N}$) से बांधता है।

4.9.1 हाइड्रोजन बंध बनने का कारण

जब हाइड्रोजन एक अत्यधिक विद्युत्-ऋणात्मक तत्व ‘X’ से बंधित होता है, तो दोनों परमाणुओं के बीच साझा किया गया इलेक्ट्रॉन-युग्म हाइड्रोजन परमाणु से दूर चला जाता है। परिणामस्वरूप हाइड्रोजन परमाणु दूसरे परमाणु ‘X’ के सापेक्ष अत्यधिक विद्युत्-धनात्मक हो जाता है। चूँकि इलेक्ट्रॉनों का विस्थापन X की ओर होता है, हाइड्रोजन आंशिक धनात्मक आवेश (δ⁺) प्राप्त कर लेता है जबकि ‘X’ आंशिक ऋणात्मक आवेश (δ⁻) प्राप्त कर लेता है। इससे एक ध्रुवीय अणु बनता है जिसमें स्थिरवैद्युत आकर्षण बल होता है, जिसे इस प्रकार दर्शाया जा सकता है:

H^{δ+}-X^{δ-} - - - H^{δ+}-X^{δ-} - - - H^{δ+}-X^{δ-}

H-बंधन की तीव्रता यौगिक की भौतिक अवस्था पर निर्भर करती है। यह ठोस अवस्था में अधिकतम और गैसीय अवस्था में न्यूनतम होती है। इस प्रकार हाइड्रोजन बंध यौगिकों की संरचना और गुणधर्मों पर प्रबल प्रभाव डालते हैं।

4.9.2 H-बंधों के प्रकार

H-बंध दो प्रकार के होते हैं

(i) अंतराअण्विक हाइड्रोजन बंध

(ii) अंतःअण्विक हाइड्रोजन बंध

(1) अंतराअण्विक हाइड्रोजन बंध: यह एक ही या भिन्न यौगिकों के दो भिन्न अणुओं के बीच बनता है। उदाहरण के लिए, HF अणु, एल्कोहल या जल अणुओं आदि में H-बंध।

(2) अंतःअणुक हाइड्रोजन बंध : यह तब बनता है जब हाइड्रोजन परमाणु उच्च विद्युत्-ऋणात्मक $(\mathrm{F}, \mathrm{O}, \mathrm{N})$ परमाणुओं के बीच में होता है जो एक ही अणु में मौजूद होते हैं। उदाहरण के लिए, o-नाइट्रोफ़ेनॉल में हाइड्रोजन दो ऑक्सीजन परमाणुओं के बीच में होता है।

चित्र 4.22 अंतःअणुक हाइड्रोजन

सारांश

कोसेल की विद्युत्-धनात्मक और विद्युत्-ऋणात्मक आयनों के निर्माण की प्रक्रिया के प्रति पहली अंतर्दृष्टि थी कि यह प्रक्रिया संबंधित आयनों द्वारा निष्क्रिय गैस विन्यास प्राप्त करने से संबंधित है। आयनों के बीच स्थिरता का कारण आयनों के बीच स्थिर वैद्युत आकर्षण है। यह विद्युत्-संयोजन की अवधारणा देता है।

सहसंयोजक बंधन का पहला वर्णन लुइस ने परमाणुओं के बीच इलेक्ट्रॉन युगलों के साझाकरण के रूप में प्रदान किया और उन्होंने इस प्रक्रिया को प्रतिक्रियाशील परमाणुओं द्वारा इलेक्ट्रॉनों के साझाकरण के परिणामस्वरूप निष्क्रिय गैस विन्यास प्राप्त करने से संबद्ध किया। लुइस बिंदु प्रतीक एक दिए गए तत्व के परमाणुओं की संयोजकता इलेक्ट्रॉनों की संख्या दिखाते हैं और लुइस बिंदु संरचनाएं अणुओं में बंधन की चित्रात्मक प्रस्तुतियां दिखाती हैं।

एक आयनिक यौगिक को धनात्मक और ऋणात्मक आयनों की एक त्रि-आयामी संगठन के रूप में चित्रित किया जाता है, जो क्रिस्टल जालक (crystal lattice) नामक क्रमबद्ध व्यवस्था में होते हैं। एक क्रिस्टलीय ठोस में धनात्मक और ऋणात्मक आयनों के बीच आवेश संतुलन होता है। क्रिस्टल जालक, जालक निर्माण की एन्थैल्पी द्वारा स्थिरीकृत होता है।

जबकि एक एकल सहसंयोजक बंधन, दो परमाणुओं के बीच एक इलेक्ट्रॉन युग्म के साझाकरण से बनता है, एकाधिक बंधन दो या तीन इलेक्ट्रॉन युग्मों के साझाकरण से उत्पन्न होते हैं। कुछ बंधित परमाणुओं के पास इलेक्ट्रॉनों के अतिरिक्त युग्म होते हैं जो बंधन में संलग्न नहीं होते। इन्हें इलेक्ट्रॉनों के एकाकी-युग्म (lone-pairs) कहा जाता है। एक लुइस बिंदु संरचना (Lewis dot structure) अणु में प्रत्येक परमाणु के चारों ओर बंधित युग्मों और एकाकी युग्मों की व्यवस्था दिखाती है। रासायनिक बंधनों से संबद्ध महत्वपूर्ण पैरामीटर, जैसे: बंधन लंबाई, बंधन कोण, बंधन एन्थैल्पी, बंधन क्रम और बंधन ध्रुवता, यौगिकों के गुणों पर महत्वपूर्ण प्रभाव डालते हैं।

कई अणु और बहुपरमाणु आयन एकल लुइस संरचना द्वारा सटीक रूप से वर्णित नहीं किए जा सकते और एक ही कंकाल संरचना पर आधारित कई वर्णन (प्रतिनिधित्व) लिखे जाते हैं और इन्हें एक साथ लेकर अणु या आयन का प्रतिनिधित्व किया जाता है। यह एक अत्यंत महत्वपूर्ण और अत्यंत उपयोगी अवधारणा है जिसे अनुनाद (resonance) कहा जाता है। योगदान करने वाली संरचनाएं या मानक रूप एक साथ मिलकर अनुनादी संकर (resonance hybrid) का निर्माण करती हैं जो अणु या आयन का प्रतिनिधित्व करता है।

VSEPR मॉडल, जिसका उपयोग अणुओं की ज्यामितीय आकृतियों की भविष्यवाणी के लिए किया जाता है, इस धारणा पर आधारित है कि इलेक्ट्रॉन युगल एक-दूसरे को प्रतिकर्षित करते हैं और इसलिए वे यथासंभव दूर रहने का प्रयास करते हैं। इस मॉडल के अनुसार, आण्विक ज्यामिति का निर्धारण एकाकी युगलों और एकाकी युगलों; एकाकी युगलों और आबंधन युगलों तथा आबंधन युगलों और आबंधन युगलों के बीच प्रतिकर्षण द्वारा होता है। इन प्रतिकर्षणों का क्रम इस प्रकार है : lp-lp $>1 \mathrm{p}-\mathrm{bp}>\mathrm{bp}-\mathrm{bp}$

सहसंयोजी बंधन के प्रति वैलेंस बॉन्ड (VB) दृष्टिकोण मूलतः सहसंयोजी बंध बनने की ऊर्जा-विषयक स्थिति से संबंधित है, जिस पर लुइस और VSEPR मॉडल कुछ नहीं कहते। मूलतः VB सिद्धांत कक्षकों के अतिव्यापन के संदर्भ में बंध निर्माण की चर्चा करता है। उदाहरण के लिए दो हाइड्रोजन परमाणुओं से $\mathrm{H}_{2}$ अणु बनने में दो $\mathrm{H}$ परमाणुओं के एकल-अधिकृत $1\mathrm{~s}$ कक्षकों का अतिव्यापन होता है। यह देखा गया है कि जैसे-जैसे दो $\mathrm{H}$ परमाणु निकट आते हैं, तंत्र की स्थितिज ऊर्जा घटती है। साम्य अंतर-नाभिक दूरी (बंध दूरी) पर ऊर्जा न्यूनतम हो जाती है। नाभिकों को और भी निकट लाने का प्रयास ऊर्जा में आकस्मिक वृद्धि और अणु की अस्थिरता का कारण बनता है। कक्षक अतिव्यापन के कारण नाभिकों के बीच इलेक्ट्रॉन घनत्व बढ़ जाता है, जो उन्हें निकट लाने में सहायक होता है। यह देखा गया है कि वास्तविक बंध एन्थैल्पी और बंध लंबाई के मान अतिव्यापन से ही नहीं प्राप्त होते; अन्य चरों को भी ध्यान में रखना पड़ता है।

बहुपरमाणुक अणुओं की विशिष्ट आकृतियों की व्याख्या करने के लिए पॉलिंग ने परमाण्वीय कक्षकों के संकरण की अवधारणा प्रस्तुत की। Be, B, C, N और O के परमाण्वीय कक्षकों के $s p, s p^{2}, s p^{3}$ संकरणों का उपयोग BeCl₂, BCl₃, CH₄, NH₃ और H₂O जैसे अणुओं के निर्माण और ज्यामितीय आकृतियों की व्याख्या करने के लिए किया जाता है। ये C₂H₂ और C₂H₄ जैसे अणुओं में बहुबंधन के निर्माण की भी व्याख्या करते हैं।

आण्विक कक्षक (MO) सिद्धांत बंधन को उन परमाण्वीय कक्षकों के संयोजन और व्यवस्था के संदर्भ में वर्णित करता है जो पूरे अणु से संबद्ध आण्विक कक्षकों को बनाते हैं। आण्विक कक्षकों की संख्या हमेशा उन परमाण्वीय कक्षकों की संख्या के बराबर होती है जिनसे वे बने हैं। बंधनकारी आण्विक कक्षक नाभिकों के बीच इलेक्ट्रॉन घनत्व को बढ़ाते हैं और व्यक्तिगत परमाण्वीय कक्षकों की तुलना में कम ऊर्जा में होते हैं। प्रतिबंधनकारी आण्विक कक्षकों में नाभिकों के बीच शून्य इलेक्ट्रॉन घनत्व का क्षेत्र होता है और उनमें व्यक्तिगत परमाण्वीय कक्षकों की तुलना में अधिक ऊर्जा होती है।

अणुओं का इलेक्ट्रॉनिक विन्यास, आण्विक कक्षकों को बढ़ती ऊर्जा स्तर के क्रम में इलेक्ट्रॉन भरकर लिखा जाता है। परमाणुओं की तरह, आण्विक कक्षकों को भरने के लिए पाउली अपवर्जन सिद्धांत और हुंड नियम लागू होते हैं। अणुओं को स्थिर कहा जाता है यदि आबंधन आण्विक कक्षकों में इलेक्ट्रॉनों की संख्या प्रतिआबंधन आण्विक कक्षकों की तुलना में अधिक हो।

हाइड्रोजन बंध तब बनता है जब एक हाइड्रोजन परमाणु स्वयं को दो अत्यधिक विद्युतरासायनिक परमाणुओं, जैसे F, O और N, के बीच पाता है। यह अंतरअणुक (एक ही या विभिन्न पदार्थों के दो या अधिक अणुओं के बीच विद्यमान) या अंतःअणुक (एक ही अणु के भीतर उपस्थित) हो सकता है। हाइड्रोजन बंधों का कई यौगिकों की संरचना और गुणधर्मों पर शक्तिशाली प्रभाव पड़ता है।

CUET Preparation

CUET UG (About Exam)

CUET PG (About Exam)

Exam Pattern

CUET (UG)

CUET (PG)

International Students

Application Process

Eligibility

Exam Centres

Fees

Life In India

Middle East

Visa and Admission

NCERT Books

Class 11

Class 12

Important Resources

CUET Syllabus

Last 7 Days Preparation Strategy

Last 15 Days Preparation Strategy

Last 30 Days Preparation Strategy

Contact Us

Forum

Sathee Forum

icon  BETA

© 2014-2026 Copyright SATHEE

Privacy Policy

Powered by Prutor@IITK

sathee@iitk.ac.in
Media coverage of SATHEE
google

Play Store
apple

App Store
The Ministry of Education has launched the SATHEE initiative in association with IIT Kanpur to provide free guidance for competitive exams. SATHEE offers a range of resources, including reference video lectures, mock tests, and other resources to support your preparation. Please note that participation in the SATHEE program does not guarantee clearing any exam or admission to any institute.