कलन को एक कुंजी के रूप में प्रयोग करके, गणित को प्रकृति के प्रवाह की व्याख्या में सफलतापूर्वक लगाया जा सकता है - व्हाइटहेड

12.1 परिचय

यह अध्याय कलन का परिचय है। कलन गणित की वह शाखा है जो मुख्यतः फलन के मान में आने वाले परिवर्तन का अध्ययन करती है जैसे-जैसे डोमेन के बिंदु बदलते हैं। पहले हम अवकलज का एक सहज विचार देते हैं (बिना उसे परिभाषित किए)। फिर हम सीमा की एक सरल परिभाषा देते हैं और सीमाओं के कुछ बीजगणितीय नियमों का अध्ययन करते हैं। फिर हम वापस अवकलज की परिभाषा पर आते हैं और अवकलजों के कुछ बीजगणितीय नियमों का अध्ययन करते हैं। हम कुछ मानक फलनों के अवकलज भी प्राप्त करते हैं।

सर आइज़ेक न्यूटन (1642-1727 ई.)

12.2 अवकलजों की सहज धारणा

भौतिक प्रयोगों ने पुष्टि की है कि एक ऊँची चट्टान से गिराया गया पिंड Sir Issac Newton $(1642-1727)$ $t$ सेकंड में $4.9 t^{2}$ मीटर की दूरी तय करता है, अर्थात् समय $t$ सेकंड के फलनस्वरूप पिंड द्वारा तय की गई दूरी $s$ मीटर में $s=4.9 t^{2}$ द्वारा दी जाती है।

सटेक तालिका 13.1 एक ऊँची चट्टान से गिराए गए पिंड द्वारा सेकंडों में विभिन्न समय अंतरालों पर मीटर में तय की गई दूरी देती है।

उद्देश्य इस डेटा से $t=2$ सेकंड पर शरीर का वेग ज्ञात करना है। इस समस्या को हल करने का एक तरीका यह है कि $t=2$ सेकंड पर समाप्त होने वाले विभिन्न समय अंतरालों के लिए औसत वेग ज्ञात किया जाए और आशा की जाए कि ये $t=2$ सेकंड पर वेग के बारे में कुछ प्रकाश डालें।

$t=t_1$ और $t=t_2$ के बीच औसत वेग बराबर होता है $t=t_1$ और $t=t_2$ सेकंड के बीच तय की गई दूरी को $(t_2-t_1)$ से विभाजित करने पर। इसलिए पहले दो सेकंड में औसत वेग

$$ \begin{aligned} & =\frac{t_2=2 \text{ और } t_1=0 \text{ के बीच तय की गई दूरी}}{\text{ समय अंतर }(t_2-t_1)} \\ & =\frac{(19.6-0) m}{(2-0) s}=9.8 m / s . \end{aligned} $$

इसी प्रकार, $t=1$ और $t=2$ के बीच औसत वेग है

$$ \frac{(19.6-4.9) m}{(2-1) s}=14.7 m / s $$

इसी तरह हम विभिन्न $t_1$ के लिए $t=t_1$ और $t=2$ के बीच औसत वेग की गणना करते हैं। निम्नलिखित तालिका 13.2 औसत वेग $(v)$, $t=t_1$ सेकंड और $t=2$ सेकंड देती है।

तालिका 12.1

$t$	$s$
0	0
1	4.9
1.5	11.025
1.8	15.876
1.9	17.689
1.95	18.63225
2	19.6
2.05	20.59225
2.1	21.609
2.2	23.716
2.5	30.625
3	44.1
4	78.4

तालिका 12.2

$t_1$	0	1	1.5	1.8	1.9	1.95	1.99
$v$	9.8	14.7	17.15	18.62	19.11	19.355	19.551

टेबल 12.2 से हम देखते हैं कि औसत वेग धीरे-धीरे बढ़ रहा है। जैसे-जैसे हम $t=2$ पर समाप्त होने वाले समय अंतरालों को छोटा करते हैं, हमें $t=2$ पर वेग का बेहतर अनुमान मिलता है। यह आशा करते हुए कि 1.99 सेकंड और 2 सेकंड के बीच कुछ असाधारण नहीं होता है, हम निष्कर्ष निकालते हैं कि $t=2$ सेकंड पर औसत वेग $19.551 m / s$ से थोड़ा ऊपर है।

यह निष्कर्ष निम्नलिखित गणनाओं के समूह द्वारा कुछ मजबूत हो जाता है। $t=2$ सेकंड से शुरू होने वाले विभिन्न समय अंतरालों के लिए औसत वेग की गणना करें। जैसे पहले, $t=2$ सेकंड और $t=t_2$ सेकंड के बीच औसत वेग $v$ है

$ \begin{aligned} & =\frac{\text{ 2 सेकंड और } t_2 \text{ सेकंड के बीच तय की गई दूरी }}{t_2-2} \\ & =\frac{t_2 \text{ सेकंड में तय की गई दूरी }- \text{ 2 सेकंड में तय की गई दूरी }}{t_2-2} \end{aligned} $

$ =\frac{t_2 \text{ सेकंड में तय की गई दूरी }-19.6}{t_2-2} $

निम्नलिखित टेबल 12.3, $t=2$ सेकंड और $t_2$ सेकंड के बीच औसत वेग $v$ को मीटर प्रति सेकंड में देता है।

टेबल 12.3

$t_2$	4	3	2.5	2.2	2.1	2.05	2.01
$v$	29.4	24.5	22.05	20.58	20.09	19.845	19.649

यहाँ फिर हम देखते हैं कि यदि हम $t=2$ से शुरू होने वाले समय अंतरालों को छोटा करते हैं, तो हमें $t=2$ पर वेग का बेहतर अनुमान मिलता है।

पहली गणनाओं के समूह में, हमने यह किया है कि $t=2$ पर समाप्त होने वाले बढ़ते हुए समय अंतरालों में औसत वेग ज्ञात किए और फिर आशा की कि $t=2$ से ठीक पहले कुछ भी नाटकीय नहीं होता। दूसरी गणनाओं के समूह में, हमने $t=2$ पर समाप्त होने वाले घटते समय अंतरालों में औसत वेग ज्ञात किए और फिर आशा की कि $t=2$ के ठीक बाद कुछ भी नाटकीय नहीं होता। केवल भौतिक आधार पर, इन दोनों औसत वेगों की अनुक्रम एक सामान्य सीमा की ओर अग्रसर होना चाहिए। हम सुरक्षित रूप से निष्कर्ष निकाल सकते हैं कि $t=2$ पर पिण्ड का वेग $19.551 m / s$ और $19.649 m / s$ के बीच है। तकनीकी रूप से, हम कहते हैं कि $t=2$ पर तात्कालिक वेग $19.551 m / s$ और $19.649 m / s$ के बीच है। जैसा कि सुप्रसिद्ध है, वेग विस्थापन के परिवर्तन की दर होता है। इसलिए हमने जो प्राप्त किया है वह निम्नलिखित है। विभिन्न समय क्षणों पर तय की गई दूरी के दिए गए आँकड़ों से हमने एक निर्धारित समय क्षण पर दूरी की परिवर्तन दर का आकलन किया है। हम कहते हैं कि दूरी फलन $s=4.9 t^{2}$ का $t=2$ पर अवकलज 19.551 और 19.649 के बीच है।

इस सीमाबद्ध प्रक्रिया को देखने का एक वैकल्पिक तरीका आकृति 12.1 में दिखाया गया है। यह चट्टान के शीर्ष से पिण्ड की दूरी $s$ का बीते हुए समय $t$ के सापेक्ष आरेख है। सीमा में, जैसे-जैसे समय अंतरालों का अनुक्रम $h_1, h_2, \ldots$, शून्य की ओर अग्रसर होता है, औसत वेगों का अनुक्रम उसी सीमा की ओर अग्रसर होता है जिस ओर अनुपातों का अनुक्रम

आकृति 12.1

$ \frac{C_1 B_1}{AC_1}, \frac{C_2 B_2}{AC_2}, \frac{C_3 B_3}{AC_3}, \ldots $

जहाँ $C_1 B_1=s_1-s_0$ समय अंतराल $h_1=AC_1$ में शरीर द्वारा तय की गई दूरी है, आदि। आकृति 12.1 से यह सुरक्षित रूप से निष्कर्ष निकाला जा सकता है कि यह बाद वाला क्रम बिंदु $A$ पर वक्र की स्पर्श रेखा की ढाल के निकट आता है। दूसरे शब्दों में, समय $t=2$ पर शरीर का तात्कालिक वेग $v(t)$ वक्र $s=4.9 t^{2}$ की स्पर्श रेखा की ढाल के बराबर है जब $t=2$।

12.3 सीमाएँ

उपरोक्त चर्चा स्पष्ट रूप से इस तथफ की ओर इशारा करती है कि हमें सीमित प्रक्रिया को अधिक स्पष्टता से समझने की आवश्यकता है। हम सीमाओं की अवधारणा के साथ कुछ परिचय प्राप्त करने के लिए कुछ व्याख्यात्मक उदाहरणों का अध्ययन करते हैं।

फलन $f(x)=x^{2}$ पर विचार करें। ध्यान दें कि जैसे ही $x$ 0 के बहुत निकट मान लेता है, $f(x)$ का मान भी 0 की ओर बढ़ता है (देखें आकृति 2.10 अध्याय 2)। हम कहते हैं

$ \begin{aligned} \lim\limits_{x \to 0} f(x)=0 \end{aligned} $

(इसे $x$ शून्य की ओर जाता है पर $f(x)$ की सीमा शून्य के बराबर है के रूप में पढ़ा जाता है)। $f(x)$ की सीमा जैसे $x$ शून्य की ओर जाता है को इस मान के रूप में सोचा जाना चाहिए जो $f(x)$ को $x=0$ पर ग्रहण करना चाहिए।

सामान्य रूप से जैसे $x \to a, f(x) \to l$, तब $l$ को फलन $f(x)$ की सीमा कहा जाता है जिसे प्रतीकात्मक रूप से $\lim\limits_{x \to a} f(x)=l$ लिखा जाता है।

निम्नलिखित फलन पर विचार कीजिए $g(x)=|x|, x \neq 0$। ध्यान दीजिए कि $g(0)$ परिभाषित नहीं है। $x$ के ऐसे मानों के लिए $g(x)$ का मान निकालिए जो 0 के बहुत निकट हैं, हम देखते हैं कि $g(x)$ का मान 0 की ओर बढ़ता है। इसलिए, $\lim\limits_{x \to 0} g(x)=0$। यह सहज रूप से $x \neq 0$ के लिए $y=|x|$ के ग्राफ से स्पष्ट है। (देखिए अध्याय 2 की आकृति 2.13)।

निम्नलिखित फलन पर विचार कीजिए।

$ h(x)=\frac{x^{2}-4}{x-2}, x \neq 2 $

$x$ के ऐसे मानों के लिए $h(x)$ का मान निकालिए जो 2 के बहुत निकट हैं (लेकिन 2 पर नहीं)। स्वयं को यह विश्वास दिलाइए कि ये सभी मान 4 के निकट हैं। यह यहाँ दिए गए फलन $y=h(x)$ के ग्राफ पर विचार करने से कुछ हद तक और मजबूत हो जाता है (आकृति 12.2)।

आकृति 12.2

इन सभी उदाहरणों में किसी दिए गए बिंदु $x=a$ पर फलन को जो मान लेना चाहिए था, वह वास्तव में इस बात पर निर्भर नहीं करता था कि $x$, $a$ की ओर कैसे बढ़ रहा है। ध्यान दीजिए कि $x$ किसी संख्या $a$ की ओर अनिवार्य रूप से दो तरीकों से बढ़ सकता है — या तो बाएँ से या दाएँ से, अर्थात् $a$ के निकट के सभी $x$ के मान $a$ से छोटे हो सकते हैं या $a$ से बड़े हो सकते हैं। यह स्वाभाविक रूप से दो सीमाओं की ओर ले जाता है — दाहिनी सीमा और बायीं सीमा। किसी फलन $f(x)$ की दाहिनी सीमा वह मान है जो $f(x)$ के उन मानों द्वारा निर्धारित होता है जब $x$, $a$ की ओर दाहिनी ओर से बढ़ता है। इसी प्रकार, बायीं सीमा। इसे स्पष्ट करने के लिए, फलन पर विचार कीजिए

$ f(x)= \begin{cases}1, & x \leq 0 \\ 2, & x>0\end{cases} $

इस फलन का ग्राफ चित्र 12.3 में दिखाया गया है। यह स्पष्ट है कि 0 पर f का मान, x ≤ 0 के f(x) के मानों द्वारा निर्धारित होता है जो 1 के बराबर है, अर्थात् 0 पर f(x) का बायाँ पक्ष सीमा है $ \lim\limits_{x \to 0} f(x)=1 . $

इसी प्रकार, 0 पर f का मान, x>0 के f(x) के मानों द्वारा निर्धारित होता है जो 2 के बराबर है, अर्थात् 0 पर f(x) का दायाँ पक्ष सीमा है

$ \lim\limits_{x \to 0^{+}} f(x)=2 . $

इस स्थिति में दायाँ और बायाँ पक्ष सीमाएँ भिन्न हैं, और इसलिए हम कहते हैं कि x के शून्य की ओर जाते समय f(x) की सीमा अस्तित्व में नहीं होती (यद्यपि फलन 0 पर परिभाषित है)।

सारांश

हम कहते हैं कि $\lim\limits_{x \to a^{-}} f(x)$, a के बायीं ओर x के f के मानों को देखते हुए x=a पर f का अपेक्षित मान है। इस मान को a पर f की बायाँ पक्ष सीमा कहा जाता है।

हम कहते हैं कि $\lim\limits_{x \to a^{+}} f(x)$, a के दायीं ओर x के f के मानों को देखते हुए x=a पर f का अपेक्षित मान है। इस मान को a पर f(x) की दायाँ पक्ष सीमा कहा जाता है।

यदि दायाँ और बायाँ पक्ष सीमाएँ मेल खाती हैं, तो हम उस सामान्य मान को x=a पर f(x) की सीमा कहते हैं और इसे $\lim\limits_{x \to a} f(x)$ द्वारा दर्शाते हैं।

चित्रण 1 फलन $f(x)=x+10$ पर विचार करें। हम इस फलन का सीमा $x=5$ पर ज्ञात करना चाहते हैं। आइए $x$ के 5 के बहुत निकट होने पर फलन $f(x)$ का मान परिकलित करें। 5 के बाईं ओर और निकट कुछ बिंदु 4.9, 4.95, 4.99, 4.995 … आदि हैं। इन बिंदुओं पर फलन के मान नीचे सारणीबद्ध किए गए हैं। इसी प्रकार, वास्तविक संख्या 5.001, 5.01, 5.1 भी 5 के निकट और दाईं ओर के बिंदु हैं। इन बिंदुओं पर फलन के मान भी सारणी 12.4 में दिए गए हैं।

सारणी 12.4

$x$	4.9	4.95	4.99	4.995	5.001	5.01	5.1
$f(x)$	14.9	14.95	14.99	14.995	15.001	15.01	15.1

सारणी 12.4 से हम निष्कर्ष निकालते हैं कि $x=5$ पर $f(x)$ का मान 14.995 से अधिक और 15.001 से कम होना चाहिए, यह मानकर कि $x=4.995$ और 5.001 के बीच कुछ भी असामान्य नहीं होता है। यह मानना तर्कसंगत है कि 5 के बाईं ओर की संख्याओं द्वारा निर्दिष्ट $x=5$ पर $f(x)$ का मान 15 है, अर्थात्

$$ \lim\limits_{x \to 5^{-}} f(x)=15 . $$

इसी प्रकार, जब $x$ दाईं ओर से 5 की ओर बढ़ता है, तो $f(x)$ को मान 15 लेना चाहिए, अर्थात्

$$ \lim\limits_{x \to 5^{+}} f(x)=15 \text{. } $$

इसलिए, यह संभावना है कि $f(x)$ का बायाँ पक्ष सीमा और दायाँ पक्ष सीमा दोनों 15 के बराबर हैं। इस प्रकार,

$$ \lim\limits_{x \to 5^{-}} f(x)=\lim\limits_{x \to 5^{+}} f(x)=\lim\limits_{x \to 5} f(x)=15 . $$

इस निष्कर्ष की पुष्टि कि सीमा 15 के बराबर है, इस फलन के आलेख को देखने से और भी मज़बूत होती है, जो कि चित्र 2.16, अध्याय 2 में दिया गया है। इस चित्र में हम देखते हैं कि जैसे-जैसे $x$ दाएँ या बाएँ से 5 के पास पहुँचता है, फलन $f(x)=x+10$ का आलेख बिंदु $(5,15)$ की ओर बढ़ता है।

हम देखते हैं कि $x=5$ पर फलन का मान भी संयोगवश 15 के बराबर है।

उदाहरण 2 फलन $f(x)=x^{3}$ पर विचार करें। आइए इस फलन की सीमा $x=1$ पर ज्ञात करने का प्रयास करें। पिछले उदाहरण की भाँति आगे बढ़ते हुए, हम $x$ के 1 के पास के मानों पर $f(x)$ के मानों को सारणीबद्ध करते हैं। यह सारणी 12.5 में दिया गया है।

सारणी 12.5

$x$	0.9	0.99	0.999	1.001	1.01	1.1
$f(x)$	0.729	0.970299	0.997002999	1.003003001	1.030301	1.331

इस सारणी से हम यह निष्कर्ष निकालते हैं कि $x=1$ पर $f(x)$ का मान 0.997002999 से अधिक और 1.003003001 से कम होना चाहिए, यह मान लेते हुए कि $x=0.999$ और 1.001 के बीच कुछ असामान्य नहीं होता। यह मान लेना तर्कसंगत है कि 1 के बाईं ओर के अंकों द्वारा निर्धारित $x=1$ पर $f(x)$ का मान 1 है, अर्थात्

$$ \lim\limits_{x \to 1^{-}} f(x)=1 \text{. } $$

इसी प्रकार, जब $x$ दाएँ से 1 की ओर बढ़ता है, तो $f(x)$ का मान 1 होना चाहिए, अर्थात्

$$ \lim\limits_{x \to 1^{+}} f(x)=1 \text{. } $$

इस प्रकार, यह संभावना है कि $f(x)$ का बायाँ पक्ष सीमा और दायाँ पक्ष सीमा दोनों 1 के बराबर हैं। इस प्रकार,

$$ \lim\limits_{x \to 1^{-}} f(x)=\lim\limits_{x \to 1^{+}} f(x)=\lim\limits_{x \to 1} f(x)=1 . $$

इस निष्कर्ष कि सीमा 1 के बराबर है, को कुछ हद तक मजबूती इस फलन के आलेख को देखकर मिलती है, जो कि अध्याय 2 की आकृति 2.11 में दिया गया है। इस आकृति में हम देखते हैं कि जब $x$ बाएँ या दाएँ से 1 के पास आता है, तो फलन $f(x)=x^{3}$ का आलेख बिंदु $(1,1)$ की ओर बढ़ता है।

हम पुनः देखते हैं कि $x=1$ पर फलन का मान भी संयोगवश 1 के बराबर है।

उदाहरण 3 फलन $f(x)=3 x$ पर विचार करें। आइए इस फलन की सीमा $x=2$ पर ज्ञात करने का प्रयास करें। निम्नलिखित सारणी 12.6 अब स्वतः स्पष्ट है।

सारणी 12.6

$x$	1.9	1.95	1.99	1.999	2.001	2.01	2.1
$f(x)$	5.7	5.85	5.97	5.997	6.003	6.03	6.3

जैसा पहले, हम देखते हैं कि जब $x$ बाएँ या दाएँ से 2 के पास आता है, तो $f(x)$ का मान 6 की ओर प्रतीत होता है। हम इसे इस प्रकार लिखते हैं

$$ \lim\limits_{x \to 2^{-}} f(x)=\lim\limits_{x \to 2^{+}} f(x)=\lim\limits_{x \to 2} f(x)=6 $$

इसका आलेख, जो आकृति 12.4 में दिखाया गया है, इस तथ्य को पुष्ट करता है।

आकृति 12.4

यहाँ पुनः हम देखते हैं कि $x=2$ पर फलन का मान, $x=2$ पर सीमा के साथ मेल खाता है।

चित्रण 4 निरंतर फलन $f(x)=3$ पर विचार करें। आइए इसका सीमा $x=2$ पर ज्ञात करने का प्रयास करें। यह फलन एक निरंतर फलन होने के कारण हर जगह समान मान (इस मामले में 3) लेता है, अर्थात् 2 के निकट बिंदुओं पर इसका मान 3 है। इसलिए

$ \lim\limits_{x \to 2} f(x)=\lim\limits_{x \to 2^{+}} f(x)=\lim\limits_{x \to 2} f(x)=3 $

$f(x)=3$ का आलेख वैसे भी $x$-अक्ष के समानांतर $(0,3)$ से गुजरने वाली रेखा है और इसे अध्याय 2 में आकृति 2.9 में दिखाया गया है। इससे भी यह स्पष्ट है कि अभीष्ट सीमा 3 है। वास्तव में, यह आसानी से देखा जा सकता है कि किसी भी वास्तविक संख्या $a$ के लिए $\lim\limits_{x \to a} f(x)=3$ है।

चित्रण 5 फलन $f(x)=x^{2}+x$ पर विचार करें। हम $\lim\limits_{x \to 1} f(x)$ ज्ञात करना चाहते हैं। हम तालिका 12.7 में $x=1$ के निकट $f(x)$ के मानों को सारणीबद्ध करते हैं।

तालिका 12.7

$x$	0.9	0.99	0.999	1.01	1.1	1.2
$f(x)$	1.71	1.9701	1.997001	2.0301	2.31	2.64

इससे यह तर्कसंगत रूप से निष्कर्ष निकाला जा सकता है कि $\lim\limits_{x \to 1^{-}} f(x)=\lim\limits_{x \to 1^{+}} f(x)=\lim\limits_{x \to 1} f(x)=2$।

आकृति 12.5 में दिखाए गए $f(x)=x^{2}+x$ के आलेख से यह स्पष्ट है कि जैसे-जैसे $x$, 1 के निकट आता है, आलेख $(1,2)$ के निकट आता है।

आकृति 12.5

यहाँ, हम फिर से देखते हैं कि

$ \lim\limits_{x \to 1} f(x)=f(1) $

अब, निम्नलिखित तीन तथ्यों को स्वयं सुनिश्चित करें:

$ \lim\limits_{x \to 1} x^{2}=1, \lim\limits_{x \to 1} x=1 \text{ और } \lim\limits_{x \to 1} x+1=2 $

तब $ \quad\quad\quad\quad \lim\limits_{x \to 1} x^{2}+\lim\limits_{x \to 1} x=1+1=2=\lim\limits_{x \to 1}[x^{2}+x] \text{. } $

साथ ही $ \quad\quad\quad\quad\lim\limits_{x \to 1} x . \lim\limits_{x \to 1}(x+1)=1 \cdot 2=2=\lim\limits_{x \to 1}[x(x+1)]=\lim\limits_{x \to 1}[x^{2}+x] . $

उदाहरण 6 फलन $f(x)=\sin x$ पर विचार करें। हमें $\lim\limits_{x \to \frac{\pi}{2}} \sin x$ में रुचि है, जहाँ कोण रेडियन में मापा जाता है।

यहाँ, हम $\frac{\pi}{2}$ के निकट $f(x)$ का (अनुमानित) मान सारणीबद्ध करते हैं (सारणी 12.8)। इससे हम यह निष्कर्ष निकाल सकते हैं कि

$ \lim\limits_{x \to \frac{\pi^{-}}{2}} f(x)=\lim\limits_{x \to \frac{\pi^{+}}{2}} f(x)=\lim\limits_{x \to \frac{\pi}{2}} f(x)=1 $

इसके अतिरिक्त, यह $f(x)=\sin x$ के आलेख द्वारा समर्थित है जो कि आकृति 3.8 (अध्याय 3) में दिया गया है। इस स्थिति में भी, हम देखते हैं कि $\lim\limits_{x \to \frac{\pi}{2}} \sin x=1$।

सारणी 12.8

$x$	$\frac{\pi}{2}-0.1$	$\frac{\pi}{2}-0.01$	$\frac{\pi}{2}+0.01$	$\frac{\pi}{2}+0.1$
$f(x)$	0.9950	0.9999	0.9999	0.9950

उदाहरण 7 फलन $f(x)=x+\cos x$ पर विचार करें। हमें $\lim\limits_{x \to 0} f(x)$ ज्ञात करना है। यहाँ हम 0 के निकट $f(x)$ का (अनुमानित) मान सारणीबद्ध करते हैं (सारणी 12.9)।

सारणी 12.9

$x$	-0.1	-0.01	-0.001	0.001	0.01	0.1
$f(x)$	0.9850	0.98995	0.9989995	1.0009995	1.00995	1.0950

तालिका 12.9 से हम यह निष्कर्ष निकाल सकते हैं कि

$ \lim\limits_{x \to 0^{-}} f(x)=\lim\limits_{x \to 0^{+}} f(x)=\lim\limits_{x \to 0} f(x)=1 $

इस स्थिति में भी, हम देखते हैं कि $\lim\limits_{x \to 0} f(x)=f(0)=1$।

अब, क्या आप स्वयं को यह विश्वास दिला सकते हैं कि

$ \lim\limits_{x \to 0}[x+\cos x]=\lim\limits_{x \to 0} x+\lim\limits_{x \to 0} \cos x \text{ वास्तव में सत्य है? } $

उदाहरण 8 फलन $f(x)=\frac{1}{x^{2}}$ को $x>0$ के लिए लीजिए। हम जानना चाहते हैं कि $\lim\limits_{x \to 0} f(x)$ क्या है।

यहाँ, ध्यान दीजिए कि फलन का प्रांत सभी धनात्मक वास्तविक संख्याओं के लिए दिया गया है। इसलिए, जब हम $f(x)$ के मानों की सारणी बनाते हैं, तो $x$ के 0 से बाईं ओर आने की बात करना कोई अर्थ नहीं रखता। नीचे हम 0 के निकट धनात्मक $x$ के लिए फलन के मानों की सारणी बना रहे हैं (इस सारणी में $n$ कोई धनात्मक पूर्णांक दर्शाता है)।

नीचे दी गई तालिका 12.10 से हम देखते हैं कि जैसे-जैसे $x$ का मान 0 की ओर जाता है, $f(x)$ बड़ा और बड़ा होता जाता है। हमारा तात्पर्य यह है कि $f(x)$ का मान किसी भी दी गई संख्या से बड़ा किया जा सकता है।

तालिका 12.10

$x$	1	0.1	0.01	$10^{-n}$
$f(x)$	1	100	10000	$10^{2 n}$

गणितीय रूप से, हम कहते हैं

$ \lim\limits_{x \to 0} f(x)=+\infty $

हम यह भी टिप्पणी करते हैं कि इस पाठ्यक्रम में हम ऐसी सीमाओं का सामना नहीं करेंगे।

उदाहरण 9 हम $\lim\limits_{x \to 0} f(x)$ ज्ञात करना चाहते हैं, जहाँ

$ f(x)= \begin{cases}x-2, & x<0 \\ 0, & x=0 \\ x+2, & x>0\end{cases} $

हमेशा की तरह हम 0 के पास $x$ और $f(x)$ का एक सारणी बनाते हैं। ध्यान दें कि $x$ के ऋणात्मक मानों के लिए हमें $x-2$ का मान निकालना है और धनात्मक मानों के लिए हमें $x+2$ का मान निकालना है।

सारणी 12.11

$x$	-0.1	-0.01	-0.001	0.001	0.01	0.1
$f(x)$	-2.1	-2.01	-2.001	2.001	2.01	2.1

सारणी 12.11 की पहली तीन प्रविष्टियों से हम यह निष्कर्ष निकालते हैं कि फलन का मान -2 की ओर घट रहा है और इसलिए

$$ \lim\limits_{x \to 0^{-}} f(x)=-2 $$

सारणी की अंतिम तीन प्रविष्टियों से हम यह निष्कर्ष निकालते हैं कि फलन का मान 2 से बढ़ रहा है और इसलिए

$$ \lim\limits_{x \to 0^{+}} f(x)=2 $$

चूँकि 0 पर बायाँ और दायाँ सीमा मेल नहीं खाते, हम कहते हैं कि 0 पर फलन की सीमा अस्तित्व में नहीं है।

इस फलन का ग्राफ Fig12.6 में दिया गया है। यहाँ हम यह टिप्पणी करते हैं कि $x=0$ पर फलन का मान अच्छी तरह परिभाषित है और वास्तव में 0 के बराबर है, लेकिन $x=0$ पर फलन की सीमा परिभाषित भी नहीं है।

उदाहरण 10 अंतिम उदाहरण के रूप में, हम $\lim\limits_{x \to 1} f(x)$ ज्ञात करते हैं,

जहाँ

$$ f(x)=\begin{cases} x+2 & x \neq 1 \\ 0 & x=1 \end{cases} $$

सारणी 12.12

$x$	0.9	0.99	0.999	1.001	1.01	1.1
$f(x)$	2.9	2.99	2.999	3.001	3.01	3.1

जैसा कि प्रायः हम $x$ के 1 के निकट मानों के लिए $f(x)$ के मानों को सारणीबद्ध करते हैं। $x$ के 1 से कम मानों के लिए $f(x)$ के मानों से ऐसा प्रतीत होता है कि फलन को $x=1$ पर मान 3 लेना चाहिए, अर्थात्

$ \lim\limits_{x \to 1^{-}} f(x)=3 . $

इसी प्रकार, $x$ के 1 से अधिक मानों के $f(x)$ के मानों द्वारा निर्दिष्ट किया जाता है कि $f(x)$ का मान 3 होना चाहिए। अर्थात्

$ \lim\limits_{x \to 1^{+}} f(x)=3 . $

परंतु तब बायाँ और दायाँ पक्ष सीमाएँ मेल खाती हैं और इसलिए

$ \lim\limits_{x \to 1^{-}} f(x)=\lim\limits_{x \to 1^{+}} f(x)=\lim\limits_{x \to 1} f(x)=3 . $

चित्र 12.7 में दिए गए फलन का आलेख हमारी सीमा के बारे में की गई निष्कर्षण को पुष्ट करता है। यहाँ, हम नोट करते हैं कि सामान्यतः, किसी दिए गए बिंदु पर फलन का मान और उसकी सीमा भिन्न हो सकते हैं (जब दोनों परिभाषित हों)।

चित्र 12.7

12.3.1 सीमाओं का बीजगणित

उपरोक्त उदाहरणों में, हमने देखा है कि सीमाकरण प्रक्रिया योग, व्यवकलन, गुणा और भाग को सम्मान देती है जब तक कि सीमाएँ और विचाराधीन फलन सुपरिभाषित हैं। यह संयोग नहीं है। वास्तव में, नीचे हम इन्हें एक प्रमेय के रूप में बिना प्रमाण के औपचारिक रूप देते हैं।

प्रमेय 1 मान लीजिए $f$ और $g$ दो फलन इस प्रकार हैं कि $\lim\limits_{x \to a} f(x)$ और $\lim\limits_{x \to a} g(x)$ दोनों अस्तित्व में हैं। तब

(i) दो फलनों के योग की सीमा, फलनों की सीमाओं के योग के बराबर होती है, अर्थात्

$ \lim\limits_{x \to a}[f(x)+g(x)]=\lim\limits_{x \to a} f(x)+\lim\limits_{x \to a} g(x) . $

(ii) दो फलनों के अंतर की सीमा, फलनों की सीमाओं के अंतर के बराबर होती है, अर्थात्

$ \lim\limits_{x \to a}[f(x)-g(x)]=\lim\limits_{x \to a} f(x)-\lim\limits_{x \to a} g(x) . $

(iii) दो फलनों के गुणनफल की सीमा, फलनों की सीमाओं के गुणनफल के बराबर होती है, अर्थात्

$ \lim\limits_{x \to a}[f(x) \cdot g(x)]=\lim\limits_{x \to a} f(x) . \lim\limits_{x \to a} g(x) . $

(iv) दो फलनों के भागफल की सीमा, फलनों की सीमाओं के भागफल के बराबर होती है (जब तक हर शून्य न हो), अर्थात्

$ \lim\limits_{x \to a} \frac{f(x)}{g(x)}=\frac{\lim\limits_{x \to a} f(x)}{\lim\limits_{x \to a} g(x)} $

नोट - विशेष रूप से (iii) के एक विशेष स्थिति के रूप में, जब $g$ एक नियत फलन इस प्रकार है कि $g(x)=\lambda$, किसी वास्तविक संख्या $\lambda$ के लिए, हम पाते हैं

$ \lim\limits_{x \to a}[(\lambda \cdot f)(x)]=\lambda \cdot \lim\limits_{x \to a} f(x) . $

अगले दो उप-अनुभागों में, हम दिखाते हैं कि इस प्रमेय का उपयोग करके विशेष प्रकार के फलनों की सीमाओं का मान कैसे निकाला जाता है।

12.3.2 बहुपदों और परिमेय फलनों की सीमाएँ

एक फलन (f) को (n) घात का बहुपद फलन कहा जाता है (f(x)=a_0+a_1 x+a_2 x^{2}+\ldots+a_n x^{n}), जहाँ (a_1) वास्तविक संख्याएँ हैं इस प्रकार कि (a_n \neq 0) किसी प्राकृत संख्या (n) के लिए।

हम जानते हैं कि (\lim\limits_{x \to a} x=a\। इसलिए

$ \lim\limits_{x \to a} x^{2}=\lim\limits_{x \to a}(x \cdot x)=\lim\limits_{x \to a} x \cdot \lim\limits_{x \to a} x=a \cdot a=a^{2} $

(n) पर आगमन का एक सरल अभ्यास हमें बताता है कि

$ \lim\limits_{x \to a} x^{n}=a^{n} $

अब, मान लीजिए (f(x)=a_0+a_1 x+a_2 x^{2}+\ldots+a_n x^{n}) एक बहुपद फलन है। (a_0, a_1 x, a_2 x^{2}, \ldots, a_n x^{n}) में से प्रत्येक को एक फलन के रूप में सोचते हुए, हमारे पास है

$ \begin{aligned} \lim\limits_ {x \to a} f(x) & =\lim\limits_ {x \to a}[a_ 0+a_ 1 x+a_ 2 x^{2}+\ldots+a_ {n} x^{n}] \ & =\lim\limits_ {x \to a} a_ 0+\lim\limits_ {x \to a} a_ 1 x+\lim\limits_ {x \to a} a_ 2 x^{2}+\ldots+\lim\limits_ {x \to a} a_ {n} x^{n} \ & =a_ 0+a_ 1 \lim\limits_ {x \to a} x+a_ 2 \lim\limits_ {x \to a} x^{2}+\ldots+a_ {n} \lim\limits_ {x \to a} x^{n} \ & =a_ 0+a_ 1 a+a_ 2 a^{2}+\ldots+a_ {n} a^{n} \ & =f(a) \end{aligned} $

(सुनिश्चित करें कि आप ऊपर दिए गए प्रत्येक चरण के औचित्य को समझते हैं!)

एक फलन (f) को परिमेय फलन कहा जाता है, यदि (f(x)=\frac{g(x)}{h(x)}), जहाँ (g(x)) और (h(x)) बहुपद हैं इस प्रकार कि (h(x) \neq 0). तब

$ \lim\limits_{x \to a} f(x)=\lim\limits_{x \to a} \frac{g(x)}{h(x)}=\frac{\lim\limits_{x \to a} g(x)}{\lim\limits_{x \to a} h(x)}=\frac{g(a)}{h(a)} $

हालांकि, यदि $h(a)=0$, तो दो परिदृश्य होते हैं - (i) जब $g(a) \neq 0$ और (ii) जब $g(a)=0$। पहले मामले में हम कहते हैं कि सीमा अस्तित्व में नहीं है। बाद के मामले में हम $g(x)=(x-a)^{k} g_1(x)$ लिख सकते हैं, जहाँ $k$ गुणांक $(x-a)$ की अधिकतम घात है जो $g(x)$ में है। इसी प्रकार, $h(x)=(x-a)^{l} h_1(x)$ क्योंकि $h(a)=0$। अब, यदि $k>l$, तो हमारे पास

$ \lim\limits_{x \to a} f(x)=\frac{\lim\limits_{x \to a} g(x)}{\lim\limits_{x \to a} h(x)}=\frac{\lim\limits_{x \to a}(x-a)^{k} g_1(x)}{\lim\limits_{x \to a}(x-a)^{l} h_1(x)} $

$ =\frac{\lim\limits_{x \to a}(x-a)^{(k-l)} g_1(x)}{\lim\limits_{x \to a} h_1(x)}=\frac{0 . g_1(a)}{h_1(a)}=0 $

यदि $k<l$, तो सीमा परिभाषित नहीं है।

उदाहरण 1 सीमाएँ ज्ञात कीजिए:

(i) $\lim\limits_{x \to 1}[x^{3}-x^{2}+1] \quad$

(ii) $\lim\limits_{x \to 3}[x(x+1)]$

(iii) $\lim\limits_{x \to-1}[1+x+x^{2}+\ldots+x^{10}]$.

हल आवश्यक सीमाएँ कुछ बहुपद फलनों की सीमाएँ हैं। इसलिए सीमाएँ निर्धारित बिंदुओं पर फलन के मान हैं। हमारे पास

(i) $\lim\limits_{x \to 1}[x^{3}-x^{2}+1]=1^{3}-1^{2}+1=1$

(ii) $\lim\limits_{x \to 3}[x(x+1)]=3(3+1)=3(4)=12$

(iii) $\lim\limits_{x \to-1}[1+x+x^{2}+\ldots+x^{10}]=1+(-1)+(-1)^{2}+\ldots+(-1)^{10}$

उदाहरण 2 सीमाएँ ज्ञात कीजिए:

(i) $\lim\limits_{x \to 1}[\frac{x^{2}+1}{x+100}]$

(ii) $\lim\limits_{x \to 2}[\frac{x^{3}-4 x^{2}+4 x}{x^{2}-4}]$

(iii) $\lim\limits_{x \to 2}[\frac{x^{2}-4}{x^{3}-4 x^{2}+4 x}]$

(iv) $\lim\limits_{x \to 2}[\frac{x^{3}-2 x^{2}}{x^{2}-5 x+6}]$

(v) $\lim\limits_{x \to 1}[\frac{x-2}{x^{2}-x}-\frac{1}{x^{3}-3 x^{2}+2 x}]$.

हल विचाराधीन सभी फलन परिमेय फलन हैं। इसलिए, हम पहले इन फलनों को निर्धारित बिंदुओं पर मानते हैं। यदि यह $\frac{0}{0}$ के रूप में है, तो हम फलन को पुनः लिखने का प्रयास करते हैं जिससे वे गुणनफल समाप्त हो जाएँ जो सीमा को $\frac{0}{0}$ के रूप में बनाने के लिए उत्तरदायी हैं।

(i) हमारे पास $\lim\limits_{x \to 1} \frac{x^{2}+1}{x+100}=\frac{1^{2}+1}{1+100}=\frac{2}{101}$ है।

(ii) फलन को 2 पर मानते समय, यह $\frac{0}{0}$ के रूप में है।

इसलिए $\lim\limits_{x \to 2} \frac{x^{3}-4 x^{2}+4 x}{x^{2}-4}=\lim\limits_{x \to 2} \frac{x(x-2)^{2}}{(x+2)(x-2)}$

$ \begin{aligned} & =\lim\limits_{x \to 2} \frac{x(x-2)}{(x+2)} \quad \quad \quad \quad \text{चूँकि } x \neq 2 \\ & =\frac{2(2-2)}{2+2}=\frac{0}{4}=0 . \end{aligned} $

(iii) फलन को 2 पर मानते समय, हमें यह $\frac{0}{0}$ के रूप में मिलता है।

इसलिए $\lim\limits_{x \to 2} \frac{x^{2}-4}{x^{3}-4 x^{2}+4 x}=\lim\limits_{x \to 2} \frac{(x+2)(x-2)}{x(x-2)^{2}}$

$ =\lim\limits_{x \to 2} \frac{(x+2)}{x(x-2)}=\frac{2+2}{2(2-2)}=\frac{4}{0} $

जो परिभाषित नहीं है।

(iv) फलन को 2 पर मानते समय, हमें यह $\frac{0}{0}$ के रूप में मिलता है।

इसलिए $\quad \lim\limits_{x \to 2} \frac{x^{3}-2 x^{2}}{x^{2}-5 x+6}=\lim\limits_{x \to 2} \frac{x^{2}(x-2)}{(x-2)(x-3)}$

$ =\lim\limits_{x \to 2} \frac{x^{2}}{(x-3)}=\frac{(2)^{2}}{2-3}=\frac{4}{-1}=-4 . $

(v) पहले, हम फलन को एक परिमेय फलन के रूप में पुनः लिखते हैं।

$ \begin{aligned} {[\frac{x-2}{x^{2}-x}-\frac{1}{x^{3}-3 x^{2}+2 x}] } & =[\frac{x-2}{x(x-1)}-\frac{1}{x(x^{2}-3 x+2)}] \\ & =[\frac{x-2}{x(x-1)}-\frac{1}{x(x-1)(x-2)}] \\ & =[\frac{x^{2}-4 x+4-1}{x(x-1)(x-2)}] \\ & =\frac{x^{2}-4 x+3}{x(x-1)(x-2)} \end{aligned} $

फंक्शन को 1 पर मूल्यांकित करने पर हमें $\frac{0}{0}$ के रूप में प्राप्त होता है।

इसलिए $\quad \lim\limits_{x \to 1}[\frac{x^{2}-2}{x^{2}-x}-\frac{1}{x^{3}-3 x^{2}+2 x}]=\lim\limits_{x \to 1} \frac{x^{2}-4 x+3}{x(x-1)(x-2)}$

$ \begin{aligned} & =\lim\limits_{x \to 1} \frac{(x-3)(x-1)}{x(x-1)(x-2)} \\ & =\lim\limits_{x \to 1} \frac{x-3}{x(x-2)}=\frac{1-3}{1(1-2)}=2 . \end{aligned} $

हम टिप्पणी करते हैं कि हम ऊपर के मूल्यांकन में पद $(x-1)$ को रद्द कर सकते थे क्योंकि $x \neq 1$।

एक महत्वपूर्ण सीमा का मूल्यांकन जो आगे चलकर उपयोग में आएगा, नीचे प्रमेय के रूप में दिया गया है।

प्रमेय 2 किसी भी धनात्मक पूर्णांक $n$ के लिए,

$ \lim\limits_{x \to a} \frac{x^{n}-a^{n}}{x-a}=n a^{n-1} $

टिप्पणी उपरोक्त प्रमेय में सीमा के लिए व्यंजक तब भी सत्य है जब $n$ कोई परिमेय संख्या हो और $a$ धनात्मक हो।

प्रमाण $(x^{n}-a^{n})$ को $(x-a)$ से विभाजित करने पर, हम देखते हैं कि

$ x^{n}-a^{n}=(x-a)(x^{n-1}+x^{n-2} a+x^{n-3} a^{2}+\ldots+x a^{n-2}+a^{n-1}) $

$ \begin{aligned} \text{इस प्रकार, }\quad \lim\limits_{x \to a} \frac{x^{n}-a^{n}}{x-a}& =\lim\limits_{x \to a}(x^{n-1}+x^{n-2} a+x^{n-3} a^{2}+\ldots+x a^{n-2}+a^{n-1}) \\ & =a^{n-1}+a a^{n-2}+\ldots+a^{n-2}(a)+a^{n-1} \\ & =a^{n-1}+a^{n-1}+\ldots+a^{n-1}+a^{n-1}(n \text{ पद }) \\ & =n a^{n-1} \end{aligned} $

उदाहरण 3 मूल्यांकन कीजिए:

(i) $\lim\limits_{x \to 1} \frac{x^{15}-1}{x^{10}-1}$

(ii) $\lim\limits_{x \to 0} \frac{\sqrt{1+x}-1}{x}$

हल (i) हमारे पास

$ \begin{aligned} \lim\limits_{x \to 1} \frac{x^{15}-1}{x^{10}-1} & =\lim\limits_{x \to 1}[\frac{x^{15}-1}{x-1} \div \frac{x^{10}-1}{x-1}] \\ & =\lim\limits_{x \to 1}[\frac{x^{15}-1}{x-1}] \div \lim\limits_{x \to 1}[\frac{x^{10}-1}{x-1}] \\ & =15(1)^{14} \div 10(1)^{9} \text{ (उपरोक्त प्रमेय द्वारा) } \\ & =15 \div 10=\frac{3}{2} \end{aligned} $

(ii) मान लीजिए $y=1+x$, ताकि $x \to 0$ के साथ $y \to 1$.

$ \begin{aligned} \text{तब} \quad \lim\limits_{x \to 0} \frac{\sqrt{1+x}-1}{x}& =\lim\limits_{y \to 1} \frac{\sqrt{y}-1}{y-1} \\ & =\lim\limits_{y \to 1} \frac{y^{\frac{1}{2}}-1^{\frac{1}{2}}}{y-1} \\ & =\frac{1}{2}(1)^{\frac{1}{2}-1}(\text{उपरोक्त टिप्पणी द्वारा})=\frac{1}{2} \end{aligned} $

12.4 त्रिकोणमितीय फलनों की सीमाएँ

फलनों के बारे में निम्नलिखित तथ्य (प्रमेयों के रूप में कहे गए) सामान्य रूप से कुछ त्रिकोणमितीय फलनों की सीमाएँ निकालने में उपयोगी सिद्ध होते हैं।

प्रमेय 3 मान लीजिए (f) और (g) दो वास्तविक मान फलन हैं जिनका एक ही डोमेन है, इस प्रकार कि (f(x) \leq g(x)) सभी (x) के लिए जो परिभाषा के डोमेन में हैं। किसी (a) के लिए, यदि दोनों (\lim\limits_{x \to a} f(x)) और (\lim\limits_{x \to a} g(x)) अस्तित्व में हैं, तो (\lim\limits_{x \to a} f(x) \leq \lim\limits_{x \to a} g(x))। इसे आकृति 12.8 में दर्शाया गया है।

आकृति 12.8

प्रमेय 4 (सैंडविच प्रमेय) मान लीजिए (f), (g) और (h) वास्तविक फलन हैं इस प्रकार कि (f(x) \leq g(x) \leq h(x)) सभी (x) के लिए जो उनके सामान्य परिभाषा के डोमेन में हैं। किसी वास्तविक संख्या (a) के लिए, यदि (\lim\limits_{x \to a} f(x)=l=\lim\limits_{x \to a} h(x)), तो (\lim\limits_{x \to a} g(x)=l)। इसे आकृति 12.9 में दर्शाया गया है।

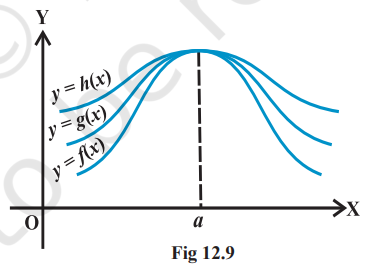
आकृति 12.9

नीचे त्रिकोणमितीय फलनों से संबंधित निम्नलिखित महत्वपूर्ण असमता का एक सुंदर ज्यामितीय प्रमाण दिया गया है।

$$ \cos x<\frac{\sin x}{x}<1 \quad \text{ for } 0<|x|<\frac{\pi}{2} \quad \quad \quad \quad \quad ({}^*) $$

प्रमाण हम जानते हैं कि (\sin (-x)=-\sin x) और (\cos (-x)=\cos x)। इसलिए, यह असमता को (0<x<\frac{\pi}{2}) के लिए सिद्ध करना पर्याप्त है।

चित्र 12.10 में, $O$ इकाई वृत्त का केंद्र है इस प्रकार कि कोण AOC $x$ रेडियन है और $0<x<\frac{\pi}{2}$। रेखाखंड BA और $CD$, $OA$ पर लंब हैं। आगे, $AC$ को मिलाइए। तब

चित्र 12.10

$\triangle OAC$ का क्षेत्रफल < सैक्टर OAC का क्षेत्रफल < $\triangle OAB$ का क्षेत्रफल।

अर्थात्, $\quad \frac{1}{2} OA . CD<\frac{x}{2 \pi} . \pi .(OA)^{2}<\frac{1}{2} OA . AB$।

अर्थात्, $\quad CD<x . OA<AB$।

$\triangle OCD$ से,

$ \sin x=\frac{CD}{OA}(\text{ चूँकि } OC=OA) \text{ और इसलिए } CD=OA \sin x \text{। साथ ही } \tan x=\frac{AB}{OA} \text{ और } $

इसलिए $\quad AB=OA \cdot \tan x$। इस प्रकार

$ \text{ OA } \sin x<\text{ OA. } x<\text{ OA. } \tan x . $

चूँकि OA की लंबाई धनात्मक है, हमें प्राप्त होता है

$ \sin x<x<\tan x \text{। } $

चूँकि $0<x<\frac{\pi}{2}, \sin x$ धनात्मक है और इस प्रकार $\sin x$ से पूरे को भाग देने पर, हमें प्राप्त होता है

$1<\frac{x}{\sin x}<\frac{1}{\cos x} . \quad$ पूरे में व्युत्क्रम लेने पर, हमें प्राप्त होता है

$ \cos x<\frac{\sin x}{x}<1 $

जो प्रमाण को पूरा करता है।

प्रमेय 5 निम्नलिखित दो महत्वपूर्ण सीमाएँ हैं।

(i) $\lim\limits_{x \to 0} \frac{\sin x}{x}=1$।

(ii) $\lim\limits_{x \to 0} \frac{1-\cos x}{x}=0$।

प्रमाण (i) असमता (*) कहती है कि फलन $\frac{\sin x}{x}$ फलन $\cos x$ और नियत फलन जिसका मान 1 है, के बीच दबा हुआ है।

आगे, चूँकि $\lim\limits_{x \to 0} \cos x=1$, हम देखते हैं कि प्रमेय के (i) का प्रमाण सैंडविच प्रमेय द्वारा पूर्ण हो गया है।

(ii) को सिद्ध करने के लिए, हम त्रिकोणमितीय सर्वसमिका $1-\cos x=2 \sin ^{2}(\frac{x}{2})$ को स्मरण करते हैं। तब

$ \begin{aligned} \lim\limits_{x \to 0} \frac{1-\cos x}{x} & =\lim\limits_{x \to 0} \frac{2 \sin ^{2}(\frac{x}{2})}{x}=\lim\limits_{x \to 0} \frac{\sin (\frac{x}{2})}{\frac{x}{2}} \cdot \sin (\frac{x}{2}) \ & =\lim\limits_{x \to 0} \frac{\sin (\frac{x}{2})}{\frac{x}{2}} \cdot \lim\limits_{x \to 0} \sin (\frac{x}{2})=1.0=0 \end{aligned} $

ध्यान दें कि हमने निहित रूप से यह तथ्य प्रयोग किया है कि $x \to 0$ का अर्थ $\frac{x}{2} \to 0$ के बराबर है। इसे $y=\frac{x}{2}$ रखकर औचित्य दिया जा सकता है।

उदाहरण 4 मूल्यांकन कीजिए:

(i) $\lim\limits_{x \to 0} \frac{\sin 4 x}{\sin 2 x}$

(ii) $\lim\limits_{x \to 0} \frac{\tan x}{x}$

हल $ \begin{aligned} \text{(i)} \quad \lim\limits_{x \to 0} \frac{\sin 4 x}{\sin 2 x}& =\lim\limits_{x \to 0}[\frac{\sin 4 x}{4 x} \cdot \frac{2 x}{\sin 2 x} \cdot 2] \ & =2 \cdot \lim\limits_{x \to 0}[\frac{\sin 4 x}{4 x}] \div[\frac{\sin 2 x}{2 x}] \ & =2 \cdot \lim\limits_{4 x \to 0}[\frac{\sin 4 x}{4 x}] \div \lim\limits_{2 x \to 0}[\frac{\sin 2 x}{2 x}] \ & =2 \cdot 1 \cdot 1=2(\text{ चूँकि } x \to 0,4 x \to 0 \text{ और } 2 x \to 0) \end{aligned} $

(ii) हमारे पास है $\lim\limits_{x \to 0} \frac{\tan x}{x}=\lim\limits_{x \to 0} \frac{\sin x}{x \cos x}=\lim\limits_{x \to 0} \frac{\sin x}{x} \cdot \lim\limits_{x \to 0} \frac{1}{\cos x}=1.1=1$

सीमाओं का मूल्यांकन करते समय ध्यान में रखी जाने वाली एक सामान्य नियम निम्नलिखित है। मान लीजिए, यह दिया गया है कि सीमा $\lim\limits_{x \to a} \frac{f(x)}{g(x)}$ अस्तित्व में है और हम इसका मूल्यांकन करना चाहते हैं। सबसे पहले हम $f(a)$ और $g(a)$ का मान जांचते हैं। यदि दोनों 0 हैं, तो हम देखते हैं कि क्या हम वह कारक प्राप्त कर सकते हैं जिससे पद लुप्त हो रहे हैं, अर्थात् हम देखते हैं कि क्या हम $f(x)=f_1(x) f_2(x)$ इस प्रकार लिख सकते हैं कि $f_1(a)=0$ और $f_2(a) \neq 0$। इसी प्रकार, हम $g(x)=g_1(x) g_2(x)$ लिखते हैं, जहाँ $g_1(a)=0$ और $g_2(a) \neq 0$। $f(x)$ और $g(x)$ से सामान्य कारकों को रद्द करें (यदि संभव हो) और लिखें

$\quad \quad \quad \quad\quad \quad \quad \frac{f(x)}{g(x)}=\frac{p(x)}{q(x)}, \text{ जहाँ } q(x) \neq 0 $

तब $\quad \quad \quad \quad \quad \lim\limits_{x \to a} \frac{f(x)}{g(x)}=\frac{p(a)}{q(a)}$.

12.5 अवकलज

हमने अनुच्छेद 13.2 में देखा है कि किसी वस्तु की स्थिति को विभिन्न समय अंतरालों पर जानकर यह पता लगाना संभव है कि वस्तु की स्थिति किस दर से बदल रही है। विभिन्न समय क्षणों पर किसी निश्चित मापदंड को जानना और यह जानने का प्रयास करना कि वह किस दर से बदल रहा है, बहुत सामान्य रुचि का विषय है। ऐसी कई वास्तविक जीवन की स्थितियाँ हैं जहाँ इस प्रक्रिया को अंजाम देने की आवश्यकता होती है। उदाहरण के लिए, एक जलाशय के रखरखाव करने वाले लोगों को यह जानना होता है कि जलाशय कब overflow करेगा, यह जानते हुए कि समय के विभिन्न क्षणों पर पानी की गहराई क्या है; रॉकेट वैज्ञानिकों को यह गणना करनी होती है कि उपग्रह को रॉकेट से किस सटीक वेग से छोड़ा जाए, यह जानते हुए कि विभिन्न समयों पर रॉकेट की ऊँचाई क्या है; वित्तीय संस्थाओं को किसी विशेष स्टॉक के मूल्य में होने वाले परिवर्तनों की भविष्यवाणी करनी होती है, यह जानते हुए कि उसका वर्तमान मूल्य क्या है। इन और ऐसे ही कई मामलों में यह जानना वांछनीय होता है कि कोई विशेष मापदंड किसी अन्य मापदंड के सापेक्ष किस प्रकार बदल रहा है। इसका मूल बिंदु है फलन का व्युत्पन्न उसके परिभाषा क्षेत्र के किसी दिए गए बिंदु पर।

परिभाषा 1 मान लीजिए $f$ एक वास्तविक मान वाला फलन है और a उसके परिभाषा क्षेत्र का एक बिंदु है। $f$ का a पर व्युत्पन्न इस प्रकार परिभाषित है

$ \lim\limits_{h \to 0} \frac{f(a+h)-f(a)}{h} $

बशर्ते यह सीमा अस्तित्व में हो। $f(x)$ का a पर व्युत्पन्न $f^{\prime}(a)$ द्वारा दर्शाया जाता है।

ध्यान दीजिए कि $f^{\prime}(a)$, a पर $f(x)$ में x के सापेक्ष होने वाले परिवर्तन को मात्रात्मक रूप से व्यक्त करता है।

उदाहरण 5 फलन (f(x)=3 x) का (x=2) पर अवकलज ज्ञात कीजिए।

हल हमारे पास

$ \begin{aligned} f^{\prime}(2) & =\lim\limits_{h \to 0} \frac{f(2+h)-f(2)}{h}=\lim\limits_{h \to 0} \frac{3(2+h)-3(2)}{h} \ & =\lim\limits_{h \to 0} \frac{6+3 h-6}{h}=\lim\limits_{h \to 0} \frac{3 h}{h}=\lim\limits_{h \to 0} 3=3 . \end{aligned} $

फलन (3 x) का (x=2) पर अवकलज 3 है।

उदाहरण 6 फलन (f(x)=2 x^{2}+3 x-5) का (x=-1) पर अवकलज ज्ञात कीजिए। यह भी सिद्ध कीजिए कि (f^{\prime}(0)+3 f^{\prime}(-1)=0).

हल हम पहले (f(x)) का (x=-1) और (x=0) पर अवकलज ज्ञात करते हैं। हमारे पास

$ \begin{array}{lll} &f^{\prime}(-1) & =\lim\limits_{h \rightarrow 0} \frac{f(-1+h)-f(-1)}{h} \\ & {}& =\lim\limits_{h \rightarrow 0} \frac{[2(-1+h)^{2}+3(-1+h)-5]-[2(-1)^{2}+3(-1)-5]}{h} \\ & {}& =\lim\limits_{h \rightarrow 0} \frac{2 h^{2}-h}{h}=\lim\limits_{h \rightarrow 0}(2 h-1)=2(0)-1=-1 \\ \text{और } & f^{\prime}(0) & =\lim\limits_{h \rightarrow 0} \frac{f(0+h)-f(0)}{h} \\ & {}& =\lim\limits_{h \rightarrow 0} \frac{[2(0+h)^{2}+3(0+h)-5]-[2(0)^{2}+3(0)-5]}{h} \\ & {}& =\lim\limits_{h \rightarrow 0} \frac{2 h^{2}+3 h}{h}=\lim\limits_{h \rightarrow 0}(2 h+3)=2(0)+3=3 \end{array} $

स्पष्टतः (\quad \quad \quad \quad f^{\prime}(0)+3 f^{\prime}(-1)=0 )

टिप्पणी इस चरण पर ध्यान दें कि किसी बिंदु पर अवकलज का मूल्यांकन विभिन्न नियमों का प्रभावी उपयोग करता है, जिनके अधीन सीमाएँ होती हैं। निम्नलिखित इसे दर्शाता है।

उदाहरण 7 $x=0$ पर $\sin x$ का अवकलज ज्ञात कीजिए।

हल मान लीजिए $f(x)=\sin x$। तब

$ \begin{aligned} f^{\prime}(0) & =\lim\limits_{h \to 0} \frac{f(0+h)-f(0)}{h} \ & =\lim\limits_{h \to 0} \frac{\sin (0+h)-\sin (0)}{h}=\lim\limits_{h \to 0} \frac{\sin h}{h}=1 \end{aligned} $

उदाहरण 8 $f(x)=3$ का अवकलज $x=0$ और $x=3$ पर ज्ञात कीजिए।

हल चूँकि अवकलज फलन में परिवर्तन को मापता है, सहज रूप से यह स्पष्ट है कि नियत फलन का अवकलज प्रत्येक बिंदु पर शून्य होना चाहिए। यह वास्तव में निम्नलिखित गणना द्वारा समर्थित है।

$$ f^{\prime}(0)=\lim\limits_{h \to 0} \frac{f(0+h)-f(0)}{h}=\lim\limits_{h \to 0} \frac{3-3}{h}=\lim\limits_{h \to 0} \frac{0}{h}=0 . $$

इसी प्रकार $\quad f^{\prime}(3)=\lim\limits_{h \to 0} \frac{f(3+h)-f(3)}{h}=\lim\limits_{h \to 0} \frac{3-3}{h}=0$।

अब हम किसी फलन के किसी बिंदु पर अवकलज की एक ज्यामितीय व्याख्या प्रस्तुत करते हैं। मान लीजिए $y=f(x)$ एक फलन है और मान लीजिए $P=(a, f(a))$ और $Q=(a+h, f(a+h)$ इस फलन के आलेख पर एक-दूसरे के निकट दो बिंदु हैं। आकृति 12.11 अब स्वतः स्पष्ट है।

आकृति 12.11

हम जानते हैं कि $f^{\prime}(a)=\lim\limits_{h \to 0} \frac{f(a+h)-f(a)}{h}$

त्रिभुज $PQR$ से यह स्पष्ट है कि जिस अनुपात की सीमा हम ले रहे हैं, वह ठीक-ठीक $\tan (QPR)$ के बराबर है जो जीवा $PQ$ की ढाल है। सीमाबद्ध प्रक्रिया में, जैसे-जैसे $h$ शून्य की ओर जाता है, बिंदु $Q$ बिंदु $P$ की ओर जाता है और हमें मिलता है

$ \lim\limits_{h \to 0} \frac{f(a+h)-f(a)}{h}=\lim\limits_{Q \to P} \frac{QR}{PR} $

यह तथ्य के समतुल्य है कि जीवा $PQ$ वक्र $y=f(x)$ के बिंदु $P$ पर स्पर्शरेखा की ओर जाती है। इस प्रकार सीमा स्पर्शरेखा की ढाल के बराबर निकलती है। इसलिए

$ f^{\prime}(a)=\tan \psi $

किसी दी गई फलन $f$ के लिए हम प्रत्येक बिंदु पर अवकलज प्राप्त कर सकते हैं। यदि अवकलज प्रत्येक बिंदु पर अस्तित्व रखता है, तो यह एक नई फलन को परिभाषित करता है जिसे $f$ का अवकलज कहा जाता है। औपचारिक रूप से, हम फलन के अवकलज को इस प्रकार परिभाषित करते हैं।

परिभाषा 2 मान लीजिए $f$ एक वास्तविक मान वाला फलन है, फलन जो

$ \lim\limits_{h \to 0} \frac{f(x+h)-f(x)}{h} $

जहाँ भी सीमा अस्तित्व रखती है, को $x$ पर $f$ का अवकलज कहा जाता है और इसे $f^{\prime}(x)$ द्वारा निरूपित किया जाता है। अवकलज की यह परिभाषा को अवकलज का प्रथम सिद्धांत भी कहा जाता है।

इस प्रकार $ \quad \quad \quad f^{\prime}(x)=\lim\limits_{h \to 0} \frac{f(x+h)-f(x)}{h} $

स्पष्ट रूप से $f^{\prime}(x)$ का परिभाषा क्षेत्र वहाँ है जहाँ उपरोक्त सीमा विद्यमान है। किसी फलन के अवकलज के लिए विभिन्न संकेतन हैं। कभी-कभी $f^{\prime}(x)$ को $\frac{d}{d x}(f(x))$ द्वारा दर्शाया जाता है या यदि $y=f(x)$ है, तो इसे $\frac{d y}{d x}$ द्वारा दर्शाया जाता है। इसे $f(x)$ या $y$ का $x$ के सापेक्ष अवकलज कहा जाता है। इसे $D(f(x))$ द्वारा भी दर्शाया जाता है। इसके अतिरिक्त, $f$ का $x=a$ पर अवकलज $.\frac{d}{dx} f(x)| _ {a} $ या $.\frac{df}{dx}| _ {a} $ या $(\frac{d f}{d x}) _ {x=a}$ द्वारा भी दर्शाया जाता है।

उदाहरण 9 $f(x)=10 x$ का अवकलज ज्ञात कीजिए।

हल चूँकि $f^{\prime}(x)=\lim\limits_{h \to 0} \frac{f(x+h)-f(x)}{h}$

$ \begin{aligned} & =\lim\limits_{h \to 0} \frac{10(x+h)-10(x)}{h} \ & =\lim\limits_{h \to 0} \frac{10 h}{h}=\lim\limits_{h \to 0}(10)=10 . \end{aligned} $

उदाहरण 10 $f(x)=x^{2}$ का अवकलज ज्ञात कीजिए।

हल हमारे पास, $f^{\prime}(x)=\lim\limits_{h \to 0} \frac{f(x+h)-f(x)}{h}$

$ =\lim\limits_{h \to 0} \frac{(x+h)^{2}-(x)^{2}}{h}=\lim\limits_{h \to 0}(h+2 x)=2 x $

उदाहरण 11 नियत वास्तविक संख्या $a$ के लिए नियत फलन $f(x)=a$ का अवकलज ज्ञात कीजिए।

हल हमारे पास, $f^{\prime}(x)=\lim\limits_{h \to 0} \frac{f(x+h)-f(x)}{h}$

$ =\lim\limits_{h \to 0} \frac{a-a}{h}=\lim\limits_{h \to 0} \frac{0}{h}=0 \text{ क्योंकि } h \neq 0 $

उदाहरण 12 $f(x)=\frac{1}{x}$ का अवकलज ज्ञात कीजिए।

हल हमारे पास $f^{\prime}(x)=\lim\limits_{h \to 0} \frac{f(x+h)-f(x)}{h}$

$ \begin{aligned} & =\lim\limits_{h \to 0} \frac{\frac{1}{(x+h)}-\frac{1}{x}}{h} \\ & =\lim\limits_{h \to 0} \frac{1}{h}[\frac{x-(x+h)}{x(x+h)}] \\ & =\lim\limits_{h \to 0} \frac{1}{h}[\frac{-h}{x(x+h)}] \quad=\lim\limits_{h \to 0} \frac{-1}{x(x+h)}=-\frac{1}{x^{2}} \end{aligned} $

12.5.1 फलनों के अवकलज का बीजगणित

चूँकि अवकलज की परिभाषा स्वयं सीधे-सीधे सीमाओं से जुड़ी है, हम अपेक्षा करते हैं कि अवकलजों के नियम सीमाओं के नियमों से काफी मिलते-जुलते होंगे। हम उन्हें निम्नलिखित प्रमेय में संकलित करते हैं।

प्रमेय 5 मान लीजिए $f$ और $g$ दो फलन इस प्रकार हैं कि उनके अवकलज एक उभयनिष्ठ प्रांत में परिभाषित हैं। तब

(i) दो फलनों के योग का अवकलज, फलनों के अवकलजों के योग के बराबर होता है।

$$ \frac{d}{d x}[f(x)+g(x)]=\frac{d}{d x} f(x)+\frac{d}{d x} g(x) . $$

(ii) दो फलनों के अंतर का अवकलज, फलनों के अवकलजों के अंतर के बराबर होता है।

$$ \frac{d}{d x}[f(x)-g(x)]=\frac{d}{d x} f(x)-\frac{d}{d x} g(x) $$

(iii) दो फलनों के गुणनफल का अवकलज निम्नलिखित गुणनफल नियम द्वारा दिया जाता है।

$$ \frac{d}{d x}[f(x) \cdot g(x)]=\frac{d}{d x} f(x) \cdot g(x)+f(x) \cdot \frac{d}{d x} g(x) $$

(iv) दो फलनों के भाग का अवकलज निम्नलिखित भाग नियम द्वारा दिया जाता है (जब भी हर शून्येतर हो)।

$$ \frac{d}{d x}(\frac{f(x)}{g(x)})=\frac{\frac{d}{d x} f(x) \cdot g(x)-f(x) \frac{d}{d x} g(x)}{(g(x))^{2}} $$

इनके प्रमाण मूलतः सीमाओं के समान प्रमेय से प्राप्त होते हैं। हम इन्हें यहाँ प्रमाणित नहीं करेंगे। जैसे सीमाओं के मामले में, यह प्रमेय हमें बताता है कि विशेष प्रकार के फलनों के अवकलज कैसे निकाले जाएँ। प्रमेय के अंतिम दो कथनों को निम्नलिखित ढंग से पुनः व्यक्त किया जा सकता है जो उन्हें आसानी से याद रखने में सहायक होता है:

मान लीजिए $u=f(x)$ और $v=g(x)$। तब

$ (u v)^{\prime}=u^{\prime} v+u v^{\prime} $

इसे फलनों के गुणनफल के अवकलन के लिए लाइबनिट्ज़ नियम या गुणनफल नियम कहा जाता है। इसी प्रकार, भागफल नियम है

$ (\frac{u}{v})^{\prime}=\frac{u^{\prime} v-u v^{\prime}}{v^{2}} $

अब, आइए कुछ मानक फलनों के अवकलजों पर विचार करें।

यह देखना आसान है कि फलन $f(x)=x$ का अवकलज नियत फलन 1 है। ऐसा इसलिए है क्योंकि $f^{\prime}(x)=\lim\limits_{h \to 0} \frac{f(x+h)-f(x)}{h}=\lim\limits_{h \to 0} \frac{x+h-x}{h}$

$ =\lim\limits_{h \to 0} 1=1 \text{. } $

हम इसका और ऊपर दिए गए प्रमेय का उपयोग करके $f(x)=10 x=x+\ldots .+x$ (दस पदों) का अवकलज निकालते हैं। उपरोक्त प्रमेय के $(i)$ से

$ \begin{aligned} \frac{d f(x)}{d x} & =\frac{d}{d x}(x+\ldots+x) \quad(\text{ दस पद }) \\ & =\frac{d}{d x} x+\ldots+\frac{d}{d x} x \quad(\text{ दस पद }) \\ & =1+\ldots+1 \quad(\text{ दस पद })=10 \end{aligned} $

हम ध्यान देते हैं कि यह सीमा उत्पाद नियम का उपयोग करके भी मूल्यांकन की जा सकती है। लिखें $f(x)=10 x=u v$, जहाँ $u$ एक नियत फलन है जो हर जगह मान 10 लेता है और $v(x)=x$। यहाँ, $f(x)=10 x=u v$ हम जानते हैं कि $u$ का अवकलज 0 के बराबर है। साथ ही $v(x)=x$ का अवकलज 1 के बराबर है। इस प्रकार उत्पाद नियम से हम पाते हैं

$ f^{\prime}(x)=(10 x)^{\prime}=(u v)^{\prime}=u^{\prime} v+u v^{\prime}=0 \cdot x+10.1=10 $

इसी तरह की पंक्तियों पर $f(x)=x^{2}$ का अवकलज मूल्यांकन किया जा सकता है। हमारे पास $f(x)=x^{2}=x . x$ है और इसलिए

$$ \begin{aligned} \frac{d f}{d x} & =\frac{d}{d x}(x \cdot x)=\frac{d}{d x}(x) \cdot x+x \cdot \frac{d}{d x}(x) \\ & =1 \cdot x+x \cdot 1=2 x . \end{aligned} $$

अधिक सामान्य रूप से, हमारे पास निम्नलिखित प्रमेय है।

प्रमेय 6 $f(x)=x^{n}$ का अवकलज $n x^{n-1}$ है किसी भी धनात्मक पूर्णांक $n$ के लिए।

प्रमाण अवकलज फलन की परिभाषा से, हमारे पास

$ f^{\prime}(x)=\lim\limits_{h \to 0} \frac{f(x+h)-f(x)}{h}=\lim\limits_{h \to 0} \frac{(x+h)^{n}-x^{n}}{h} . $

द्विपद प्रमेय बताती है कि $(x+h)^{n}=({ }^{n} C_0) x^{n}+({ }^{n} C_1) x^{n-1} h+\ldots+({ }^{n} C_n) h^{n}$ और इसलिए $(x+h)^{n}-x^{n}=h(n x^{n-1}+\ldots+h^{n-1})$ है। इस प्रकार

$ \begin{aligned} \frac{d f(x)}{d x} & =\lim\limits_{h \to 0} \frac{(x+h)^{n}-x^{n}}{h} \\ & =\lim\limits_{h \to 0} \frac{h(n x^{n-1}+\ldots .+h^{n-1})}{h} \\ & =\lim\limits_{h \to 0}(n x^{n-1}+\ldots+h^{n-1})=n x^{n-1} . \end{aligned} $

वैकल्पिक रूप से, हम इसे $n$ पर आगमन और गुणन नियम के द्वारा इस प्रकार भी सिद्ध कर सकते हैं। परिणाम $n=1$ के लिए सत्य है, जिसे पहले सिद्ध किया जा चुका है। हमारे पास

$ \begin{aligned} \frac{d}{d x}(x^{n}) & =\frac{d}{d x}(x \cdot x^{n-1}) \ & =\frac{d}{d x}(x) \cdot(x^{n-1})+x \cdot \frac{d}{d x}(x^{n-1}) \text{ (गुणन नियम द्वारा) } \ & =1 \cdot x^{n-1}+x \cdot((n-1) x^{n-2}) \text{ (आगमन पूर्वधारणा द्वारा) } \ & =x^{n-1}+(n-1) x^{n-1}=n x^{n-1} . \end{aligned} $

टिप्पणी उपरोक्त प्रमेय $x$ की सभी घातों के लिए सत्य है, अर्थात् $n$ कोई भी वास्तविक संख्या हो सकती है (परंतु हम यहाँ इसे सिद्ध नहीं करेंगे)।

12.5.2 बहुपद और त्रिकोणमितीय फलनों का अवकलज

हम निम्नलिखित प्रमेय से प्रारंभ करते हैं जो हमें बहुपद फलन के अवकलज के बारे में बताती है।

प्रमेय 7 मान लीजिए $f(x)=a_n x^{n}+a_{n-1} x^{n-1}+\ldots .+a_1 x+a_0$ एक बहुपद फलन है, जहाँ $a_i$ सभी वास्तविक संख्याएँ हैं और $a_n \neq 0$। तब, अवकलज फलन दिया गया है

$ \frac{d f(x)}{d x}=n a_n x^{n-1}+(n-1) a_{n-1} x^{n-2}+\ldots+2 a_2 x+a_1 $

इस प्रमेय का प्रमाण प्रमेय 5 के भाग (i) और प्रमेय 6 को एक साथ रखने मात्र से है।

उदाहरण 13 $6 x^{100}-x^{55}+x$ का अवकलज ज्ञात कीजिए।

हल उपरोक्त प्रमेय का प्रत्यक्ष प्रयोग बताता है कि उपरोक्त फलन का अवकलज $600 x^{99}-55 x^{54}+1$ है।

उदाहरण 14 $f(x)=1+x+x^{2}+x^{3}+\ldots+x^{50}$ का अवकलज $x=1$ पर ज्ञात कीजिए।

हल उपरोक्त प्रमेय 6 का सीधा प्रयोग बताता है कि उपरोक्त फलन का अवकलन $1+2 x+3 x^{2}+\ldots+50 x^{49}$ है। $x=1$ पर इस फलन का मान $1+2(1)+3(1)^{2}+\ldots+50(1)^{49}=1+2+3+\ldots+50=\frac{(50)(51)}{2}=1275$ है।

उदाहरण 15 $f(x)=\frac{x+1}{x}$ का अवकलन ज्ञात कीजिए।

हल स्पष्ट है कि यह फलन $x=0$ को छोड़कर हर जगह परिभाषित है। हम भागफल नियम का प्रयोग करते हैं जहाँ $u=x+1$ और $v=x$ है। इसलिए $u^{\prime}=1$ और $v^{\prime}=1$ है। इसलिए

$ \frac{d f(x)}{d x}=\frac{d}{d x}(\frac{x+1}{x})=\frac{d}{d x}(\frac{u}{v})=\frac{u^{\prime} v-u v^{\prime}}{v^{2}}=\frac{1(x)-(x+1) 1}{x^{2}}=-\frac{1}{x^{2}} $

उदाहरण 16 $\sin x$ का अवकलन ज्ञात कीजिए।

हल मान लीजिए $f(x)=\sin x$ है। तब

$ \begin{aligned} \frac{d f(x)}{d x} & =\lim\limits_{h \to 0} \frac{f(x+h)-f(x)}{h}=\lim\limits_{h \to 0} \frac{\sin (x+h)-\sin (x)}{h} \ & =\lim\limits_{h \to 0} \frac{2 \cos (\frac{2 x+h}{2}) \sin (\frac{h}{2})}{h} \text{ (sin A - sin B के सूत्र का प्रयोग करते हुए) } \ & =\lim\limits_{h \to 0} \cos (x+\frac{h}{2}) \cdot \lim\limits_{h \to 0} \frac{\sin \frac{h}{2}}{\frac{h}{2}}=\cos x \cdot 1=\cos x . \end{aligned} $

उदाहरण 17 $\tan x$ का अवकलन ज्ञात कीजिए।

हल मान लीजिए $f(x)=\tan x$ है। तब

$ \begin{aligned} \frac{d f(x)}{d x} & =\lim\limits_{h \to 0} \frac{f(x+h)-f(x)}{h}=\lim\limits_{h \to 0} \frac{\tan (x+h)-\tan (x)}{h} \ & =\lim\limits_{h \to 0} \frac{1}{h}\left[\frac{\sin (x+h)}{\cos (x+h)}-\frac{\sin x}{\cos x}\right] \ & =\lim\limits_{h \to 0}\left[\frac{\sin (x+h) \cos x-\cos (x+h) \sin x}{h \cos (x+h) \cos x}\right] \ & .=\lim\limits_{h \to 0} \frac{\sin (x+h-x)}{h \cos (x+h) \cos x} \text{ (using formula for sin }(A+B)) \ & =\lim\limits_{h \to 0} \frac{\sin h}{h} \cdot \lim\limits_{h \to 0} \frac{1}{\cos (x+h) \cos x} \ & =1 \cdot \frac{1}{\cos ^{2} x}=\sec ^{2} x . \end{aligned} $

उदाहरण 18 $f(x)=\sin ^{2} x$ का अवकलज ज्ञात कीजिए।

हल हम इसे मूल्यांकित करने के लिए लाइबनिट्ज़ गुणनफल नियम का उपयोग करते हैं।

$ \begin{aligned} \frac{d f(x)}{d x} & =\frac{d}{d x}(\sin x \sin x) \ & =(\sin x)^{\prime} \sin x+\sin x(\sin x)^{\prime} \ & =(\cos x) \sin x+\sin x(\cos x) \ & =2 \sin x \cos x=\sin 2 x . \end{aligned} $

विविध उदाहरण

उदाहरण 19 प्रथम सिद्धांत से $f$ का अवकलज ज्ञात कीजिए, जहाँ $f$ निम्नलिखित रूप में दिया गया है

(i) $f(x)=\frac{2 x+3}{x-2}$

(ii) $f(x)=x+\frac{1}{x}$

हल (i) ध्यान दें कि फलन $x=2$ पर परिभाषित नहीं है। लेकिन, हमारे पास

$ \begin{aligned} f^{\prime}(x)&=\lim\limits_{h \to 0} \frac{f(x+h)-f(x)}{h}=\lim\limits_{h \to 0} \frac{\frac{2(x+h)+3}{x+h-2}-\frac{2 x+3}{x-2}}{h} \\ \\ & =\lim\limits_{h \to 0} \frac{(2 x+2 h+3)(x-2)-(2 x+3)(x+h-2)}{h(x-2)(x+h-2)} \\ \\ & =\lim\limits_{h \to 0} \frac{(2 x+3)(x-2)+2 h(x-2)-(2 x+3)(x-2)-h(2 x+3)}{h(x-2)(x+h-2)} \\ \\ & =\lim\limits_{h \to 0} \frac{-7}{(x-2)(x+h-2)}=-\frac{7}{(x-2)^{2}} \end{aligned} $

फिर से ध्यान दें कि फलन $f^{\prime}$ भी $x=2$ पर परिभाषित नहीं है। (ii) फलन $x=0$ पर परिभाषित नहीं है। पर, हमारे पास है

$ \begin{aligned} f^{\prime}(x) & =\lim\limits_{h \to 0} \frac{f(x+h)-f(x)}{h}=\lim\limits_{h \to 0} \frac{(x+h+\frac{1}{x+h})-(x+\frac{1}{x})}{h} \\ \\ & =\lim\limits_{h \to 0} \frac{1}{h}\left[h+\frac{1}{x+h}-\frac{1}{x}\right] \\ \\ & =\lim\limits_{h \to 0} \frac{1}{h}\left[h+\frac{x-x-h}{x(x+h)}\right]=\lim\limits_{h \to 0} \frac{1}{h}\left[h\left(1-\frac{1}{x(x+h)}\right)\right] \\ \\ & =\lim\limits_{h \to 0}\left[1-\frac{1}{x(x+h)}\right]=1-\frac{1}{x^{2}} \end{aligned} $

फिर से ध्यान दें कि फलन $f^{\prime}$ का $x=0$ पर अस्तित्व नहीं है।

उदाहरण 20 प्रथम सिद्धांत से $f(x)$ का अवकलज ज्ञात कीजिए, जहाँ $f(x)$ है (i) $\sin x+\cos x$ (ii) $x \sin x$

हल (i) हमारे पास $f^{\prime}(x)=\frac{f(x+h)-f(x)}{h}$

$ \begin{aligned} & =\lim\limits_{h \to 0} \frac{\sin (x+h)+\cos (x+h)-\sin x-\cos x}{h} \\ & =\lim\limits_{h \to 0} \frac{\sin x \cos h+\cos x \sin h+\cos x \cos h-\sin x \sin h-\sin x-\cos x}{h} \end{aligned} $

$ \begin{aligned} & =\lim\limits_{h \to 0} \frac{\sin h(\cos x-\sin x)+\sin x(\cos h-1)+\cos x(\cos h-1)}{h} \\ & =\lim\limits_{h \to 0} \frac{\sin h}{h}(\cos x-\sin x)+\lim\limits_{h \to 0} \sin x \frac{(\cos h-1)}{h}+\lim\limits_{h \to 0} \cos x \frac{(\cos h-1)}{h} \\ & =\cos x-\sin x \end{aligned} $

(ii) $\quad f^{\prime}(x)=\lim\limits_{h \to 0} \frac{f(x+h)-f(x)}{h}=\lim\limits_{h \to 0} \frac{(x+h) \sin (x+h)-x \sin x}{h}$

$ =\lim\limits_{h \to 0} \frac{(x+h)(\sin x \cos h+\sin h \cos x)-x \sin x}{h} $

$ \begin{aligned} & \quad=\lim\limits_{h \to 0} \frac{x \sin x(\cos h-1)+x \cos x \sin h+h(\sin x \cos h+\sin h \cos x)}{h} \\ & =\lim\limits_{h \to 0} \frac{x \sin x(\cos h-1)}{h}+\lim\limits_{h \to 0} x \cos x \frac{\sin h}{h}+\lim\limits_{h \to 0}(\sin x \cos h+\sin h \cos x) \\ & =x \cos x+\sin x \end{aligned} $

उदाहरण 21 व्युत्पन्न की गणना कीजिए

(i) $f(x)=\sin 2 x$

(ii) $g(x)=\cot x$

हल (i) त्रिकोणमितीय सूत्र याद कीजिए $\sin 2 x=2 \sin x \cos x$. इस प्रकार

$ \begin{aligned} \frac{d f(x)}{d x} & =\frac{d}{d x}(2 \sin x \cos x)=2 \frac{d}{d x}(\sin x \cos x) \\ \\ & =2[(\sin x)^{\prime} \cos x+\sin x(\cos x)^{\prime}] \\ \\ & =2[(\cos x) \cos x+\sin x(-\sin x)] \\ \\ & =2(\cos ^{2} x-\sin ^{2} x) \end{aligned} $

(ii) परिभाषा से, $g(x)=\cot x=\frac{\cos x}{\sin x}$। हम इस फलन पर जहाँ-जहाँ यह परिभाषित है, भागफल नियम का प्रयोग करते हैं। $\frac{d g}{d x}=\frac{d}{d x}(\cot x)=\frac{d}{d x}(\frac{\cos x}{\sin x})$ $ \begin{aligned} & =\frac{(\cos x)^{\prime}(\sin x)-(\cos x)(\sin x)^{\prime}}{(\sin x)^{2}} \ & =\frac{(-\sin x)(\sin x)-(\cos x)(\cos x)}{(\sin x)^{2}} \ & =-\frac{\sin ^{2} x+\cos ^{2} x}{\sin ^{2} x}=-cosec^{2} x \end{aligned} $

वैकल्पिक रूप से, यह इसे यह देखकर भी निकाला जा सकता है कि $\cot x=\frac{1}{\tan x}$। यहाँ हम इस तथ्य का प्रयोग करते हैं कि $\tan x$ का अवकलज $\sec ^{2} x$ है, जिसे हमने उदाहरण 17 में देखा था, और यह भी कि अचर फलन का अवकलज 0 होता है।

$ \begin{aligned} \frac{d g}{d x} & =\frac{d}{d x}(\cot x)=\frac{d}{d x}(\frac{1}{\tan x}) \ & =\frac{(1)^{\prime}(\tan x)-(1)(\tan x)^{\prime}}{(\tan x)^{2}} \ & =\frac{(0)(\tan x)-(\sec x)^{2}}{(\tan x)^{2}} \ & =\frac{-\sec ^{2} x}{\tan ^{2} x}=-cosec^{2} x \end{aligned} $

उदाहरण 22 निम्नलिखित का अवकलज ज्ञात कीजिए

(i) $\frac{x^{5}-\cos x}{\sin x}$

(ii) $\frac{x+\cos x}{\tan x}$

हल (i) मान लीजिए $h(x)=\frac{x^{5}-\cos x}{\sin x}$। हम इस फलन पर जहाँ-जहाँ यह परिभाषित है, भागफल नियम का प्रयोग करते हैं।

$ h^{\prime}(x)=\frac{(x^{5}-\cos x)^{\prime} \sin x-(x^{5}-\cos x)(\sin x)^{\prime}}{(\sin x)^{2}} $

$ \begin{aligned} & =\frac{(5 x^{4}+\sin x) \sin x-(x^{5}-\cos x) \cos x}{\sin ^{2} x} \ & =\frac{-x^{5} \cos x+5 x^{4} \sin x+1}{(\sin x)^{2}} \end{aligned} $

(ii) हम फलन $\frac{x+\cos x}{\tan x}$ पर भागफल नियम का प्रयोग करते हैं जहाँ भी यह परिभाषित है।

$ \begin{aligned} h^{\prime}(x) & =\frac{(x+\cos x)^{\prime} \tan x-(x+\cos x)(\tan x)^{\prime}}{(\tan x)^{2}} \ & =\frac{(1-\sin x) \tan x-(x+\cos x) \sec ^{2} x}{(\tan x)^{2}} \end{aligned} $

सारांश

किसी बिंदु के बाईं ओर के बिंदुओं द्वारा निर्धारित मान के अनुसार फलन का प्रत्याशित मान उस बिंदु पर फलन का बायाँ पक्ष सीमा निर्धारित करता है। इसी प्रकार दायाँ पक्ष सीमा।

किसी बिंदु पर फलन की सीमा बायाँ और दायाँ पक्ष सीमाओं की सामान्य मान है, यदि वे मेल खाते हैं।

किसी फलन $f$ और वास्तविक संख्या $a$ के लिए, $\lim\limits_{x \to a} f(x)$ और $f(a)$ समान नहीं हो सकते (वास्तव में, एक परिभाषित हो सकता है और दूसरा नहीं)।

फलनों $f$ और $g$ के लिए निम्नलिखित सत्य है:

$ \begin{aligned} & \lim\limits_{x \to a}[f(x) \pm g(x)]=\lim\limits_{x \to a} f(x) \pm \lim\limits_{x \to a} g(x) \ \ & \lim\limits_{x \to a}[f(x) \cdot g(x)]=\lim\limits_{x \to a} f(x) \lim\limits_{x \to a} g(x) \ \ & \lim\limits_{x \to a}[\frac{f(x)}{g(x)}]=\frac{\lim\limits_{x \to a} f(x)}{\lim\limits_{x \to a} g(x)} \end{aligned} $

निम्नलिखित कुछ मानक सीमाएँ हैं

$ \lim\limits_{x \to a} \frac{x^{n}-a^{n}}{x-a}=n a^{n-1} $

$ \begin{aligned} & \lim\limits_{x \to 0} \frac{\sin x}{x}=1 \ & \lim\limits_{x \to 0} \frac{1-\cos x}{x}=0 \end{aligned} $

फलन $f$ का $a$ पर अवकलज निम्नलिखित द्वारा परिभाषित है

$ f^{\prime}(a)=\lim\limits_{h \to 0} \frac{f(a+h)-f(a)}{h} $

किसी फलन $f$ का किसी बिंदु $x$ पर अवकलज इस प्रकार परिभाषित है

$ f^{\prime}(x)=\frac{d f(x)}{d x}=\lim\limits_{h \to 0} \frac{f(x+h)-f(x)}{h} $

फलनों $u$ और $v$ के लिए निम्नलिखित सत्य हैं:

$ \begin{aligned} & (u \pm v)^{\prime}=u^{\prime} \pm v^{\prime} \ & (u v)^{\prime}=u^{\prime} v+u v^{\prime} \ & (\frac{u}{v})^{\prime}=\frac{u^{\prime} v-u v^{\prime}}{v^{2}} \text{ बशर्ते सभी परिभाषित हों। } \end{aligned} $

निम्नलिखित कुछ मानक अवकलज हैं।

$ \begin{aligned} & \frac{d}{d x}(x^{n})=n x^{n-1} \ & \frac{d}{d x}(\sin x)=\cos x \ & \frac{d}{d x}(\cos x)=-\sin x \end{aligned} $

ऐतिहासिक टिप्पणी

गणित के इतिहास में दो नाम कलन की खोज का श्रेय साझा करने के लिए प्रमुख हैं, आइज़ैक न्यूटन (1642 - 1727) और जी.डब्ल्यू. लाइबनिट्ज़ (1646 - 1717)। इन दोनों ने स्वतंत्र रूप से सत्रहवीं शताब्दी के आसपास कलन का आविष्कार किया। कलन के आगमन के बाद कई गणितज्ञों ने इसके आगे के विकास में योगदान दिया। कठोर अवधारणा मुख्यतः महान गणितज्ञों ए.एल. कोशी, जे.एल. लाग्रांज और कार्ल वीरस्ट्रास को दी जाती है। कोशी ने कलन की वह नींव रखी जिसे हम आजकल अपनी पाठ्यपुस्तकों में सामान्य रूप से स्वीकार करते हैं। कोशी ने डी’अलम्बर्ट की सीमा अवधारणा का उपयोग किसी फलन के अवकलज को परिभाषित करने के लिए किया। सीमा की परिभाषा से प्रारंभ करते हुए कोशी ने उदाहरण दिए जैसे $\alpha=0$ के लिए $\frac{\sin \alpha}{\alpha}$ की सीमा। उसने $\frac{\Delta y}{\Delta x}=\frac{f(x+i)-f(x)}{i}$ लिखा, और $i \to 0$ के लिए सीमा को “फलन डिरिवे, $y^{\prime}$ for $f^{\prime}(x)$” कहा।

1900 से पहले यह सोचा जाता था कि कलन सिखाना काफी कठिन है। इसलिए कलन युवाओं की पहुँच से परे हो गया। लेकिन ठीक 1900 में इंग्लैंड में जॉन पेरी और अन्य लोगों ने यह विचार फैलाना प्रारंभ किया कि कलन की आवश्यक विचारधाराएँ और विधियाँ सरल हैं और इन्हें विद्यालयों में भी पढ़ाया जा सकता है। एफ.एल. ग्रिफिन ने प्रथम वर्ष के विद्यार्थियों को कलन पढ़ाने की अग्रणी भूमिका निभाई। इसे उन दिनों का सबसे साहसी कार्य माना गया।

आज न केवल गणित बल्कि कई अन्य विषय जैसे भौतिकी, रसायन विज्ञान, अर्थशास्त्र और जैविक विज्ञान भी कलन के फलों का आनंद उठा रहे हैं।