अध्याय 02 संबंध और फलन
Subject Hub
सामान्य Learning Resources
गणित सभी भौतिक अनुसंधानों का अनिवार्य साधन है। - बर्टेलोट
2.1 प्रस्तावना
गणित का अधिकांश भाग एक प्रतिरूप खोजने के बारे में है — मात्राओं के बीच एक पहचानने योग्य सम्बन्ध जो परिवर्तित होती हैं। हमारे दैनिक जीवन में हम ऐसे अनेक प्रतिरूपों से मिलते हैं जो सम्बन्धों को चित्रित करते हैं जैसे भाई और बहन, पिता और पुत्र, शिक्षक और विद्यार्थी। गणित में भी हम अनेक सम्बन्धों से मिलते हैं जैसे संख्या $m$ संख्या $n$ से छोटी है, रेखा $l$ रेखा $m$ के समानान्तर है, समुच्चय $A$ समुच्चय $B$ का उपसमुच्चय है। इन सभी में हम देखते हैं कि एक सम्बन्ध में वस्तुओं के युग्म निश्चित क्रम में सम्मिलित होते हैं। इस अध्याय में हम सीखेंगे कि दो समुच्चयों से वस्तुओं के युग्मों को कैसे जोड़ा जाए और फिर युग्म में दो वस्तुओं के बीच सम्बन्ध प्रस्तुत किया जाए। अन्ततः हम ऐसे विशेष सम्बन्धों के बारे में सीखेंगे जो फलन बनने के योग्य ठहरेंगे।

G.W.लाइबनिट्ज (1646-1716 ई.)
गणित में फलन की संकल्पना अत्यन्त महत्वपूर्ण है क्योंकि यह एक मात्रा के साथ दूसरी मात्रा के गणितीय रूप से सटीक पत्र-व्यवहार को समेट लेती है।
2.2 समुच्चयों का कार्तीय गुणनफल
मान लीजिए A रंगों का एक समुच्चय है जिसमें 2 रंग हैं और B वस्तुओं का एक समुच्चय है जिसमें 3 वस्तुएँ हैं, अर्थात्
$$ A=\{\text { लाल, नीला }\} \text{ और } B=\{b, c, s\} \text{, } $$
जहाँ $b$, $c$ और $s$ क्रमशः एक विशिष्ट बैग, कोट और कमीज़ को दर्शाते हैं।
इन दो समुच्चयों से रंगीन वस्तुओं के कितने युग्म बनाए जा सकते हैं?
बहुत ही क्रमबद्ध तरीके से आगे बढ़ते हुए, हम देख सकते हैं कि नीचे दिए गए 6 भिन्न-भिन्न युग्म बनेंगे:
(red, $b$ ), (red, $c$ ), (red, $s$ ), (blue, $b$ ), (blue, $c$ ), (blue, $s$ ).
इस प्रकार हमें 6 भिन्न वस्तुएँ प्राप्त होती हैं (चित्र 2.1)।

चित्र 2.1
आइए हम अपनी पिछली कक्षाओं से याद करें कि किसी भी दो समुच्चयों $P$ और $Q$ से लिए गए अनुरूपित युग्म तत्वों का एक युग्म होता है जिसे छोटे कोष्ठकों में लिखा जाता है और एक विशिष्ट क्रम में साथ-साथ समूहित किया जाता है, अर्थात् $(p, q), p \in P$ और $q \in Q$। यह निम्नलिखित परिभाषा की ओर ले जाता है:
परिभाषा 1 दो अरिक्त समुच्चय $P$ और $Q$ दिए गए हैं। कार्तीय गुणनफल $P \times Q$ ऐसे सभी अनुरूपित युग्मों का समुच्चय है जो $P$ और $Q$ के तत्वों से बने होते हैं, अर्थात्
$$ P \times Q=\{(p, q): p \in P, q \in Q\} $$
यदि या तो $P$ या $Q$ रिक्त समुच्चय है, तो $P \times Q$ भी रिक्त समुच्चय होगा, अर्थात् $P \times Q=\phi$
ऊपर दिए गए चित्रण से हम नोट करते हैं कि
$A \times B=\{(red, b),($ red,$c),($ red,$s),($ blue,$b),($ blue,$c),($ blue,$s)\}$।
पुनः, दो समुच्चयों पर विचार करें:
$A=\{DL, MP, KA\}$, जहाँ DL, MP, KA क्रमशः दिल्ली, मध्य प्रदेश और कर्नाटक को दर्शाते हैं और B $=\{01,02, 03 \}$ DL, MP और KA द्वारा जारी किए गए वाहनों के लाइसेंस प्लेटों के कोडों को दर्शाता है।
यदि तीन राज्य, दिल्ली, मध्य प्रदेश और कर्नाटक वाहनों के लाइसेंस प्लेट के लिए कोड बना रहे हों, इस प्रतिबंध के साथ कि कोड समुच्चय A के एक अवयव से शुरू हो, तो इन समुच्चयों से उपलब्ध युग्म कौन-कौन से हैं और ऐसे कुल कितने युग्म होंगे (चित्र 2.2)?

चित्र 2.2
उपलब्ध युग्म हैं:$(\mathrm{DL}, 01),(\mathrm{DL}, 02),(\mathrm{DL}, 03),(\mathrm{MP}, 01),(\mathrm{MP}, 02)$, $(\mathrm{MP}, 03),(\mathrm{KA}, 01),(\mathrm{KA}, 02),(\mathrm{KA}, 03)$ और समुच्चय A और समुच्चय B का कार्तीय गुणनफल $\mathrm{A} \times \mathrm{B}=\{(\mathrm{DL}, 01),(\mathrm{DL}, 02),(\mathrm{DL}, 03),(\mathrm{MP}, 01),(\mathrm{MP}, 02),(\mathrm{MP}, 03),(\mathrm{KA}, 01),(\mathrm{KA}, 02)$, $(\mathrm{KA}, 03)\} \text {. }$
इसमें स्पष्ट देखा जा सकता है कि कार्तीय गुणनफल में 9 युग्म होंगे, क्योंकि प्रत्येक समुच्चय A और B में 3 अवयव हैं। इससे हमें 9 संभावित कोड प्राप्त होते हैं। यह भी ध्यान दें कि इन अवयवों को जोड़ने का क्रम अत्यंत महत्वपूर्ण है। उदाहरण के लिए, कोड (DL, 01) कोड $(01, DL)$ के समान नहीं होगा।
अंतिम उदाहरण के तौर पर, दो समुच्चयों $A=\{a_1, a_2\}$ और $B=\{b_1, b_2, b_3, b_4\}$ पर विचार करें (चित्र 2.3)।
$A \times B=\{(a_1, b_1),(a_1, b_2),(a_1, b_3),(a_1, b_4),(a_2, b_1),(a_2, b_2),(a_2, b_3),(a_2, b_4)\} .$
इस प्रकार बने 8 क्रमित युग्म तल में बिन्दुओं की स्थिति को निरूपित कर सकते हैं यदि A और B वास्तविक संख्याओं के समुच्चय के उपसमुच्चय हों और यह स्पष्ट है कि स्थिति $(a_1, b_2)$ वाला बिन्दु स्थिति $(b_2, a_1)$ वाले बिन्दु से भिन्न होगा।
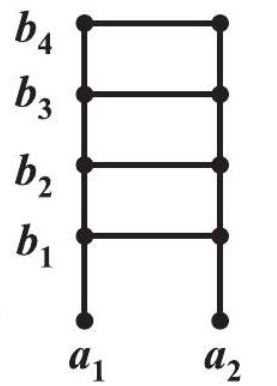
आकृति 2.3
टिप्पणियाँ
(i) दो क्रमित युग्म तभी बराबर होते हैं जबकि संगत प्रथम अवयव बराबर हों और द्वितीय अवयव भी बराबर हों।
(ii) यदि A में p अवयव और B में q अवयव हों, तो A × B में p q अवयव होंगे, अर्थात् यदि n(A)=p और n(B)=q, तो n(A × B)=p q।
(iii) यदि A और B अरिक्त समुच्चय हों और या तो A या B एक अनंत समुच्चय हो, तो A × B भी अनंत समुच्चय होगा।
(iv) A × A × A={(a, b, c): a, b, c ∈ A}। यहाँ (a, b, c) को एक क्रमित त्रिक कहा जाता है।
उदाहरण 1 यदि (x+1, y-2)=(3,1), तो x और y के मान ज्ञात कीजिए।
हल चूँकि क्रमित युग्म बराबर हैं, संगत अवयव बराबर हैं।
इसलिए
$ x+1=3 \text{ और } y-2=1 \text{।} $
हल करने पर हम पाते हैं $\quad x=2$ और y=3।
उदाहरण 2 यदि P={a, b, c} और Q={r}, तो समुच्चय P × Q और Q × P बनाइए।
क्या ये दोनों गुणनफल बराबर हैं?
हल कार्तीय गुणनफल की परिभाषा से,
$$ P \times Q=\{(a, r),(b, r),(c, r)\} \text { और } Q \times P=\{(r, a),(r, b),(r, c)\} $$
चूँकि, क्रमित युग्मों की समता की परिभाषा के अनुसार, युग्म $(a, r)$ युग्म $(r, a)$ के बराबर नहीं है, हम निष्कर्ष निकालते हैं कि $P \times Q \neq Q \times P$।
हालाँकि, प्रत्येक समुच्चय में अवयवों की संख्या समान होगी।
उदाहरण 3 मान लीजिए $A=\{1,2,3\}, B=\{3,4\}$ और $C=\{4,5,6\}$ है। ज्ञात कीजिए
(i) $A \times(B \cap C)$
(ii) $(A \times B) \cap(A \times C)$
(iii) $A \times(B \cup C)$
(iv) $(A \times B) \cup(A \times C)$
हल (i) दो समुच्चयों के सर्वनिष्ठ की परिभाषा से, $(B \cap C)=\{4\}$।
इसलिए, $A \times(B \cap C)=\{(1,4),(2,4),(3,4)\}$।
(ii) अब $(A \times B)=\{(1,3),(1,4),(2,3),(2,4),(3,3),(3,4)\}$ और $(A \times C)=\{(1,4),(1,5),(1,6),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6)\}$
इसलिए, $(A \times B) \cap(A \times C)=\{(1,4),(2,4),(3,4)\}$।
(iii) चूँकि, $\quad(B \cup C)=\{3,4,5,6\}$,
हमारे पास $\quad \mathrm{A} \times(\mathrm{B} \cup \mathrm{C})=\{(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,3)$, $(3,4),(3,5),(3,6)\}$ है।
(iv) ऊपर भाग (ii) से प्राप्त समुच्चयों $A \times B$ और $A \times C$ का प्रयोग करते हुए, हम प्राप्त करते हैं $(A \times B) \cup(A \times C)=\{(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6)$, $(3,3),(3,4),(3,5),(3,6)\}$।
उदाहरण 4 यदि $P=\{1,2\}$ है, तो समुच्चय $P \times P \times P$ बनाइए।
हल हमारे पास, $ P \times P \times P=\{(1,1,1),(1,1,2),(1,2,1),(1,2,2),(2,1,1),(2,1,2),(2,2,1)$, $(2,2,2)\} $ है।
उदाहरण 5 यदि $\mathbf{R}$ सभी वास्तविक संख्याओं का समुच्चय है, तो कार्टेशियन गुणनफल $\mathbf{R} \times \mathbf{R}$ और $\mathbf{R} \times \mathbf{R} \times \mathbf{R}$ क्या निरूपित करते हैं?
हल कार्टेशियन गुणनफल $\mathbf{R} \times \mathbf{R}$ समुच्चय $\mathbf{R} \times \mathbf{R}=\{(x, y): x, y \in \mathbf{R}\}$ को निरूपित करता है जो द्वि-आयामी समतल में सभी बिंदुओं के निर्देशांक निरूपित करता है और कार्टेशियन गुणनफल $\mathbf{R} \times \mathbf{R} \times \mathbf{R}$ समुच्चय $\mathbf{R} \times \mathbf{R} \times \mathbf{R}=\{(x, y, z): x, y, z \in \mathbf{R}\}$ को निरूपित करता है जो त्रि-आयामी समतल में सभी बिंदुओं के निर्देशांक निरूपित करता है।
उदाहरण 6 यदि $A \times B=\{(p, q),(p, r),(m, q),(m, r)\}$, तो $A$ और $B$ ज्ञात कीजिए।
हल
$$ \begin{aligned} & A=\text { प्रथम अवयवों का समुच्चय }=\{p, m\} \\ & B=\text { द्वितीय अवयवों का समुच्चय }=\{q, r\} . \end{aligned} $$
2.1 संबंध
दो समुच्चयों $P=\{a, b, c\}$ और $Q=\{$ अली, भानु, बिनॉय, चंद्र, दिव्या $\}$ पर विचार कीजिए।
$P$ और $Q$ का कार्टेशियन गुणनफल 15 क्रमित युगल रखता है जिन्हें इस प्रकार सूचीबद्ध किया जा सकता है $P \times Q=\{(a, \text{अली})$, (a, भानु), (a, बिनॉय), …, (c, दिव्या) $\}$।

चित्र 2.4
हम अब $P \times Q$ का एक उपसमुच्चय प्राप्त कर सकते हैं यदि प्रत्येक क्रमित युग्म $(x, y)$ के प्रथम अवयव $x$ और द्वितीय अवयव $y$ के बीच एक संबंध $R$ परिभाषित करें जैसा कि
$R=\{(x, y): x$ नाम $y$ का प्रथम अक्षर है, $x \in P, y \in Q\}$।
तब $R=\{(a, Ali),(b, Bhanu),(b, Binoy),(c$, Chandra $)\}$
इस संबंध $R$ (जिसे तीर आरेख कहा जाता है) की एक दृश्य प्रस्तुति आकृति 2.4 में दिखाई गई है।
परिभाषा 2 एक अ-रिक्त समुच्चय $A$ से एक अ-रिक्त समुच्चय $B$ तक एक संबंध $R$ कार्तीय गुणनफल $A \times B$ का एक उपसमुच्चय होता है। यह उपसमुच्चय $A \times B$ के क्रमित युग्मों के प्रथम और द्वितीय अवयवों के बीच एक संबंध वर्णित करके प्राप्त किया जाता है। द्वितीय अवयव को प्रथम अवयव की प्रतिबिंब कहा जाता है।
परिभाषा 3 एक समुच्चय $A$ से समुच्चय $B$ तक एक संबंध $R$ के सभी क्रमित युग्मों के प्रथम अवयवों का समुच्चय संबंध $R$ का प्रांत (domain) कहलाता है।
परिभाषा 4 एक समुच्चय $A$ से समुच्चय $B$ तक एक संबंध $R$ के सभी द्वितीय अवयवों का समुच्चय संबंध $R$ का परिसर (range) कहलाता है। संपूर्ण समुच्चय $B$ को संबंध $R$ का सह-प्रांत (codomain) कहा जाता है। ध्यान दें कि परिसर $\subset$ सह-प्रांत।
टिप्पणियाँ (i) एक संबंध को बीजगणितीय रूप से या तो रोस्टर विधि द्वारा या सेट-निर्माण विधि द्वारा प्रस्तुत किया जा सकता है।
(ii) तीर आरेख एक संबंध की दृश्य प्रस्तुति होता है।
उदाहरण 7 मान लीजिए $A=\{1,2,3,4,5,6\}$। एक संबंध $R$ को $A$ से $A$ तक इस प्रकार परिभाषित करें $R=\{(x, y): y=x+1\}$
(i) इस संबंध को तीर आरेख द्वारा चित्रित कीजिए।
(ii) $R$ का प्रांत, सह-प्रांत और परिसर लिखिए।
हल (i) संबंध की परिभाषा के अनुसार,
(R={(1,2),(2,3),(3,4),(4,5),(5,6)})।
संगत तीर आरेख चित्र 2.5 में दिखाया गया है।

चित्र 2.5
(ii) हम देख सकते हैं कि प्रांत (={1,2,3,4,5})
इसी प्रकार, परिसर (={2,3,4,5,6}) और सह-प्रांत (={1,2,3,4,5,6})।
उदाहरण 8 चित्र 2.6 समुच्चयों (P) और (Q) के बीच एक संबंध दिखाता है। इस संबंध को (i) समुच्चय-निर्माण रूप में, (ii) रोस्टर रूप में लिखिए। इसका प्रांत और परिसर क्या है?

चित्र 2.6
हल यह स्पष्ट है कि संबंध (R) है “(x), (y) का वर्ग है”।
(i) समुच्चय-निर्माण रूप में, (R={(x, y): x), (y) का वर्ग है, (x \in P, y \in \mathbf{Q}})
(ii) रोस्टर रूप में, (R={(9,3)), ((9,-3),(4,2),(4,-2),(25,5),(25,-5)})
इस संबंध का प्रांत ({4,9,25}) है।
इस संबंध का परिसर ({-2,2,-3,3,-5,5}) है।
ध्यान दीजिए कि अवयव 1 समुच्चय (P) के किसी भी अवयव से संबद्ध नहीं है। समुच्चय (Q) इस संबंध का सह-प्रांत है।
नोट - एक समुच्चय $A$ से एक समुच्चय $B$ तक परिभाषित कुल संबंधों की संख्या $A \times B$ के संभावित उपसमुच्चयों की संख्या होती है। यदि $n(A)=p$ और $n(B)=q$ है, तो $n(A \times B)=p q$ और कुल संबंधों की संख्या $2^{p q}$ होती है।
उदाहरण 9 मान लीजिए $A=\{1,2\}$ और $B=\{3,4\}$ है। A से B तक संबंधों की संख्या ज्ञात कीजिए।
हल हमारे पास,
$ A \times B=\{(1,3),(1,4),(2,3),(2,4)\} $
चूँकि $n(A \times B)=4$, $A \times B$ के उपसमुच्चयों की संख्या $2^{4}$ है। इसलिए, $A$ से $B$ तक संबंधों की संख्या $2^{4}$ होगी।
टिप्पणी एक संबंध $R$ जो $A$ से $A$ तक होता है, उसे $A$ पर एक संबंध भी कहा जाता है।
2.4 फलन
इस खंड में, हम संबंध के एक विशेष प्रकार को फलन कहते हैं, उसका अध्ययन करते हैं। यह गणित की सबसे महत्वपूर्ण अवधारणाओं में से एक है। हम किसी फलन को एक नियम के रूप में कल्पना कर सकते हैं, जो कुछ दिए गए तत्वों से नए तत्व उत्पन्न करता है। ‘मानचित्र’ या ‘मैपिंग’ जैसे कई शब्द फलन को दर्शाने के लिए प्रयुक्त होते हैं।
परिभाषा 5 एक संबंध $f$ जो समुच्चय $A$ से समुच्चय $B$ तक होता है, फलन कहलाता है यदि समुच्चय $A$ का प्रत्येक तत्व समुच्चय $B$ में एक और केवल एक छवि रखता है।
दूसरे शब्दों में, एक फलन $f$ एक ऐसा संबंध है जो किसी अरिक्त समुच्चय $A$ से किसी अरिक्त समुच्चय $B$ तक होता है, जिसका डोमेन $f$ का $A$ होता है और $f$ में कोई भी दो भिन्न क्रमित युग्म समान प्रथम तत्व नहीं रखते हैं।
यदि $f$ एक फलन है A से B तक और $(a, b) \in f$, तो $f(a)=b$, जहाँ $b$ को $f$ के अंतर्गत $a$ की छवि कहा जाता है और $a$ को $f$ के अंतर्गत $b$ की पूर्वछवि कहा जाता है।
फलन $f$ को $A$ से $B$ तक $f: A \rightarrow B$ द्वारा दर्शाया जाता है।
पिछले उदाहरणों को देखते हुए, हम आसानी से देख सकते हैं कि उदाहरण 7 में संबंध फलन नहीं है क्योंकि तत्व 6 का कोई प्रतिबिंब नहीं है।
पुनः, उदाहरण 8 में संबंध फलन नहीं है क्योंकि डोमेन के तत्व एक से अधिक प्रतिबिंबों से जुड़े हैं। इसी प्रकार, उदाहरण 9 में संबंध भी फलन नहीं है। (क्यों?) नीचे दिए गए उदाहरणों में, हम कई और संबंध देखेंगे जिनमें से कुछ फलन हैं और कुछ नहीं।
उदाहरण 10 मान लीजिए $\mathbf{N}$ प्राकृत संख्याओं का समुच्चय है और संबंध $R$ को $N$ पर इस प्रकार परिभाषित किया गया है कि $R=\{(x, y): y=2 x, x, y \in \mathbf{N}\}$।
$R$ का डोमेन, कोडोमेन और परिसर क्या है? क्या यह संबंध एक फलन है?
हल $R$ का डोमेन प्राकृत संख्याओं का समुच्चय $\mathbf{N}$ है। कोडोमेन भी $\mathbf{N}$ है। परिसर सम-प्राकृत संख्याओं का समुच्चय है।
चूँकि प्रत्येक प्राकृत संख्या $n$ का एक और केवल एक प्रतिबिंब है, यह संबंध एक फलन है।
उदाहरण 11 नीचे दिए गए प्रत्येक संबंध की जाँच कीजिए और प्रत्येक स्थिति में कारण देते हुए बताइए कि यह फलन है या नहीं?
(i) $R=\{(2,1),(3,1),(4,2)\}$,
(ii) $R=\{(2,2),(2,4),(3,3),(4,4)\}$
(iii) $R=\{(1,2),(2,3),(3,4),(4,5),(5,6),(6,7)\}$
हल (i) चूँकि 2, 3, 4, R के डोमेन के तत्व हैं जिनके अद्वितीय प्रतिबिंब हैं, यह संबंध $R$ एक फलन है।
(ii) चूँकि एक ही प्रथम अवयव 2 के अनुरूप दो भिन्न प्रतिबिम्ब 2 और 4 हैं, यह संबंध फलन नहीं है।
(iii) चूँकि प्रत्येक अवयव का एक और केवल एक प्रतिबिम्ब है, यह संबंध एक फलन है।
परिभाषा 6 एक फलन जिसका परिसर $R$ या इसकी कोई उपसमुच्चय हो, वास्तविक मान वाला फलन कहलाता है। इसके अतिरिक्त, यदि इसका प्रांत भी $R$ या $R$ का कोई उपसमुच्चय हो, तो इसे वास्तविक फलन कहा जाता है।
उदाहरण 12 मान लीजिए $\mathbf{N}$ प्राकृत संख्याओं का समुच्चय है। एक वास्तविक मान वाला फलन परिभाषित कीजिए
$f: \mathbf{N} \rightarrow \mathbf{N}$ द्वारा $f(x)=2 x+1$। इस परिभाषा का प्रयोग करके नीचे दी गई सारणी को पूर्ण कीजिए।
| $x$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| $y$ | $f(1)=\ldots$ | $f(2)=\ldots$ | $f(3)=\ldots$ | $f(4)=\ldots$ | $f(5)=\ldots$ | $f(6)=\ldots$ | $f(7)=\ldots$ |
हल पूर्ण की गई सारणी इस प्रकार है
| $x$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| $y$ | $f(1)=3$ | $f(2)=5$ | $f(3)=7$ | $f(4)=9$ | $f(5)=11$ | $f(6)=13$ | $f(7)=15$ |
2.4.1 कुछ फलन और उनके आलेख
(i) तत्समक फलन मान लीजिए $\mathbf{R}$ वास्तविक संख्याओं का समुच्चय है। वास्तविक मान वाला फलन $f: \mathbf{R} \rightarrow \mathbf{R}$ को $y=f(x)=x$ द्वारा प्रत्येक $x \in \mathbf{R}$ के लिए परिभाषित कीजिए। ऐसा फलन तत्समक फलन कहलाता है। यहाँ $f$ का प्रांत और परिसर $\mathbf{R}$ हैं। आलेख एक सरल रेखा है जैसा कि आकृति 2.8 में दिखाया गया है। यह मूल बिंदु से होकर जाती है।

चित्र 2.8
(ii) नियत फलन फलन $f: \mathbf{R} \rightarrow \mathbf{R}$ को $y=f(x)=c, x \in \mathbf{R}$ द्वारा परिभाषित करें जहाँ $c$ एक नियतांक है और प्रत्येक $x \in \mathbf{R}$ है। यहाँ $f$ का प्रांत $\mathbf{R}$ है और इसका परिसर $\{c\}$ है।

चित्र 2.9
यह आलेख $x$-अक्ष के समांतर एक रेखा है। उदाहरण के लिए, यदि प्रत्येक $x \in \mathbf{R}$ के लिए $f(x)=3$ है, तो इसका आलेख चित्र 2.9 में दिखाए अनुसार एक रेखा होगी।
(iii) बहुपद फलन एक फलन $f: \mathbf{R} \rightarrow \mathbf{R}$ बहुपद फलन कहलाता है यदि प्रत्येक $x$ के लिए $\mathbf{R}$ में, $y=f(x)=a_0+a_1 x+a_2 x^{2}+\ldots+a_{n} x^{n}$, जहाँ $n$ एक ऋणेतर पूर्णांक है और $a_0, a_1, a_2, \ldots, a_{n} \in \mathbf{R}$ हैं।
$f(x)=x^{3}-x^{2}+2$ और $g(x)=x^{4}+\sqrt{2} x$ द्वारा परिभाषित फलन बहुपद फलनों के कुछ उदाहरण हैं, जबकि $h$ द्वारा परिभाषित फलन $h(x)=x^{\frac{2}{3}}+2 x$ एक बहुपद फलन नहीं है।(क्यों?)
उदाहरण 13 फलन $f: \mathbf{R} \rightarrow \mathbf{R}$ को $y=f(x)=x^{2}, x \in \mathbf{R}$ द्वारा परिभाषित कीजिए। इस परिभाषा का उपयोग करके नीचे दी गई तालिका को पूर्ण कीजिए। इस फलन का प्रांत और परिसर क्या है? $f$ का आलेख खींचिए।
| $x$ | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|---|---|
| $y=f(x)=x^{2}$ |
हल पूर्ण की गई तालिका नीचे दी गई है:
| $x$ | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|---|---|
| $y=f(x)=x^{2}$ | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 |
$f$ का प्रांत $=\{x: x \in \mathbf{R}\}$। $f$ का परिसर $=\{x^{2}: x \in \mathbf{R}\}$। $f$ का आलेख आकृति 2.10 द्वारा दिया गया है

आकृति 2.10
उदाहरण 14 फलन $\boldsymbol{f}: \mathbf{R} \rightarrow \mathbf{R}$ जिसे $f(x)=x^{3}, x \in \mathbf{R}$ द्वारा परिभाषित किया गया है, का आलेख खींचिए।
हल हमारे पास
$f(0)=0, f(1)=1, f(-1)=-1, f(2)=8, f(-2)=-8, f(3)=27 ; f(-3)=-27$, आदि।
इसलिए, $f=\{(x, x^{3}): x \in \mathbf{R}\}$।
$f$ का आलेख आकृति 2.11 में दिया गया है।

आकृति 2.11
(iv) परिमेय फलन वे फलन होते हैं जो $\frac{f(x)}{g(x)}$ के रूप के होते हैं, जहाँ $f(x)$ और $g(x)$ चर $x$ के बहुपद फलन हैं और ये एक ऐसे डोमेन में परिभाषित होते हैं जहाँ $g(x) \neq 0$।
उदाहरण 15 वास्तविक मान वाला फलन $f: \mathbf{R}-\{0\} \rightarrow \mathbf{R}$ जो $f(x)=\frac{1}{x}$ द्वारा परिभाषित है, जहाँ $x \in \mathbf{R}-\{0\}$। इस परिभाषा का उपयोग करके नीचे दी गई सारणी को पूरा कीजिए। इस फलन का डोमेन और परिसर क्या है?
| $x$ | -2 | -1.5 | -1 | -0.5 | 0.25 | 0.5 | 1 | 1.5 | 2 |
|---|---|---|---|---|---|---|---|---|---|
| $y=\frac{1}{x}$ | $\ldots$ | $\ldots$ | $\ldots$ | $\ldots$ | $\ldots$ | $\ldots$ | $\ldots$ | $\ldots$ | $\ldots$ |
हल पूरी की गई सारणी इस प्रकार है
| $x$ | -2 | -1.5 | -1 | -0.5 | 0.25 | 0.5 | 1 | 1.5 | 2 |
|---|---|---|---|---|---|---|---|---|---|
| $y=\frac{1}{x}$ | -0.5 | -0.67 | -1 | -2 | 4 | 2 | 1 | 0.67 | 0.5 |
डोमेन सभी वास्तविक संख्याएँ हैं सिवाय 0 के और इसका परिसर भी सभी वास्तविक संख्याएँ हैं सिवाय 0 के। $f$ का ग्राफ Fig 2.12 में दिया गया है।

Fig 2.12
(v) मापांक फलन वह फलन $f: \mathbf{R} \rightarrow \mathbf{R}$ जिसे प्रत्येक $x \in \mathbf{R}$ के लिए $f(x)=|x|$ द्वारा परिभाषित किया गया है, मापांक फलन कहलाता है। प्रत्येक ऋणेतर मान के लिए $x, f(x)$ का मान $x$ के बराबर होता है। परंतु $x$ के ऋण मानों के लिए, $f(x)$ का मान $x$ के मान का ऋण होता है, अर्थात् $f(x)=\begin{cases}x,x \geq 0 \ -x, x <0 \end{cases}$

आकृति 2.13
(vi) साइनम फलन वह फलन $f: \mathbf{R} \rightarrow \mathbf{R}$ जिसे
$$ f(x)=\begin{cases} 1, \text { यदि } x>0 \ 0, \text { यदि } x=0 \ -1, \text { यदि } x<0 \end{cases} $$
$$ f(x)=|x| $$
आकृति 2.13 द्वारा परिभाषित किया गया है, साइनम फलन कहलाता है। साइनम फलन का प्रांत $\mathbf{R}$ है और परिसर समुच्चय $\{-1,0,1\}$ है। साइनम फलन का आलेख आकृति 2.14 द्वारा दिया गया है।

आकृति 2.14
$$ f(x)=\frac{|x|}{x}, x^{\prime} \quad 0 \text { और } 0 \text{ के लिए } x=0 $$
(vii) महत्तम पूर्णांक फलन वह फलन $f: \mathbf{R} \rightarrow \mathbf{R}$ जिसे $f(x)=[x], x \in \mathbf{R}$ द्वारा परिभाषित किया गया है, वह महत्तम पूर्णांक का मान ग्रहण करता है, जो $x$ से छोटा या उसके बराबर होता है। ऐसे फलन को महत्तम पूर्णांक फलन कहा जाता है।
$[x]$ की परिभाषा से हम देख सकते हैं कि
$$ \begin{aligned} & {[x]=-1 \text { for }-1 \leq x<0} \\ & {[x]=0 \text { for } 0 \leq x<1} \\ & {[x]=1 \text { for } 1 \leq x<2} \\ & {[x]=2 \text { for } 2 \leq x<3 \text { and }} \end{aligned} $$ इत्यादि।
फलन का आलेख Fig 2.15 में दिखाया गया है।

Fig 2.15
2.4.2 वास्तविक फलनों का बीजगणित
इस खंड में हम सीखेंगे कि दो वास्तविक फलनों को कैसे जोड़ा जाता है, एक वास्तविक फलन को दूसरे से कैसे घटाया जाता है, एक वास्तविक फलन को एक अदिश से (यहाँ अदिश से हमारा तात्पर्य एक वास्तविक संख्या से है) कैसे गुणा किया जाता है, दो वास्तविक फलनों को कैसे गुणा किया जाता है और एक वास्तविक फलन को दूसरे से कैसे विभाजित किया जाता है।
(i) दो वास्तविक फलनों का योग मान लीजिए $f: X \rightarrow \mathbf{R}$ और $g: X \rightarrow \mathbf{R}$ कोई दो वास्तविक फलन हैं, जहाँ $X \subset \mathbf{R}$। तब हम $(f+g): X \rightarrow \mathbf{R}$ को इस प्रकार परिभाषित करते हैं
$(f+g)(x)=f(x)+g(x)$, सभी $x \in \mathbf{X}$ के लिए।
(ii) एक वास्तविक फलन को दूसरे से घटाना मान लीजिए $f: X \rightarrow \mathbf{R}$ और $g: X \rightarrow \mathbf{R}$ कोई दो वास्तविक फलन हैं, जहाँ $\mathbf{X} \subset \mathbf{R}$। तब हम $(f-g): X \rightarrow \mathbf{R}$ को $(f-g)(x)=f(x)-g(x)$, सभी $x \in X$ के लिए, परिभाषित करते हैं।
(iii) स्केलर से गुणा माना $f: X \rightarrow \mathbf{R}$ एक वास्तविक मान फलन है और $\alpha$ एक स्केलर है। यहाँ स्केलर से हमारा तात्पर्य एक वास्तविक संख्या से है। तब गुणनफल $\alpha f$ एक ऐसा फलन है जो $X$ से $\mathbf{R}$ में परिभाषित होता है और $(\alpha f)(x)=\alpha f(x), x \in X$ द्वारा दिया जाता है।
(iv) दो वास्तविक फलनों का गुणा दो वास्तविक फलनों $f: \mathbf{X} \rightarrow \mathbf{R}$ और $g: X \rightarrow \mathbf{R}$ का गुणनफल (या गुणा) एक फलन $f g: X \rightarrow \mathbf{R}$ होता है जो $(f g)(x)=f(x) g(x)$ द्वारा परिभाषित होता है, सभी $x \in X$ के लिए।
इसे बिंदुवार गुणा भी कहा जाता है।
(v) दो वास्तविक फलनों का भागफल माना $f$ और $g$ दो वास्तविक फलन हैं जो $X \rightarrow \mathbf{R}$ से परिभाषित हैं, जहाँ $X \subset \mathbf{R}$। $f$ का $g$ से भागफल, जिसे $\frac{f}{g}$ द्वारा दर्शाया जाता है, एक फलन है जो $(\frac{f}{g})(x)=\frac{f(x)}{g(x)}$ द्वारा परिभाषित होता है, बशर्ते $g(x) \neq 0, x \in X$
उदाहरण 16 माना $f(x)=x^{2}$ और $g(x)=2 x+1$ दो वास्तविक फलन हैं। ज्ञात कीजिए
$$ (f+g)(x),(f-g)(x),(f g)(x),(\frac{f}{g})(x) $$
हल हमारे पास,
$$ \begin{aligned} & (f+g)(x)=x^{2}+2 x+1,(f-g)(x)=x^{2}-2 x-1, \\ & (f g)(x)=x^{2}(2 x+1)=2 x^{3}+x^{2},(\frac{f}{g})(x)=\frac{x^{2}}{2 x+1}, x \neq-\frac{1}{2} \end{aligned} $$
उदाहरण 17 माना $f(x)=\sqrt{x}$ और $g(x)=x$ दो फलन हैं जो अ-ऋणात्मक वास्तविक संख्याओं के समुच्चय पर परिभाषित हैं। $(f+g)(x),(f-g)(x),(f g)(x)$ और $(\frac{f}{g})(x)$ ज्ञात कीजिए।
हल हमारे पास
$$ \begin{aligned} & (f+g)(x)=\sqrt{x}+x,(f-g)(x)=\sqrt{x}-x, \ & (f g) x=\sqrt{x}(x)=x^{\frac{3}{2}} \text{ और }(\frac{f}{g})(x)=\frac{\sqrt{x}}{x}=x^{-\frac{1}{2}}, x \neq 0 \end{aligned} $$
विविध उदाहरण
उदाहरण 18 मान लीजिए $\mathbf{R}$ वास्तविक संख्याओं का समुच्चय है।
वास्तविक फलन को परिभाषित कीजिए
$$ f: \mathbf{R} \rightarrow \mathbf{R} \text{ द्वारा } f(x)=x+10 $$
और इस फलन का आलेख खींचिए।
हल यहाँ $f(0)=10, f(1)=11, f(2)=12, \ldots$, $f(10)=20$, आदि, और
$f(-1)=9, f(-2)=8, \ldots, f(-10)=0$ इत्यादि।
इसलिए, दिए गए फलन के आलेख का आकार चित्र 2.16 में दिखाए अनुसार होता है।

चित्र 2.16
टिप्पणी फलन $f$ जिसे $f(x)=m x+c$, $x \in \mathbf{R}$ द्वारा परिभाषित किया गया है, रैखिक फलन कहलाता है, जहाँ $m$ और $c$ नियतांक हैं। उपरोक्त फलन एक रैखिक फलन का उदाहरण है।
उदाहरण 19 मान लीजिए $R$ एक संबंध है $\mathbf{Q}$ से $\mathbf{Q}$ तक जो $R=\{(a, b): a, b \in \mathbf{Q}$ और $a-b \in \mathbf{Z}\}$ द्वारा परिभाषित है। दिखाइए कि
(i) $(a, a) \in R$ सभी $a \in \mathbf{Q}$ के लिए
(ii) $(a, b) \in R$ का तात्पर्य है कि $(b, a) \in R$
(iii) $(a, b) \in R$ और $(b, c) \in R$ का तात्पर्य है कि $(a, c) \in R$
हल (i) चूँकि, $a-a=0 \in \mathbf{Z}$, इसलिए यह सिद्ध होता है कि $(a, a) \in R$।
(ii) $(a, b) \in R$ का अर्थ है कि $a-b \in \mathbf{Z}$। इसलिए, $b-a \in \mathbf{Z}$। अतः, $(b, a) \in R$
(iii) $(a, b)$ और $(b, c) \in R$ का अर्थ है कि $a-b \in \mathbf{Z}$ और $b-c \in \mathbf{Z}$। इसलिए, $a-c=(a-b)+(b-c) \in \mathbf{Z}$। अतः, $(a, c) \in R$
उदाहरण 20 मान लीजिए $f=\{(1,1),(2,3),(0,-1),(-1,-3)\}$ एक रैखिक फलन है जो $\mathbf{Z}$ से $\mathbf{Z}$ में है। $f(x)$ ज्ञात कीजिए।
हल चूँकि $f$ एक रैखिक फलन है, $f(x)=m x+c$। साथ ही, चूँकि $(1,1),(0,-1) \in R$, $f(1)=m+c=1$ और $f(0)=c=-1$। इससे $m=2$ और $f(x)=2 x-1$ प्राप्त होता है।
उदाहरण 21 फलन $f(x)=\frac{x^{2}+3 x+5}{x^{2}-5 x+4}$ का प्रांत ज्ञात कीजिए।
हल चूँकि $x^{2}-5 x+4=(x-4)(x-1)$, फलन $f$ सभी वास्तविक संख्याओं के लिए परिभाषित है सिवाय $x=4$ और $x=1$ के। इसलिए $f$ का प्रांत $\mathbf{R}-\{1,4\}$ है।
उदाहरण 22 फलन $f$ इस प्रकार परिभाषित है
$$ f(x)= \begin{cases}1-x, & x<0 \ 1 & , x=0 \ x+1, & x>0\end{cases} $$
$f(x)$ का आलेख खींचिए।
हल यहाँ, $f(x)=1-x, x<0$, इससे प्राप्त होता है
$ \begin{aligned} & f(-4)=1-(-4)=5 \\ & f(-3)=1-(-3)=4 \\ & f(-2)=1-(-2)=3 \\ & f(-1)=1-(-1)=2 ; \text { आदि } \end{aligned} $
और $f(1)=2, f(2)=3, f(3)=4$
$f(4)=5$ और इसी प्रकार $f(x)=x+1, x>0$ के लिए।
इस प्रकार, $f$ का आलेख Fig 2.17 में दिखाए अनुसार है

Fig 2.17
सारांश
इस अध्याय में हमने संबंधों और फलनों के बारे में पढ़ा। इस अध्याय की मुख्य विशेषताएँ इस प्रकार हैं:
क्रमित युग्म तत्वों का एक युग्म जिसे विशेष क्रम में समूहित किया गया हो।
कार्तीय गुणनफल $A \times B$ दो समुच्चयों $A$ और $B$ का निम्न प्रकार से दिया जाता है
$A \times B=\{(a, b): a \in A, b \in B\}$
विशेष रूप से $\mathbf{R} \times \mathbf{R}=\{(x, y): x, y \in \mathbf{R}\}$
और $\mathbf{R} \times \mathbf{R} \times \mathbf{R}=\{(x, y, z): x, y, z \in \mathbf{R}\}$
यदि $(a, b)=(x, y)$, तो $a=x$ और $b=y$। यदि $n(A)=p$ और $n(B)=q$, तो $n(A \times B)=p q$।
$\Delta A \times \phi=\phi$
सामान्यतः, $A \times B \neq B \times A$।
संबंध एक संबंध $R$ एक समुच्चय $A$ से एक समुच्चय $B$ तक क्रमित युग्मों के कार्तीय गुणनफल $A \times B$ का एक उपसमुच्चय होता है जिसे $A \times B$ में उपस्थित क्रमित युग्मों के प्रथम तत्व $x$ और द्वितीय तत्व $y$ के बीच संबंध को वर्णित करके प्राप्त किया जाता है।
एक तत्व $x$ का प्रतिबिंब एक संबंध $R$ के अंतर्गत $y$ द्वारा दिया जाता है, जहाँ $(x, y) \in R$,
$R$ का प्रांत उन सभी प्रथम तत्वों का समुच्चय होता है जो संबंध $R$ के क्रमित युग्मों में होते हैं।
संबंध $R$ का परिसर उन सभी द्वितीय तत्वों का समुच्चय होता है जो संबंध $R$ के क्रमित युग्मों में होते हैं।
फलन एक फलन $f$ एक समुच्चय $A$ से एक समुच्चय $B$ तक संबंध का एक विशिष्ट प्रकार होता है जिसमें समुच्चय $A$ का प्रत्येक तत्व $x$ का समुच्चय $B$ में एक और केवल एक प्रतिबिंब $y$ होता है।
हम इसे $f: A \rightarrow B$ लिखते हैं, जहाँ $f(x)=y$।
$A$ फलन $f$ का प्रांत है और B फलन $f$ का सह-प्रांत है।
फलन का परिसर प्रतिबिंबों का समुच्चय होता है।
एक वास्तविक फलन का प्रांत और परिसर दोनों वास्तविक संख्याओं के समुच्चय या उसके किसी उपसमुच्चय होते हैं।
फलनों का बीजगणित फलनों $f: X \rightarrow \mathbf{R}$ और $g: X \rightarrow \mathbf{R}$ के लिए, हमारे पास
$$ \begin{aligned} & (f+g)(x)=f(x)+g(x), x \in X \\ & (f-g)(x)=f(x)-g(x), x \in X \\ & (f . g)(x) \quad=f(x) \cdot g(x), x \in X \\ & (k f)(x) \quad=k(f(x)), x \in X, \text{ जहाँ } k \text{ एक वास्तविक संख्या है।} \\ & (\frac{f}{g})(x)=\frac{f(x)}{g(x)}, x \in X, g(x) \neq 0 \end{aligned} $$
ऐतिहासिक टिप्पणी
FUNCTION शब्द पहली बार 1673 में गॉटफ्राइड विल्हेल्म लाइबनिट्ज़ (1646-1716) द्वारा लिखित लैटिन पांडुलिपि “Methodus tangentium inversa, seu de fuctionibus” में प्रकट हुआ; लाइबनिट्ज़ ने इस शब्द का प्रयोग गैर-विश्लेषणात्मक अर्थ में किया। उन्होंने फलन को “गणितीय कार्य” के संदर्भ में माना - “कर्मचारी” केवल एक वक्र था।
5 जुलाई 1698 को, जोहान बर्नौली ने लाइबनिट्ज़ को लिखे एक पत्र में पहली बार जानबूझकर फलन शब्द का विश्लेषणात्मक अर्थ में विशेष उपयोग निर्धारित किया। उस महीने के अंत में, लाइबनिट्ज़ ने अपनी स्वीकृति दिखाते हुए उत्तर दिया।
Function शब्द 1779 में चैंबर्स की साइक्लोपीडिया में अंग्रेज़ी में पाया गया: “The term function is used in algebra, for an analytical expression any way compounded of a variable quantity, and of numbers, or constant quantities”.



