“कलन विधि को एक कुंजी मानकर, गणित को प्रकृति के स्वरूप की व्याख्या में सफलतापूर्वक लगाया जा सकता है।” - व्हाइटहेड

6.1 प्रस्तावना

अध्याय 5 में हमने सीखा है कि संयुक्त फलनों, प्रतिलोम त्रिकोणमितीय फलनों, अंतर्निहित फलनों, घातांकी फलनों और लघुगणकीय फलनों का अवकलज कैसे ज्ञात किया जाता है। इस अध्याय में हम अवकलज के अनुप्रयोगों का अध्ययन विभिन्न विषयों—जैसे अभियांत्रिकी, विज्ञान, सामाजिक विज्ञान तथा अन्य क्षेत्रों—में करेंगे। उदाहरणतः हम सीखेंगे कि अवकलज का उपयोग (i) मात्राओं के परिवर्तन की दर ज्ञात करने, (ii) किसी वक्र के किसी बिंदु पर स्पर्श रेखा और अभिलंब रेखा के समीकरण खोजने, (iii) किसी फलन के आलेख पर मोड़ बिंदु खोजने में कैसे किया जाता है, जिससे हमें वे बिंदु मिलते हैं जहाँ फलन का स्थानिक रूप से अधिकतम या न्यूनतम मान होता है। हम यह भी देखेंगे कि किसी फलन वर्धमान या ह्रासमान होने के अंतराल कैसे ज्ञात करते हैं। अंततः हम अवकलज की सहायता से कुछ मात्राओं के सन्निकट मान भी निकालेंगे।

6.2 मात्राओं के परिवर्तन की दर

याद कीजिए कि अवकलज $\frac{ds}{dt}$ से हमारा तात्पर्य समय $t$ के सापेक्ष दूरी $s$ के परिवर्तन की दर से है। इसी प्रकार, जब भी कोई राशि $y$ किसी अन्य राशि $x$ के साथ किसी नियम $y=f(x)$ को संतुष्ट करते हुए परिवर्तित होती है, तो $\frac{dy}{dx}$ (या $f^{\prime}(x)$) $y$ के $x$ के सापेक्ष परिवर्तन की दर को दर्शाता है और $\frac{dy}{dx}_{x=x_0}$ (या $f^{\prime}(x_0)$) $x=x_0$ पर $y$ के $x$ के सापेक्ष परिवर्तन की दर को दर्शाता है।

आगे, यदि दो चर $x$ और $y$ किसी अन्य चर $t$ के सापेक्ष परिवर्तित हो रहे हैं, अर्थात् यदि $x=f(t)$ और $y=g(t)$ हैं, तो श्रृंखला नियम (Chain Rule) द्वारा

$$ \frac{dy}{dx}=\frac{dy}{dt} / \frac{dx}{dt}, \text{ यदि } \frac{dx}{dt} \neq 0 $$

इस प्रकार, $y$ के $x$ के सापेक्ष परिवर्तन की दर की गणना $y$ और $x$ दोनों के $t$ के सापेक्ष परिवर्तन की दर का उपयोग करके की जा सकती है।

आइए कुछ उदाहरणों पर विचार करें।

उदाहरण 1 जब $r=5 cm$ हो तो एक वृत्त के क्षेत्रफल की उसकी त्रिज्या $r$ के सापेक्ष प्रति सेकंड परिवर्तन की दर ज्ञात कीजिए।

हल त्रिज्या $r$ वाले वृत्त का क्षेत्रफल A द्वारा दिया जाता है $A=\pi r^{2}$। इसलिए, क्षेत्रफल A की उसकी त्रिज्या $r$ के सापेक्ष परिवर्तन की दर $\frac{dA}{dr}=\frac{d}{dr}(\pi r^{2})=2\pi r$ द्वारा दी जाती है। जब $r=5 cm$, $\frac{dA}{dr}=10\pi$। इस प्रकार, वृत्त का क्षेत्रफल $10\pi cm^{2}/s$ की दर से परिवर्तित हो रहा है।

उदाहरण 2 एक घन का आयाम 9 घन सेंटीमीटर प्रति सेकंड की दर से बढ़ रहा है। जब एक किनारे की लंबाई 10 सेंटीमीटर हो, तो पृष्ठ क्षेत्रफल कितनी तेजी से बढ़ रहा है?

हल मान लीजिए $x$ एक किनारे की लंबाई है, $V$ आयाम है और $S$ घन का पृष्ठ क्षेत्रफल है। तब, $V=x^{3}$ और $S=6 x^{2}$, जहाँ $x$ समय $t$ का फलन है।

अब $ \qquad \frac{d V}{d t}=9 cm^{3} / s$ (दिया गया है)

इसलिए $ \qquad 9=\frac{d V}{d t}=\frac{d}{d t}(x^{3})=\frac{d}{d x}(x^{3}) \cdot \frac{d x}{d t} \quad(\text{ श्रृंखला नियम से })$

या $ \qquad =3 x^{2} \cdot \frac{d x}{d t} $

अब $ \qquad \frac{d x}{d t}=\frac{3}{x^{2}} \tag{1}$

$$ \begin{array}{rlr} \frac{d S}{d t} & =\frac{d}{d t}\left(6 x^{2}\right)=\frac{d}{d x}\left(6 x^{2}\right) \cdot \frac{d x}{d t} & \text { (श्रृंखला नियम से) } \\ & =12 x \cdot\left(\frac{3}{x^{2}}\right)=\frac{36}{x} & \text { ((1) का उपयोग करते हुए) } \end{array} $$

अतः, जब $ x=10 \mathrm{~cm}, \frac{d S}{d t}=3.6 \mathrm{~cm}^{2} / \mathrm{s} $

उदाहरण 3 एक पत्थर को शांत झील में गिराया जाता है और तरंगें 4 सेमी प्रति सेकंड की गति से वृत्तों में आगे बढ़ती हैं। उस क्षण, जब वृत्ताकार तरंग की त्रिज्या 10 सेमी है, संलग्न क्षेत्रफल कितनी तेजी से बढ़ रहा है?

हल त्रिज्या $r$ वाले वृत्त का क्षेत्रफल $A$ द्वारा दिया गया है $A=\pi r^{2}$। इसलिए, क्षेत्रफल A में समय $t$ के साथ परिवर्तन की दर है

$$ \frac{d \mathrm{~A}}{d t}=\frac{d}{d t}\left(\pi r^{2}\right)=\frac{d}{d r}\left(\pi r^{2}\right) \cdot \frac{d r}{d t}=2 \pi r \frac{d r}{d t} $$

यह दिया गया है कि $\frac{d r}{d t}=4 \mathrm{~cm}$

इसलिए,
$ r=10 \mathrm{~cm} $
$ \frac{d \mathrm{~A}}{d t}=2 \pi(10)(4)=80 \pi $

इस प्रकार, घिरा हुआ क्षेत्रफल $80 \pi cm^{2} / s$ की दर से बढ़ रहा है, जब $r=10 cm$।

नोट $\frac{d y}{d x}$ सकारात्मक होता है यदि $y$, $x$ के बढ़ने पर बढ़ता है और ऋणात्मक होता है यदि $y$, $x$ के बढ़ने पर घटता है।

उदाहरण 4 आयत की लंबाई $x$, $3 cm /$ मिनट की दर से घट रही है और चौड़ाई $y$, $2 cm /$ मिनट की दर से बढ़ रही है। जब $x=10 cm$ और $y=6 cm$ है, तो (a) परिमाप और (b) आयत के क्षेत्रफल के परिवर्तन की दर ज्ञात कीजिए।

हल चूँकि लंबाई $x$ समय के सापेक्ष घट रही है और चौड़ाई $y$ समय के सापेक्ष बढ़ रही है, हमारे पास

$$ \frac{d x}{d t}=-3 \mathrm{~cm} / \mathrm{min} \text { या } \frac{d y}{d t}=2 \mathrm{~cm} / \mathrm{min} $$

(a) आयत का परिमाप $P$ निम्नलिखित द्वारा दिया जाता है

$$ \mathrm{P}=2(x+y) $$

इसलिए
$ \frac{d \mathrm{P}}{d t}=2\left(\frac{d x}{d t}+\frac{d y}{d t}\right)=2(-3+2)=-2 \mathrm{~cm} / \mathrm{min} $

(b) आयत का क्षेत्रफल $A$ निम्नलिखित द्वारा दिया जाता है

$ A=x \cdot y $

इसलिए $ \begin{aligned} \frac{d \mathrm{~A}}{d t} & =\frac{d x}{d t} \cdot y+x \cdot \frac{d y}{d t} \\ & =-3(6)+10(2)(\text { क्योंकि } x=10 \mathrm{~cm} \text{ और } y=6 \mathrm{~cm}) \\ & =2 \mathrm{~cm}^{2} / \mathrm{min} \end{aligned} $

उदाहरण 5 किसी वस्तु के $x$ इकाई उत्पादन से संबद्ध कुल लागत $C(x)$ रुपयों में निम्नलिखित है

$$ C(x)=0.005 x^{3}-0.02 x^{2}+30 x+5000 $$

3 इकाई उत्पादन पर सीमांत लागत ज्ञात कीजिए, जहाँ सीमांत लागत से तात्पर्य किसी भी उत्पादन स्तर पर कुल लागत की तात्क्षणिक परिवर्तन दर से है।

हल चूँकि सीमांत लागत कुल लागत का उत्पादन के सापेक्ष परिवर्तन दर है, इसलिए

$ \begin{aligned} \text{ सीमांत } \qquad \mathrm{MC} & =\frac{d \mathrm{C}}{d x}=0.005\left(3 x^{2}\right)-0.02(2 x)+30 \\ \text{ जब } \qquad \mathrm{MC} & =0.015\left(3^{2}\right)-0.04(3)+30 \\ & =0.135-0.12+30=30.015 \end{aligned} $

अतः अभीष्ट सीमांत लागत ₹ 30.02 (लगभग) है।

उदाहरण 6 किसी उत्पाद की $x$ इकाई बिक्री से प्राप्त कुल राजस्व रुपयों में $R(x)=3 x^{2}+36 x+5$ द्वारा दिया गया है। जब $x=5$ हो तो सीमांत राजस्व ज्ञात कीजिए, जहाँ सीमांत राजस्व से तात्पर्य किसी क्षण बेची गई वस्तुओं की संख्या के सापेक्ष कुल राजस्व के परिवर्तन की दर से है।

हल चूँकि सीमांत राजस्व कुल राजस्व का बेची गई इकाइयों की संख्या के सापेक्ष परिवर्तन दर है, इसलिए

$ \begin{aligned} \text{ सीमांत राजस्व } \qquad (MR) & =\frac{d R}{d x}=6 x+36 \end{aligned} $ $ \begin{aligned} \text{ जब } \qquad x & =5, MR=6(5)+36=66 \end{aligned} $

इसलिए, अभीष्ट सीमांत राजस्व ₹ 66 है।

6.3 वर्धमान और ह्रासमान फलन

इस खंड में हम अवकलन का उपयोग यह ज्ञात करने के लिए करेंगे कि कोई फलन वर्धमान है, ह्रासमान है या कोई नहीं।

फलन $f$ दिया गया है जो $f(x)=x^{2}, x \in \mathbf{R}$ द्वारा प्रदत्त है। इस फलन का ग्राफ एक परवलय है जैसा कि चित्र 6.1 में दिया गया है।

मूल के बाईं ओर के मान

$x$	$f(x)=x^{2}$
-2	4
$-\frac{3}{2}$	$\frac{9}{4}$
-1	1
$-\frac{1}{2}$	$\frac{1}{4}$
0	0

जैसे-जैसे हम बाईं ओर से दाईं ओर जाते हैं, ग्राफ की ऊँचाई घटती है

जैसे-जैसे हम बाईं ओर से दाईं ओर जाते हैं, ग्राफ की ऊँचाई बढ़ती है मूल के दाईं ओर के मान

x	$ f(x)=x^2 $
0	0
$ \frac{1}{4} $	$ \frac{1}{4} $
1	1
$ \frac{3}{2} $	$ \frac{9}{4} $
2	4

सबसे पहले मूल बिंदु के दाईं ओर के ग्राफ (चित्र 6.1) पर विचार करें। ध्यान दें कि जब हम ग्राफ के साथ बाएँ से दाएँ जाते हैं, तो ग्राफ की ऊँचाई लगातार बढ़ती है। इस कारण से, फलन को वास्तविक संख्याओं $x>0$ के लिए वर्धमान कहा जाता है।

अब मूल बिंदु के बाईं ओर के ग्राफ पर विचार करें और यहाँ ध्यान दें कि जब हम ग्राफ के साथ बाएँ से दाएँ जाते हैं, तो ग्राफ की ऊँचाई लगातार घटती है। परिणामस्वरूप, फलन को वास्तविक संख्याओं $x<0$ के लिए ह्रासमान कहा जाता है।

अब हम एक फलन के लिए निम्नलिखित विश्लेषणात्मक परिभाषाएँ देंगे जो किसी अंतराल पर वर्धमान या ह्रासमान है।

परिभाषा 1 मान लीजिए I एक ऐसा अंतराल है जो किसी वास्तविक मान फलन $f$ के प्रांत में सम्मिलित है। तब $f$ को निम्नलिखित कहा जाता है:

(i) I पर वर्धमान, यदि $x_1<x_2$ in $I \Rightarrow f(x_1)<f(x_2)$ सभी $x_1, x_2 \in I$ के लिए।

(ii) I पर ह्रासमान, यदि $x_1, x_2$ in $I \Rightarrow f(x_1)<f(x_2)$ सभी $x_1, x_2 \in I$ के लिए।

(iii) I पर नियत, यदि $f(x)=c$ सभी $x \in I$ के लिए, जहाँ $c$ एक नियतांक है।

(iv) I पर ह्रासमान, यदि $x_1<x_2$ in $I \Rightarrow f(x_1) \geq f(x_2)$ सभी $x_1, x_2 \in I$ के लिए।

(v) I पर कठोरतः ह्रासमान, यदि $x_1<x_2$ in $I \Rightarrow f(x_1)>f(x_2)$ सभी $x_1, x_2 \in I$ के लिए।

ऐसे फलनों के आलेखीय निरूपण के लिए चित्र 6.2 देखें।

अब हम परिभाषित करेंगे कि कोई फलन किसी बिंदु पर वर्धमान या ह्रासमान कब होता है।

परिभाषा 2 मान लीजिए (x_0) एक वास्तविक मान फलन (f) के परिभाषा क्षेत्र का एक बिंदु है। तब (f) को (x_0) पर बढ़ता हुआ, घटता हुआ कहा जाता है यदि एक खुला अंतराल (I) मौजूद है जिसमें (x_0) सम्मिलित है, ताकि (f) क्रमशः (I) में बढ़ता हुआ, घटता हुआ हो।

आइए बढ़ता हुआ फलन के मामले के लिए इस परिभाषा को स्पष्ट करें।

उदाहरण 7 दिखाइए कि (f(x)=7 x-3) द्वारा दिया गया फलन (\mathbf{R}) पर बढ़ता हुआ है।

हल मान लीजिए (x_1) और (x_2) कोई दो संख्याएँ (\mathbf{R}) में हैं। तब

[ \begin{aligned} x _{1}<x _{2} & \Rightarrow 7 x _{1}<7 x _{2} \ & \Rightarrow 7 x _{1}-3<7 x _{2}-3 \ & \Rightarrow f\left(x _{1}\right)<f\left(x _{2}\right) \end{aligned} ]

इस प्रकार, परिभाषा 1 द्वारा, यह अनुसरण करता है कि (f) सख्ती से (\mathbf{R}) पर बढ़ता हुआ है।

अब हम बढ़ते और घटते फलनों के लिए प्रथम अवकलज परीक्षण प्रस्तुत करेंगे। इस परीक्षण के प्रमाण के लिए अध्याय 5 में अध्ययित माध्य मान प्रमेय की आवश्यकता होती है।

प्रमेय 1 मान लीजिए (f) अंतराल ([a, b]) पर संतत है और खुले अंतराल ((a, b)) पर अवकलनीय है। तब

(a) (f) अंतराल ([a, b]) में बढ़ता हुआ है यदि प्रत्येक (x \in(a, b)) के लिए (f^{\prime}(x)>0) हो

(b) (f) अंतराल ([a, b]) में घटता हुआ है यदि प्रत्येक (x \in(a, b)) के लिए (f^{\prime}(x)<0) हो

(c) (f) अंतराल ([a, b]) में एक नियत फलन है यदि प्रत्येक (x \in(a, b)) के लिए (f^{\prime}(x)=0) हो

प्रमाण (a) मान लीजिए (x_1, x_2 \in[a, b]) ऐसे हैं कि (x_1<x_2) है।

तब, माध्य मान प्रमेय (अध्याय 5 में प्रमेय 8) द्वारा, (x_1) और (x_2) के बीच एक बिंदु (c) मौजूद है ताकि

$$ f\left(x _{2}\right)-f\left(x _{1}\right)=f^{\prime}(c)\left(x _{2}-x _{1}\right) $$

अर्थात् $\begin{array}{ll} f\left(x _{2}\right)-f\left(x _{1}\right)>0 & \left(\text { दिया गया है } f^{\prime}(c)>0\right) \end{array}$

अर्थात् $f(x_2)>f(x_1)$

इस प्रकार, हमारे पास है $x_1<x_2 \quad f(x_1) \quad f(x_2), \text{ सभी } x_1, x_2 \quad[a, b]$ के लिए

अतः, $f$ एक वर्धमान फलन है $[a, b]$ में।

भाग (b) और (c) के प्रमाण समान हैं। यह पाठक के अभ्यास के लिए छोड़ा गया है।

टिप्पणियाँ

एक अधिक व्यापक प्रमेय है, जो कहती है कि यदि $f \phi(x)>0$ अंतराल में बिन्दुओं को छोड़कर $x$ के लिए हो और $f$ अंतराल में संतत है, तो $f$ वर्धमान है। इसी प्रकार, यदि $f \phi(x)<0$ अंतराल में बिन्दुओं को छोड़कर $x$ के लिए हो और $f$ अंतराल में संतत है, तो $f$ ह्रासमान है।

उदाहरण 8 दिखाइए कि फलन $f$ जो दिया गया है

$\mathbf{R}$ पर वर्धमान है।

$$ f(x)=x^{3}-3 x^{2}+4 x, x \in \mathbf{R} $$

हल ध्यान दीजिए कि

$$ \begin{aligned} f^{\prime}(x) & =3 x^{2}-6 x+4 \\ & =3(x^{2}-2 x+1)+1 \\ & =3(x-1)^{2}+1>0, \mathbf{R} के प्रत्येक अंतराल में \end{aligned} $$

अतः, फलन $f$ वर्धमान है $\mathbf{R}$ पर।

उदाहरण 9 सिद्ध कीजिए कि फलन जो दिया गया है $f(x)=\cos x$

(a) $(0, \pi)$ में ह्रासमान है

(b) $(\pi, 2 \pi)$ में वर्धमान है, और

(c) $(0,2 \pi)$ में न तो वर्धमान है और न ही ह्रासमान है।

हल ध्यान दीजिए कि $f^{\prime}(x)=-\sin x$

(a) चूँकि प्रत्येक $x \in(0, \pi)$ के लिए, $\sin x>0$, हमारे पास $f^{\prime}(x)<0$ है और इसलिए $f$, $(0, \pi)$ में घट रही है।

(b) चूँकि प्रत्येक $x \in(\pi, 2 \pi)$ के लिए, $\sin x<0$, हमारे पास $f^{\prime}(x)>0$ है और इसलिए $f$, $(\pi, 2 \pi)$ में बढ़ रही है।

(c) स्पष्टतः (a) और (b) से ऊपर, $f$, $(0,2 \pi)$ में न तो बढ़ रही है और न ही घट रही है।

उदाहरण 10 वे अंतराल ज्ञात कीजिए जिनमें फलन $f$ दिया गया है $f(x)=x^{2}-4 x+6$ (a) बढ़ रहा है (b) घट रहा है

हल हमारे पास

$$ f(x)=x^{2}-4 x+6 $$ $ या \qquad f^{\prime}(x)=2 x-4 $

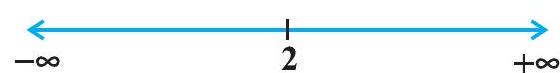
इसलिए, $f^{\prime}(x)=0$ देता है $x=2$. अब बिंदु $x=2$ वास्तविक रेखा को दो असंयुक्त अंतरालों में विभाजित करता है, अर्थात्, $(-\infty, 2)$ और $(2, \infty)$ (आकृति 6.3)। अंतराल $(-\infty, 2)$ में, $f^{\prime}(x)=2 x$ $-4<0$ है।

इसलिए, $f$ इस अंतराल में घट रही है। साथ ही, अंतराल $(2, \infty)$ में, $f^{\prime}(x)>0$ है और इसलिए फलन $f$ इस अंतराल में बढ़ रही है।

उदाहरण 11 वे अंतराल ज्ञात कीजिए जिनमें फलन $f$ दिया गया है $f(x)=4 x^{3}-6 x^{2}-72 x$ +30 (a) बढ़ रहा है (b) घट रहा है।

हल हमारे पास

$$ \text{ या } \quad \begin{aligned} f(x) & =4 x^{3}-6 x^{2}-72 x+30 \\ f^{\prime}(x) & =12 x^{2}-12 x-72 \\ & =12(x^{2}-x-6) \\ & =12(x-3)(x+2) \end{aligned} $$

इसलिए, $f^{\prime}(x)=0$ देता है $x=-2,3$। बिंदु $x=-2$ और $x=3$ वास्तविक रेखा को तीन असंयुक्त अंतरालों में विभाजित करते हैं, अर्थात्, $(-\infty,-2),(-2,3)$

आकृति 6.4 और $(3, \infty)$।

अंतरालों $(-\infty,-2)$ और $(3, \infty)$ में, $f^{\prime}(x)$ धनात्मक है जबकि अंतराल $(-2,3)$ में, $f^{\prime}(x)$ ऋणात्मक है। परिणामस्वरूप, फलन $f$ अंतरालों $(-\infty,-2)$ और $(3, \infty)$ में बढ़ रहा है जबकि फलन अंतराल $(-2,3)$ में घट रहा है। हालांकि, $f$ न तो $\mathbf{R}$ में बढ़ रहा है और न ही घट रहा है।

अंतराल	$ f’(x) $ का चिह्न	फलन $ f $ की प्रकृति
$ (\infty, -2) $	(-)(-)>0	$ f $ बढ़ रहा है
(-2,3)	(-)(+)<0	$ f $ घट रहा है
$ (3,\infty)$	(+)(+)>0	$ f $ बढ़ रहा है

उदाहरण 12 वे अंतराल ज्ञात कीजिए जिनमें फलन $f(x)=\sin 3 x, x \in 0, \frac{\pi}{2}$ (a) बढ़ रहा है (b) घट रहा है।

हल हमारे पास

$f(x) =\sin 3 x $

या $\quad f(x) =3 \cos 3 x$

इसलिए, $f^{\prime}(x)=0$ देता है $\cos 3 x=0$ जो बदले में देता है $3 x=\frac{\pi}{2}, \frac{3 \pi}{2}$ (चूँकि $x \in 0, \frac{\pi}{2}$ का अर्थ है $3 x \in[0, \frac{3 \pi}{2}]$)। इसलिए $x=\frac{\pi}{6}$ और $\frac{\pi}{2}$। बिंदु $x=\frac{\pi}{6}$ अंतराल $0, \frac{\pi}{2}$ को दो असंयुक्त अंतरालों $[0, \frac{\pi}{6})$ और $\frac{\pi}{6}, \frac{\pi}{2}$ में विभाजित करता है।

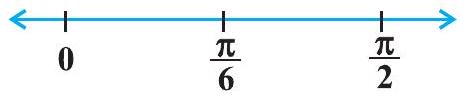
चित्र 6.5

अब, $f^{\prime}(x)>0$ सभी $x \in[0, \frac{\pi}{6})$ के लिए चूँकि $0 \leq x<\frac{\pi}{6} \Rightarrow 0 \leq 3 x<\frac{\pi}{2}$ और $f^{\prime}(x)<0$ सभी $x \in(\frac{\pi}{6}, \frac{\pi}{2})$ के लिए चूँकि $\frac{\pi}{6}<x<\frac{\pi}{2} \Rightarrow \frac{\pi}{2}<3 x<\frac{3 \pi}{2}$।

इसलिए, $f$ बढ़ रही है $[0, \frac{\pi}{6})$ में और घट रही है $(\frac{\pi}{6}, \frac{\pi}{2})$ में।

साथ ही, दी गई फलन $x=0$ और $x=\frac{\pi}{6}$ पर संतत है। इसलिए, प्रमेय 1 द्वारा, $f$ बढ़ रही है $[0, \frac{\pi}{6}]$ पर और घट रही है $[\frac{\pi}{6}, \frac{\pi}{2}]$ पर।

उदाहरण 13 वे अंतराल ज्ञात कीजिए जिनमें फलन $f$ जो दिया गया है

$ f(x)=\sin x+\cos x, 0 \leq x \leq 2 \pi $

बढ़ रही है या घट रही है।

हल हमारे पास है

$$ \begin{array}{lrlr} & f(x) & =\sin x+\cos x, \quad 0 \leq x \leq 2 \pi \\ \text{या }&f^{\prime}(x) & =\cos x-\sin x & \end{array} $$

अब $f^{\prime}(x)=0$ देता है $\sin x=\cos x$ जो देता है कि $x=\frac{\pi}{4}, \frac{5 \pi}{4}$ चूँकि $0 \leq x \leq 2 \pi$

बिंदु $x=\frac{\pi}{4}$ और $x=\frac{5 \pi}{4}$ अंतराल $[0,2 \pi]$ को तीन असंयुक्त अंतरालों में विभाजित करते हैं,

अर्थात्, $[0, \frac{\pi}{4}), \frac{\pi}{4}, \frac{5 \pi}{4}$ और $(\frac{5 \pi}{4}, 2 \pi]$।

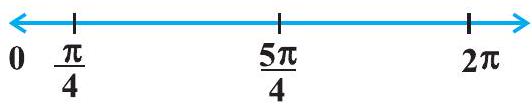
चित्र 6.6

ध्यान दें कि $f^{\prime}(x)>0$ यदि $x \in[0, \frac{\pi}{4}) \cup(\frac{5 \pi}{4}, 2 \pi]$

या $\quad f$ अंतरालों $[0, \frac{\pi}{4})$ और $(\frac{5 \pi}{4}, 2 \pi]$ में बढ़ रही है

इसके अतिरिक्त $\quad f^{\prime}(x)<0$ यदि $x \in \frac{\pi}{4}, \frac{5 \pi}{4}$

या $\quad f$ अंतराल $\frac{\pi}{4}, \frac{5 \pi}{4}$ में घट रही है

अंतराल	$ f $ ‘(x) का चिह्न	फलन की प्रकृति
[$ 0, \frac{\pi}{4} $]	>0	$ f $ बढ़ रही है
$ (\frac{\pi}{4}, \frac{5\pi}{4}) $	<0	$ f $ घट रही है
$ (\frac{5 \pi}{4},2\pi $	>0	$ f $ बढ़ रही है

6.4 उच्चतम और न्यूनतम

इस खण्ड में हम अवकलज की संकल्पना का प्रयोग विभिन्न फलनों के अधिकतम या न्यूनतम मानों की गणना करने के लिए करेंगे। वास्तव में, हम किसी फलन के आलेख के ‘मोड़ बिन्दुओं’ को ज्ञात करेंगे और इस प्रकार वे बिन्दु खोजेंगे जहाँ आलेख स्थानीय रूप से अपनी उच्चतम (या न्यूनतम) स्थिति तक पहुँचता है। ऐसे बिन्दुओं की जानकारी किसी दिए गए फलन के आलेख को बनाने में अत्यंत उपयोगी होती है। आगे, हम किसी फलन के निरपेक्ष अधिकतम तथा निरपेक्ष न्यूनतम को भी ज्ञात करेंगे जो अनेक प्रयुक्त समस्याओं के समाधान के लिए आवश्यक होते हैं।

आइए निम्नलिखित समस्याओं पर विचार करें जो दैनिक जीवन में उत्पन्न होती हैं।

(i) संतरे के पेड़ों के एक बगीचे से प्राप्त लाभ $P(x)=a x+b x^{2}$ द्वारा दिया गया है, जहाँ $a, b$ स्थिरांक हैं तथा $x$ प्रति एकड़ संतरे के पेड़ों की संख्या है। प्रति एकड़ कितने पेड़ लगाए जाएँ कि लाभ अधिकतम हो?

(ii) एक गेंद, 60 मीटर ऊँची इमारत से हवा में फेंकी जाती है, जो $h(x)=60+x-\frac{x^{2}}{60}$ द्वारा दिए गए पथ का अनुसरण करती है, जहाँ $x$ इमारत से क्षैतिज दूरी है तथा $h(x)$ गेंद की ऊँचाई है। गेंद अधिकतम कितनी ऊँचाई तक पहुँचेगी?

(iii) शत्रु का एक अपाचे हेलीकॉप्टर $f(x)=x^{2}+7$ वक्र द्वारा दिए गए पथ पर उड़ रहा है। एक सैनिक, जो बिन्दु $(1,2)$ पर स्थित है, हेलीकॉप्टर को तब गोली मारना चाहता है जब वह उसके सबसे निकट हो। न्यूनतम दूरी क्या है?

उपरोक्त प्रत्येक समस्या में एक बात सामान्य है, अर्थात् हम दिए गए फलनों के अधिकतम या न्यूनतम मान ज्ञात करना चाहते हैं। ऐसी समस्याओं से निपटने के लिए हम पहले औपचारिक रूप से किसी फलन के अधिकतम या न्यूनतम मान, स्थानीय अधिकतम व न्यूनतम बिंदुओं की परिभाषा देते हैं और ऐसे बिंदुओं को निर्धारित करने के लिए जाँच करते हैं।

परिभाषा 3 मान लीजिए $f$ एक फलन है जो एक अंतराल I पर परिभाषित है। तब

(a) $f$ को I में अधिकतम मान होना कहा जाता है, यदि I में एक बिंदु $c$ ऐसा अस्तित्व में है कि $f(c)>f(x)$, सभी $x \in I$ के लिए।

संख्या $f(c)$ को I में $f$ का अधिकतम मान कहा जाता है और बिंदु $c$ को I में $f$ का अधिकतम मान बिंदु कहा जाता है।

(b) $f$ को I में न्यूनतम मान होना कहा जाता है, यदि I में एक बिंदु $c$ ऐसा अस्तित्व में है कि $f(c)<f(x)$, सभी $x \in I$ के लिए।

इस स्थिति में संख्या $f(c)$ को I में $f$ का न्यूनतम मान कहा जाता है और बिंदु $c$ को इस स्थिति में I में $f$ का न्यूनतम मान बिंदु कहा जाता है।

(c) $f$ को I में चरम मान होना कहा जाता है यदि I में एक बिंदु $c$ ऐसा अस्तित्व में है कि $f(c)$ या तो I में $f$ का अधिकतम मान है या न्यूनतम मान है।

इस स्थिति में संख्या $f(c)$ को I में $f$ का चरम मान कहा जाता है और बिंदु $c$ को चरम बिंदु कहा जाता है।

टिप्पणी आकृति 6.7(a), (b) और (c) में हमने यह दिखाया है कि कुछ विशिष्ट फलनों के आलेख हमें किसी बिंदु पर अधिकतम मान और न्यूनतम मान खोजने में सहायता करते हैं। वास्तव में, आलेखों के माध्यम से हम किसी फलन का अधिकतम/न्यूनतम मान उस बिंदु पर भी खोज सकते हैं जहाँ वह अवकलनीय भी नहीं है (उदाहरण 15)।

चित्र 6.7

उदाहरण 14 फलन $f$ द्वारा दिए गए अधिकतम और न्यूनतम मान, यदि कोई हों, ज्ञात कीजिए $ f(x)=x^{2}, x \in \mathbf{R} . $

हल दिए गए फलन के आलेख से (चित्र 6.8), हमें प्राप्त होता है कि $f(x)=0$ यदि $x=0$. साथ ही $ f(x) \geq 0 \text{, सभी } x \in \mathbf{R} \text{ के लिए। } $

इसलिए, $f$ का न्यूनतम मान 0 है और $f$ के न्यूनतम मान का बिंदु $x=0$ है। आगे, यह फलन के आलेख से देखा जा सकता है कि $f$ का कोई अधिकतम मान नहीं है और इसलिए $\mathbf{R}$ में $f$ के अधिकतम मान का कोई बिंदु नहीं है।

चित्र 6.8

टिप्पणी यदि हम $f$ के प्रांत को केवल $[-2,1]$ तक सीमित करें, तो $f$ का अधिकतम मान $(-2)^{2}=4$ होगा, जो $x=-2$ पर है।

उदाहरण 15 फलन $f$ द्वारा दिए गए अधिकतम और न्यूनतम मान, यदि कोई हों, ज्ञात कीजिए, जहाँ $f(x)=|x|, x \in \mathbf{R}$।

हल दिए गए फलन के आलेख से (चित्र 6.9), ध्यान दीजिए कि

$$ f(x) \geq 0 \text{, सभी } x \in \mathbf{R} \text{ के लिए और } f(x)=0 \text{ यदि } x=0 \text{। } $$

इसलिए, फलन $f$ का न्यूनतम मान 0 है और $f$ के न्यूनतम मान का बिंदु $x=0$ है। साथ ही, आलेख स्पष्ट रूप से दिखाता है कि $f$ का $\mathbf{R}$ में कोई अधिकतम मान नहीं है और इसलिए $\mathbf{R}$ में अधिकतम मान का कोई बिंदु नहीं है।

आकृति 6.9

नोट

(i) यदि हम (f) के प्रांत को केवल ([-2,1]) तक सीमित कर दें, तो (f) का अधिकतम मान (|-2|=2) होगा।

(ii) यह ध्यान दिया जा सकता है कि उदाहरण 27 में फलन (f), (x=0) पर अवकलनीय नहीं है।

उदाहरण 16 फलन
[ f(x)=x, x \in(0,1) ]
का अधिकतम और न्यूनतम मान, यदि कोई हो, तो ज्ञात कीजिए।

हल दिया गया फलन अंतराल ((0,1)) में एक वर्धमान (कड़ाई से) फलन है। फलन (f) के आलेख (आकृति 6.10) से ऐसा प्रतीत होता है कि इसे अपने न्यूनतम मान 0 के सर्वाधिक निकट दाईं ओर तथा अधिकतम मान 1 के सर्वाधिक निकट बाईं ओर प्राप्त होना चाहिए। क्या ऐसे बिंदु उपलब्ध हैं? बिलकुल नहीं। ऐसे बिंदुओं को स्थित करना संभव नहीं है। वास्तव में, यदि कोई बिंदु (x_0), 0 के सर्वाधिक निकट है, तो हम पाते हैं कि (\frac{x_0}{2}<x_0) सभी (x_0 \in(0,1)) के लिए। इसी प्रकार, यदि (x_1), 1 के सर्वाधिक निकट है, तो (\frac{x_1+1}{2}>x_1) सभी (x_1 \in(0,1)) के लिए।

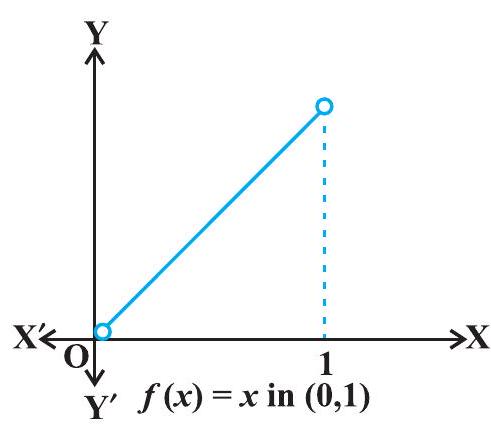
अतः दिया गया फलन अंतराल ((0,1)) में न तो अधिकतम मान रखता है और न ही न्यूनतम मान।

टिप्पणी पाठक देख सकता है कि उदाहरण 16 में, यदि हम फलन $f$ के प्रान्त में बिन्दुओं 0 और 1 को सम्मिलित करें, अर्थात् यदि हम फलन $f$ के प्रान्त को $[0,1]$ तक बढ़ा दें, तो फलन $f$ का न्यूनतम मान 0, $x=0$ पर तथा अधिकतम मान 1, $x=1$ पर है। वास्तव में, हमारे पास निम्नलिखित परिणाम हैं (इन परिणामों की प्रमाण वर्तमान पाठ की सीमा से बाहर है)

प्रत्येक एकात्मक फलन अपना अधिकतम/न्यूनतम मान फलन के परिभाषा प्रान्त के अन्तिम बिन्दुओं पर ग्रहण करता है।

एक और अधिक सामान्य परिणाम है प्रत्येक संतत फलन एक बन्द अन्तराल पर अधिकतम तथा न्यूनतम मान रखता है।

नोट एकात्मक फलन $f$ से हमारा तात्पर्य एक ऐसे फलन से है जो अन्तराल $I$ में या तो वर्धमान है या ह्रासमान है।

एक बन्द अन्तराल पर परिभाषित फलन के अधिकतम और न्यूनतम मानों पर इस खण्ड में आगे चर्चा की जाएगी।

आइए अब हम एक फलन के ग्राफ का अवलोकन करें जैसा कि चित्र 6.11 में दिखाया गया है। ध्यान दें कि ग्राफ पर बिंदुओं $A, B, C$ और $D$ पर फलन अपना स्वभाव घटते से बढ़ते या बढ़ते से घटते में बदलता है। इन बिंदुओं को दिए गए फलन के मोड़ बिंदु (turning points) कहा जा सकता है। इसके अतिरिक्त, ध्यान दें कि मोड़ बिंदुओं पर ग्राफ में या तो एक छोटी पहाड़ी या एक छोटी घाटी होती है। लगभग यह कहा जा सकता है कि फलन के पास प्रत्येक बिंदु $A$ और $C$ के किसी आस-पास के क्षेत्र (अंतराल) में न्यूनतम मान है जो अपनी-अपनी घाटियों के तल पर स्थित हैं। इसी प्रकार, फलन के पास बिंदुओं $B$ और $D$ के किसी आस-पास के क्षेत्र में अधिकतम मान है जो अपनी-अपनी पहाड़ियों के शिखर पर स्थित हैं। इस कारण से, बिंदुओं $A$ और $C$ को फलन के स्थानीय न्यूनतम मान (या सापेक्ष न्यूनतम मान) के बिंदु माना जा सकता है और बिंदुओं $B$ और $D$ को फलन के स्थानीय अधिकतम मान (या सापेक्ष अधिकतम मान) के बिंदु माना जा सकता है। फलन के स्थानीय अधिकतम मान और स्थानीय न्यूनतम मान को क्रमशः फलन के स्थानीय उच्चिष्क (local maxima) और स्थानीय निम्निष्क (local minima) कहा जाता है।

चित्र 6.11

अब ह औपचारिक रूप से निम्नलिखित परिभाषा देते हैं

परिभाषा 4 मान लीजिए $f$ एक वास्तविक मान वाला फलन है और मान लीजिए $c$ फलन $f$ के प्रांत का एक आंतरिक बिंदु है। तब

(a) $c$ को स्थानीय उच्चिष्क का बिंदु कहा जाता है यदि एक $h>0$ इस प्रकार है कि

$ f(c) \geq f(x) \text{, सभी } x \text{ के लिए }(c-h, c+h), x \neq c $

मान $f(c)$ को $f$ का स्थानीय अधिकतम मान कहा जाता है।

(b) $c$ को स्थानीय न्यूनतम बिंदु कहा जाता है यदि कोई $h>0$ ऐसा है कि

$ f(c) \leq f(x) \text{, सभी } x \text{ के लिए }(c-h, c+h) $

मान $f(c)$ को $f$ का स्थानीय न्यूनतम मान कहा जाता है।

ज्यामितीय रूप से, उपरोक्त परिभाषा कहती है कि यदि $x=c$, $f$ का स्थानीय अधिकतम बिंदु है, तो $c$ के आसपास $f$ का ग्राफ Fig 6.12(a) में दिखाए अनुसार होगा। ध्यान दें कि फलन $f$ अंतराल $(c-h, c)$ में बढ़ रहा है (अर्थात् $.f^{\prime}(x)>0)$ और अंतराल $(c, c+h)$ में घट रहा है (अर्थात् $.f^{\prime}(x)<0)$।

इससे संकेत मिलता है कि $f^{\prime}(c)$ शून्य होना चाहिए।

Fig 6.12

इसी प्रकार, यदि $c$, $f$ का स्थानीय न्यूनतम बिंदु है, तो $c$ के आसपास $f$ का ग्राफ Fig 6.14(b) में दिखाए अनुसार होगा। यहाँ $f$ अंतराल $(c-h, c)$ में घट रहा है (अर्थात् $.f^{\prime}(x)<0)$ और अंतराल $(c, c+h)$ में बढ़ रहा है (अर्थात् $.f^{\prime}(x)>0)$। यह फिर से संकेत देता है कि $f^{\prime}(c)$ शून्य होना चाहिए।

उपरोक्त चर्चा हमें निम्नलिखित प्रमेय (बिना प्रमाण) की ओर ले जाती है।

प्रमेय 2 मान लीजिए $f$ एक खुले अंतराल I पर परिभाषित फलन है। मान लीजिए $c \in I$ कोई बिंदु है। यदि $f$ का $x=c$ पर स्थानीय उच्चतम या स्थानीय निम्नतम है, तो या तो $f^{\prime}(c)=0$ है या $f$, $c$ पर अवकलनीय नहीं है।

टिप्पणी उपरोक्त प्रमेय का विलोम सत्य होना आवश्यक नहीं है, अर्थात् जिस बिंदु पर अवकलज शून्य होता है, वह बिंदु स्थानीय उच्चतम या स्थानीय निम्नतम का बिंदु होना आवश्यक नहीं है। उदाहरण के लिए, यदि $f(x)=x^{3}$ है, तो $f^{\prime}(x)=3 x^{2}$ और इसलिए $f^{\prime}(0)=0$ है। लेकिन 0 न तो स्थानीय उच्चतम का बिंदु है और न ही स्थानीय निम्नतम का बिंदु है (चित्र 6.13)।

नोट एक फलन $f$ के प्रांत का एक बिंदु $c$ जिस पर या तो $f^{\prime}(c)=0$ हो या $f$ अवकलनीय न हो, $f$ का एक क्रिटिकल बिंदु कहलाता है। ध्यान दें कि यदि $f$, $c$ पर संतत है और $f^{\prime}(c)=0$ है, तो एक $h>0$ का अस्तित्व होता है जिससे $f$, अंतराल $(c-h, c+h)$ में अवकलनीय होता है।

चित्र 6.13

अब हम स्थानीय उच्चतम या स्थानीय निम्नतम के बिंदुओं को खोजने के लिए केवल प्रथम कोटि के अवकलज का उपयोग करते हुए एक कार्यकारी नियम देंगे।

प्रमेय 3 (प्रथम अवकलज परीक्षण) मान लीजिए $f$ एक खुले अंतराल I पर परिभाषित फलन है। मान लीजिए $f$, I में एक क्रिटिकल बिंदु $c$ पर संतत है। तब

(i) यदि $f^{\prime}(x)$ का चिह्न $x$ के $c$ से बढ़ने पर धनात्मक से ऋणात्मक में बदलता है, अर्थात् यदि $f^{\prime}(x)>0$ हर बिन्दु पर पर्याप्त निकट और $c$ के बाईं ओर हो, और $f^{\prime}(x)<0$ हर बिन्दु पर पर्याप्त निकट और $c$ के दाईं ओर हो, तो $c$ स्थानीय उच्चतम का बिन्दु है।

(ii) यदि $f^{\prime}(x)$ का चिह्न $x$ के $c$ से बढ़ने पर ऋणात्मक से धनात्मक में बदलता है, अर्थात् यदि $f^{\prime}(x)<0$ हर बिन्दु पर पर्याप्त निकट और $c$ के बाईं ओर हो, और $f^{\prime}(x)>0$ हर बिन्दु पर पर्याप्त निकट और $c$ के दाईं ओर हो, तो $c$ स्थानीय न्यूनतम का बिन्दु है।

(iii) यदि $f^{\prime}(x)$ का चिह्न $x$ के $c$ से बढ़ने पर नहीं बदलता है, तो $c$ न तो स्थानीय उच्चतम का बिन्दु है और न ही स्थानीय न्यूनतम का बिन्दु है। वास्तव में, ऐसा बिन्दु झुकाव बिन्दु कहलाता है (चित्र 6.13)।

टिप्पणी यदि $c$ फलन $f$ का स्थानीय उच्चतम बिन्दु है, तो $f(c)$ फलन $f$ का स्थानीय अधिकतम मान है। इसी प्रकार, यदि $c$ फलन $f$ का स्थानीय न्यूनतम बिन्दु है, तो $f(c)$ फलन $f$ का स्थानीय न्यूनतम मान है।

चित्र 6.13 और 6.14, प्रमेय 3 को ज्यामितीय रूप से समझाते हैं।

चित्र 6.14

उदाहरण 17 फलन $f$ जिसके द्वारा दिया गया है $f(x)=x^{3}-3 x+3$, के सभी स्थानीय उच्चतम और स्थानीय न्यूनतम बिन्दु ज्ञात कीजिए।

हल हमारे पास

$$ \begin{array}{lrl} & f(x) & =x^3-3 x+3 \ \text{ या } & f^{\prime}(x) & =3 x^2-3=3(x-1)(x+1) \ \text{ या } & f^{\prime}(x) &=0 \text{ बिंदु } x=1 \text{ और } x=-1 \text{ पर} \end{array} $$

इस प्रकार, $x= \pm 1$ केवल महत्वपूर्ण बिंदु हैं जो संभवतः $f$ के स्थानीय उच्चतम और/या स्थानीय न्यूनतम बिंदु हो सकते हैं। आइए पहले बिंदु $x=1$ की जाँच करें।

ध्यान दें कि 1 के निकट और 1 के दाईं ओर के मानों के लिए, $f^{\prime}(x)>0$ और 1 के निकट और 1 के बाईं ओर के मानों के लिए, $f^{\prime}(x)<0$ है। इसलिए, प्रथम अवकलज परीक्षण द्वारा, $x=1$ एक स्थानीय न्यूनतम बिंदु है और स्थानीय न्यूनतम मान $f(1)=1$ है। $x=-1$ के मामले में, ध्यान दें कि -1 के निकट और -1 के बाईं ओर के मानों के लिए, $f^{\prime}(x)>0$ है और -1 के निकट और -1 के दाईं ओर के मानों के लिए, $f^{\prime}(x)<0$ है। इसलिए, प्रथम अवकलज परीक्षण द्वारा, $x=-1$ एक स्थानीय उच्चतम बिंदु है और स्थानीय उच्चतम मान $f(-1)=5$ है।

$ \begin{array}{|c|c|c|} \hline & \text{ x के मान } & \text{ } f^{\prime}(x)=3(x-1)(x+1) \text{ का चिह्न } \ \hline {\begin{array}{l} \text{ 1 के निकट } \end{array}} & \text{ दाईं ओर (मान लीजिए 1.1 आदि) } & > 0 \ \hline & \text{ बाईं ओर (मान लीजिए 0.9 आदि) } & <0 \ \hline \text{ -1 के निकट } & \text{ दाईं ओर (मान लीजिए -0.9 आदि) } & <0 \ \hline & \text{ बाईं ओर (मान लीजिए -1.1 आदि) } & >0 \ \hline \end{array} $

उदाहरण 18 फलन $f$ के सभी स्थानीय उच्चतम और स्थानीय न्यूनतम बिंदु ज्ञात कीजिए जो दिया गया है

हल हमारे पास

$$ \begin{array}{lrl} & f(x) & =2 x^{3}-6 x^{2}+6 x+5 \\ \text{ या }& f^{\prime}(x) & =6 x^{2}-12 x+6=6(x-1)^{2} \\ \text{ या }& f^{\prime}(x) & =0 \quad \text{ पर } \quad x=1 \end{array} $$

इस प्रकार, $x=1$ फलन $f$ का एकमात्र क्रिटिकल बिंदु है। अब हम इस बिंदु की जाँच करेंगे कि यह $f$ के स्थानीय उच्चतम और/या स्थानीय न्यूनतम के लिए है या नहीं। ध्यान दीजिए कि $f^{\prime}(x) \geq 0$, सभी $x \in \mathbf{R}$ के लिए और विशेष रूप से $f^{\prime}(x)>0$, 1 के निकट और 1 के बाएँ तथा दाएँ मानों के लिए है। इसलिए, प्रथम अवकलज परीक्षण द्वारा, बिंदु $x=1$ न तो स्थानीय उच्चतम का बिंदु है और न ही स्थानीय न्यूनतम का बिंदु है। अतः $x=1$ एक उल्ट बिंदु है।

टिप्पणी कोई यह नोट कर सकता है कि चूँकि उदाहरण 30 में $f^{\prime}(x)$ कभी भी $\mathbf{R}$ पर अपना चिह्न नहीं बदलता, $f$ के ग्राफ में कोई मोड़ बिंदु नहीं है और इसलिए कोई स्थानीय उच्चतम या स्थानीय न्यूनतम बिंदु नहीं है।

अब हम किसी दिए गए फलन के स्थानीय उच्चतम और स्थानीय न्यूनतम की जाँच करने के लिए एक अन्य परीक्षण देंगे। यह परीक्षण प्रथम अवकलज परीक्षण की तुलना में अक्सर लगाना आसान होता है।

प्रमेय 4 (द्वितीय अवकलज परीक्षण) मान लीजिए $f$ एक फलन है जो किसी अंतराल I पर परिभाषित है और $c \in I$। मान लीजिए $f$, $c$ पर द्विअवकलनीय है। तब

(i) $x=c$ स्थानीय उच्चतम का बिंदु है यदि $f^{\prime}(c)=0$ और $f^{\prime \prime}(c)<0$

मान $f(c)$ फलन $f$ का स्थानीय अधिकतम मान है।

(ii) $x=c$ स्थानीय न्यूनतम का बिंदु है यदि $f^{\prime}(c)=0$ और $f^{\prime \prime}(c)>0$

इस स्थिति में, $f(c)$ फलन $f$ का स्थानीय न्यूनतम मान है।

(iii) परीक्षण विफल हो जाता है यदि $f^{\prime}(c)=0$ और $f^{\prime \prime}(c)=0$।

इस स्थिति में, हम पहले अवकलज परीक्षण पर लौटते हैं और यह पता लगाते हैं कि $c$ स्थानीय उच्चतम, स्थानीय न्यूनतम या एक वक्रता बिंदु है या नहीं।

नोट चूँकि $f$, $c$ पर दो बार अवकलनीय है, हमारा तात्पर्य है कि $f$ का द्वितीय क्रम अवकलज $c$ पर विद्यमान है।

उदाहरण 19 फलन $f$ का स्थानीय न्यूनतम मान ज्ञात कीजिए जो $f(x)=3+|x|$, $x \in \mathbf{R}$ द्वारा दिया गया है।

हल ध्यान दीजिए कि दिया गया फलन $x=0$ पर अवकलनीय नहीं है। इसलिए, द्वितीय अवकलज परीक्षण विफल हो जाता है। आइए पहले अवकलज परीक्षण का प्रयास करें। ध्यान दीजिए कि 0, $f$ का एक महत्वपूर्ण बिंदु है। अब 0 के बाईं ओर, $f(x)=3-x$ और इसलिए $f^{\prime}(x)=-1<0$। साथ ही

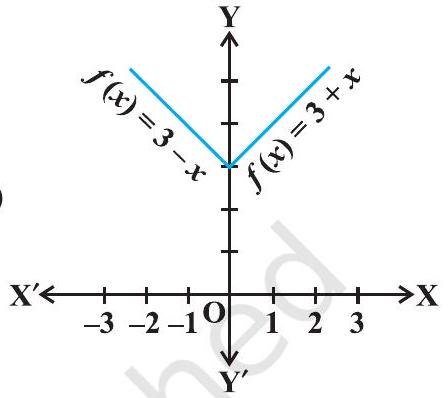
चित्र 6.15 0 के दाईं ओर, $f(x)=3+x$ और इसलिए $f^{\prime}(x)=1>0$। इसलिए, पहले अवकलज परीक्षण द्वारा, $x=$ 0, $f$ का एक स्थानीय न्यूनतम बिंदु है और $f$ का स्थानीय न्यूनतम मान $f(0)=3$ है।

उदाहरण 20 फलन $f$ का स्थानीय उच्चतम और स्थानीय न्यूनतम मान ज्ञात कीजिए जो

$ f(x)=3 x^{4}+4 x^{3}-12 x^{2}+12 $

द्वारा दिया गया है।

हल हमारे पास

$f(x)=3 x^{4}+4 x^{3}-12 x^{2}+12$

या & $f^{\prime}(x)=12 x^{3}+12 x^{2}-24 x=12 x(x-1)(x+2)$

या & $f^{\prime}(x)=0$ पर $x=0$, $x=1$ और $x=-2$।

अब & $f^{\prime \prime}(x)=36 x^{2}+24 x-24=12(3 x^{2}+2 x-2)$

$$ \left\{\begin{array}{c} f^{\prime \prime}(0)=-24<0 \\ f^{\prime \prime}(1)=36>0 \\ f^{\prime \prime}(-2)=72>0 \end{array}\right. $$

इसलिए, द्वितीय अवकलज परीक्षण द्वारा, $x=0$ स्थानीय उच्चतम बिंदु है और $x=0$ पर $f$ का स्थानीय उच्चतम मान $f(0)=12$ है जबकि $x=1$ और $x=-2$ स्थानीय निम्नतम बिंदु हैं और $x=-1$ और -2 पर $f$ के स्थानीय निम्नतम मान क्रमशः $f(1)=7$ और $f(-2)=-20$ हैं।

उदाहरण 21 फलन $f$ जो f(x)=2 x^{3}-6 x^{2}+6 x+5 द्वारा दिया गया है, के सभी स्थानीय उच्चतम और स्थानीय निम्नतम बिंदु ज्ञात कीजिए।

हल हमारे पास

$$ \text{या} \qquad \left\{\begin{array}{1}& f(x)=2 x^{3}-6 x^{2}+6 x+5 \\ \end{array}\right. $$

$$ \begin{aligned} & \left\{\begin{array}{l} f^{\prime}(x)=6 x^{2}-12 x+6=6(x-1)^{2} \\ f^{\prime \prime}(x)=12(x-1) \end{array}\right. \end{aligned} $$

अब $f^{\prime}(x)=0$ देता है $x=1$. साथ ही $f^{\prime \prime}(1)=0$. इसलिए, इस मामले में द्वितीय अवकलज परीक्षण विफल हो जाता है। इसलिए, हम पहले अवकलज परीक्षण पर वापस जाएंगे।

हम पहले ही देख चुके हैं (उदाहरण 18) कि, पहले अवकलज परीक्षण का उपयोग करके, $x=1$ न तो स्थानीय उच्चतम बिंदु है और न ही स्थानीय निम्नतम बिंदु है और इसलिए यह एक झुकाव बिंदु है।

उदाहरण 22 दो धनात्मक संख्याएं ज्ञात कीजिए जिनका योग 15 है और जिनके वर्गों का योग न्यूनतम है।

हल मान लीजिए संख्याओं में से एक $x$ है। तब दूसरी संख्या $(15-x)$ है। मान लीजिए $S(x)$ इन संख्याओं के वर्गों के योग को दर्शाता है। तब या

$$ S(x)=x^{2}+(15-x)^{2}=2 x^{2}-30 x+225 $$

$$ \begin{gathered} \left\{\begin{array}{l} S^{\prime}(x)=4 x-30 \\ S^{\prime \prime}(x)=4 \end{array}\right. \end{gathered} $$

अब $S^{\prime}(x)=0$ से $x=\frac{15}{2}$ मिलता है। साथ ही $S^{\prime \prime}(\frac{15}{2})=4>0$ है। इसलिए द्वितीय अवकलज परीक्षण से, $x=\frac{15}{2}$ स्थानीय न्यूनतम बिंदु है। अतः संख्याओं के वर्गों का योग न्यूनतम तब होता है जब संख्याएँ $\frac{15}{2}$ और $15-\frac{15}{2}=\frac{15}{2}$ हों।

टिप्पणी उदाहरण 34 की भाँति आगे बढ़कर कोई यह सिद्ध कर सकता है कि दो धनात्मक संख्याएँ, जिनका योग $k$ है और जिनके वर्गों का योग न्यूनतम है, वे $\frac{k}{2}$ और $\frac{k}{2}$ हैं।

उदाहरण 23 बिंदु $(0, c)$ की परवलय $y=x^{2}$ से न्यूनतम दूरी ज्ञात कीजिए, जहाँ $\frac{1}{2} \leq c \leq 5$ है।

हल मान लीजिए $(h, k)$ परवलय $y=x^{2}$ पर कोई बिंदु है। मान लीजिए $D$ बिंदु $(h, k)$ और $(0, c)$ के बीच अभीष्ट दूरी है। तब

$$ \begin{equation*} \mathrm{D}=\sqrt{(h-0)^{2}+(k-c)^{2}}=\sqrt{h^{2}+(k-c)^{2}} \tag{1} \end{equation*} $$

चूँकि $(h, k)$ परवलय $y=x^{2}$ पर स्थित है, हमें $k=h^{2}$ मिलता है। इसलिए (1) से

$$ \mathrm{D} \equiv \mathrm{D}(k)=\sqrt{k+(k-c)^{2}} $$

या $\mathrm{D}^{\prime}(k)=\frac{1+2(k-c)}{\sqrt{k+(k-c)^{2}}}$

अब $\mathrm{D}^{\prime}(k)=0 \text { से } k=\frac{2 c-1}{2}$

ध्यान दीजिए कि जब $k<\frac{2 c-1}{2}$, तब $2(k-c)+1<0$, अर्थात् $D^{\prime}(k)<0$। साथ ही जब $k>\frac{2 c-1}{2}$, तब $D^{\prime}(k)>0$। इसलिए प्रथम अवकलज परीक्षण से, $D(k)$ बिंदु $k=\frac{2 c-1}{2}$ पर न्यूनतम है।

अतः अभीष्ट न्यूनतम दूरी दी गई है

$$ \mathrm{D}\left(\frac{2 c-1}{2}\right)=\sqrt{\frac{2 c-1}{2}+\left(\frac{2 c-1}{2}-c\right)^{2}}=\frac{\sqrt{4 c-1}}{2} \text { } $$

ध्यान दें पाठक ध्यान दे सकता है कि उदाहरण 35 में, हमने द्वितीय अवकलज परीक्षण के बजाय प्रथम अवकलज परीक्षण का प्रयोग किया है क्योंकि पूर्ववाला आसान और छोटा है।

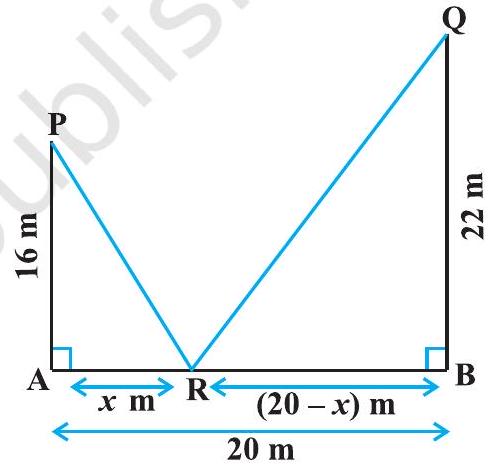
उदाहरण 24 मान लीजिए $AP$ और $BQ$ बिंदुओं $A$ और $B$ पर क्रमशः दो ऊर्ध्वाध्र खंभे हैं। यदि $AP=16 m, BQ=22 m$ और $A B=20 m$ है, तो बिंदु $A$ से $AB$ पर स्थित बिंदु $R$ की दूरी ज्ञात कीजिए ताकि $R P^{2}+R Q^{2}$ न्यूनतम हो।

हल मान लीजिए $R$, $AB$ पर एक बिंदु है ताकि $AR=x m$। तब $RB=(20-x) m$ (चूँकि $AB=20 m$)। चित्र 6.16 से, हम पाते हैं

$$ \begin{aligned} & \mathrm{RP}^{2}=\mathrm{AR}^{2}+\mathrm{AP}^{2} \\ \end{aligned} $$

और $R Q^{2}=R B^{2}+B Q^{2}$

चित्र 6.16

इसलिए $ \mathrm{RP}^{2}+\mathrm{RQ}^{2}=\mathrm{AR}^{2}+\mathrm{AP}^{2}+\mathrm{RB}^{2}+\mathrm{BQ}^{2}$ $$ \begin{aligned} & =x^{2}+(16)^{2}+(20-x)^{2}+(22)^{2} \\ & =2 x^{2}-40 x+1140 \end{aligned} $$

मान लीजिए $S \equiv S(x)=RP^{2}+RQ^{2}=2 x^{2}-40 x+1140$

इसलिए $S^{\prime}(x)=4 x-40$

अब $S^{\prime}(x)=0$ देता है $x=10$। साथ ही $S^{\prime \prime}(x)=4>0$, सभी $x$ के लिए और इसलिए $S^{\prime \prime}(10)>0$। इसलिए, द्वितीय अवकलज परीक्षण द्वारा, $x=10$, $S$ के स्थानीय न्यूनतम का बिंदु है। इस प्रकार, $AB$ पर $A$ से $R$ की दूरी $AR=x=10 m$ है।

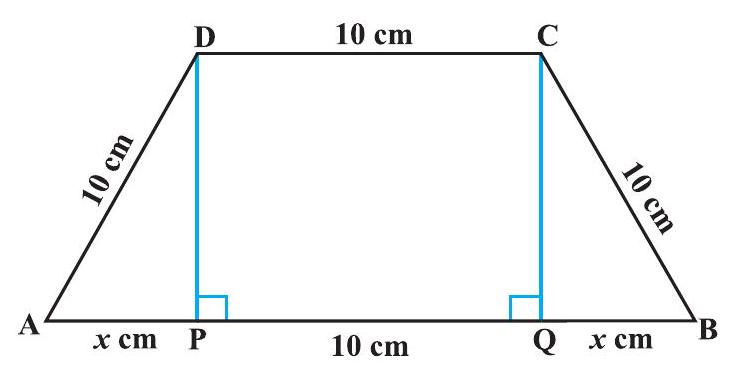
उदाहरण 25 यदि एक समलंब की तीन भुजाओं की लंबाई, आधार को छोड़कर, 10 सेमी के बराबर है, तो समलंब का क्षेत्रफल ज्ञात कीजिए जब वह अधिकतम हो।

हल आवश्यक समलंब चित्र 6.17 में दिया गया है। AB पर लंब DP और CQ खींचिए। मान लीजिए AP = x सेमी। ध्यान दीजिए कि △APD ~ △BQC है। इसलिए, QB = x सेमी। साथ ही, पाइथागोरस प्रमेय से, DP = QC = √(100 - x²)। मान लीजिए A समलंब का क्षेत्रफल है। तब

चित्र 6.17

$$ \begin{aligned} \mathrm{A} & \equiv \mathrm{A}(x) \ & = \frac{1}{2} \text{ (समानांतर भुजाओं का योग) (ऊंचाई)} \ & = \frac{1}{2}(2x + 10 + 10)\left(\sqrt{100 - x^{2}}\right) \ & = (x + 10)\left(\sqrt{100 - x^{2}}\right) \end{aligned} $$

या

$$ \begin{aligned} \mathrm{A}^{\prime}(x) & = (x + 10) \frac{(-2x)}{\sqrt{100 - x^{2}}} + \left(\sqrt{100 - x^{2}}\right) \ & = \frac{-2x^{2} - 10x + 100}{\sqrt{100 - x^{2}}} \end{aligned} $$

अब (\quad A^{\prime}(x) = 0) देता है (2x^{2} + 10x - 100 = 0), अर्थात्, (x = 5) और (x = -10).

चूंकि x दूरी को दर्शाता है, यह ऋणात्मक नहीं हो सकता। इसलिए, (x = 5). अब

$$ \begin{aligned} A^{\prime \prime}(x) & =\frac{\sqrt{100-x^{2}}(-4 x-10)-(-2 x^{2}-10 x+100) \frac{(-2 x)}{2 \sqrt{100-x^{2}}}}{100-x^{2}} \ & =\frac{2 x^{3}-300 x-1000}{(100-x^{2})^{\frac{3}{2}}} \text{ (सरलीकरण पर)} \ A^{\prime \prime}(5) & =\frac{2(5)^{3}-300(5)-1000}{(100-(5)^{2})^{\frac{3}{2}}}=\frac{-2250}{75 \sqrt{75}}=\frac{-30}{\sqrt{75}}<0 \end{aligned} $$

इस प्रकार, समलंब का क्षेत्रफल x=5 पर अधिकतम है और क्षेत्रफल निम्नलिखित है

$$ A(5)=(5+10) \sqrt{100-(5)^{2}}=15 \sqrt{75}=75 \sqrt{3} cm^{2} $$

उदाहरण 26 सिद्ध कीजिए कि दिए गए शंकु में अंतर्गत निहित अधिकतम वक्र पृष्ठीय क्षेत्रफल वाले लंब वृत्तीय बेलन की त्रिज्या शंकु की त्रिज्या की आधी होती है।

हल माना OC=r शंकु की त्रिज्या है और OA=h इसकी ऊंचाई है। माना एक बेलन जिसकी त्रिज्या OE=x दिए गए शंकु में अंतर्गत निहित है (चित्र 6.18)। बेलन की ऊंचाई QE निम्नलिखित है

$ \begin{array}{llll} \quad & \frac{QE}{OA} & =\frac{EC}{OC} \quad(\text{ चूंकि } \Delta QEC \sim \Delta AOC) \ \text{ या } & \frac{QE}{h} & =\frac{r-x}{r} \ \text{ या } & QE & =\frac{h(r-x)}{r} \end{array} $

माना S दिए गए बेलन का वक्र पृष्ठीय क्षेत्रफल है। तब

$$ \begin{aligned} & S \equiv S(x)=\frac{2 \pi x h(r-x)}{r}=\frac{2 \pi h}{r}\left(r x-x^{2}\right) \ & \left\{\begin{array}{l} S^{\prime}(x)=\frac{2 \pi h}{r}(r-2 x) \ S^{\prime \prime}(x)=\frac{-4 \pi h}{r} \end{array}\right. \end{aligned} $$

अब (S^{\prime}(x)=0) देता है (x=\frac{r}{2})। चूँकि (S^{\prime \prime}(x)<0) सभी (x) के लिए, (S^{\prime \prime}(\frac{r}{2})<0)। इसलिए (x=\frac{r}{2}) बिंदु (S) का उच्चतम बिंदु है। अतः, शंकु में अंकित अधिकतम वक्र पृष्ठीय क्षेत्रफल वाले बेलन की त्रिज्या उस शंकु की त्रिज्या की आधी होती है।

6.4.1 एक बंद अंतराल में फलन के अधिकतम और न्यूनतम मान

आइए एक फलन (f) पर विचार करें जो (f(x)=x+2, x \in(0,1)) द्वारा दिया गया है।

ध्यान दीजिए कि फलन ((0,1)) पर संतत है और न तो कोई अधिकतम मान रखता है और न ही कोई न्यूनतम मान। इसके अतिरिक्त, हम यह भी देख सकते हैं कि फलन के पास न तो कोई स्थानीय अधिकतम मान है और न ही कोई स्थानीय न्यूनतम मान।

हालाँकि, यदि हम (f) के प्रांत को बंद अंतराल ([0,1]) तक बढ़ा दें, तो (f) के पास अब भी स्थानीय अधिकतम (न्यूनतम) मान नहीं हो सकते हैं, लेकिन इसमें निश्चित रूप से अधिकतम मान (3=f(1)) और न्यूनतम मान (2=f(0)) होता है। (f) का अधिकतम मान 3 जो (x=1) पर है, को अंतराल ([0,1]) पर (f) का निरपेक्ष अधिकतम मान (वैश्विक अधिकतम या महत्तम मान) कहा जाता है। इसी प्रकार, (f) का न्यूनतम मान 2 जो (x=0) पर है, को अंतराल ([0,1]) पर (f) का निरपेक्ष न्यूनतम मान (वैश्विक न्यूनतम या न्यूनतम मान) कहा जाता है।

आकृति 6.19 में दिए गए एक संतत फलन के ग्राफ पर विचार करें जो बंद अंतराल ([a, d]) पर परिभाषित है। ध्यान दीजिए कि फलन (f) का (x=b) पर स्थानीय न्यूनतम है और स्थानीय

आकृति 6.19

न्यूनतम मान $f(b)$ है। फलन का स्थानीय उच्चतम भी $x=c$ पर है और स्थानीय उच्चतम मान $f(c)$ है।

इसके अतिरिक्त आकृति से यह स्पष्ट है कि $f$ का निरपेक्ष उच्चतम मान $f(a)$ है और निरपेक्ष न्यूनतम मान $f(d)$ है। आगे ध्यान दें कि $f$ का निरपेक्ष उच्चतम (न्यूनतम) मान, इसके स्थानीय उच्चतम (न्यूनतम) मान से भिन्न है।

हम अब दो परिणाम (बिना प्रमाण के) कथन करते हैं जो एक बंद अंतराल I पर फलन के निरपेक्ष उच्चतम और निरपेक्ष न्यूनतम मानों से संबंधित हैं।

प्रमेय 5 मान लीजिए $f$ अंतराल $I=[a, b]$ पर एक सतत फलन है। तब $f$ का निरपेक्ष उच्चतम मान होता है और $f$ इसे I में कम-से-कम एक बार प्राप्त करता है। इसी प्रकार, $f$ का निरपेक्ष न्यूनतम मान होता है और वह इसे I में कम-से-कम एक बार प्राप्त करता है।

प्रमेय 6 मान लीजिए $f$ एक बंद अंतराल I पर अवकलनीय फलन है और मान लीजिए $c$ इसका कोई आंतरिक बिंदु है। तब

(i) $f^{\prime}(c)=0$ यदि $f$ अपना निरपेक्ष उच्चतम मान $c$ पर प्राप्त करता है।

(ii) $f^{\prime}(c)=0$ यदि $f$ अपना निरपेक्ष न्यूनतम मान $c$ पर प्राप्त करता है।

उपरोक्त परिणामों के दृष्टिगत, हमारे पास एक दिए गए बंद अंतराल $[a, b]$ में फलन के निरपेक्ष उच्चतम और/या निरपेक्ष न्यूनतम मान ज्ञात करने के लिए निम्नलिखित कार्यविधि है।

कार्यविधि

चरण 1: अंतराल में फलन के सभी क्रांतिक बिंदु ज्ञात कीजिए, अर्थात् ऐसे बिंदु $x$ ज्ञात कीजिए जहाँ या तो $f^{\prime}(x)=0$ हो या $f$ अवकलनीय न हो।

चरण 2: अंतराल के अंत बिंदुओं को लीजिए।

चरण 3: इन सभी बिंदुओं पर (चरण 1 और 2 में सूचीबद्ध), $f$ के मानों की गणना कीजिए।

चरण 4: चरण 3 में गणना किए गए मानों में से $f$ के अधिकतम और न्यूनतम मानों की पहचान कीजिए। यह अधिकतम मान $f$ का निरपेक्ष अधिकतम (सबसे बड़ा) मान होगा और न्यूनतम मान $f$ का निरपेक्ष न्यूनतम (सबसे छोटा) मान होगा।

उदाहरण 27 एक फलन $f$ द्वारा दिए गए निरपेक्ष अधिकतम और न्यूनतम मानों को ज्ञात कीजिए जो अंतराल $[1,5]$ पर $f(x)=2 x^{3}-15 x^{2}+36 x+1$ द्वारा दिया गया है।

हल हमारे पास

$$ \begin{aligned} f(x) & =2 x^{3}-15 x^{2}+36 x+1 \end{aligned} $$ $ \begin{aligned} या \qquad f^{\prime}(x) & =6 x^{2}-30 x+36=6(x-3)(x-2) \end{aligned} $

ध्यान दीजिए कि $f^{\prime}(x)=0$ से $x=2$ और $x=3$ प्राप्त होते हैं।

अब हम इन बिंदुओं पर और अंतराल $[1,5]$ के अंत बिंदुओं पर, अर्थात् $x=1, x=2, x=3$ और $x=5$ पर $f$ के मानों का मूल्यांकन करेंगे। इसलिए

$$ \begin{aligned} & f(1)=2\left(1^{3}\right)-15\left(1^{2}\right)+36(1)+1=24 \\ & f(2)=2\left(2^{3}\right)-15\left(2^{2}\right)+36(2)+1=29 \\ & f(3)=2\left(3^{3}\right)-15\left(3^{2}\right)+36(3)+1=28 \\ & f(5)=2\left(5^{3}\right)-15\left(5^{2}\right)+36(5)+1=56 \end{aligned} $$

इस प्रकार, हम निष्कर्ष निकालते हैं कि $f$ का $[1,5]$ पर निरपेक्ष अधिकतम मान 56 है, जो $x=5$ पर होता है, और $f$ का $[1,5]$ पर निरपेक्ष न्यूनतम मान 24 है जो $x=1$ पर होता है।

उदाहरण 28 एक फलन (f) का निरपेक्ष उच्चतम और निम्नतम मान ज्ञात कीजिए जो (f(x)=12 x^{\frac{4}{3}}-6 x^{\frac{1}{3}}, x \in[-1,1]) द्वारा दिया गया है।

हल हमारे पास

$$ \begin{aligned} & f(x)=12 x^{\frac{4}{3}}-6 x^{\frac{1}{3}} \end{aligned} $$ $ \begin{aligned} या \qquad & f^{\prime}(x)=16 x^{\frac{1}{3}}-\frac{2}{x^{\frac{2}{3}}}=\frac{2(8 x-1)}{x^{\frac{2}{3}}} \end{aligned} $

इस प्रकार, (f^{\prime}(x)=0) देता है (x=\frac{1}{8})। आगे ध्यान दें कि (f^{\prime}(x)), (x=0) पर परिभाषित नहीं है। इसलिए क्रिटिकल बिंदु (x=0) और (x=\frac{1}{8}) हैं। अब क्रिटिकल बिंदुओं (x=0, \frac{1}{8}) और अंतराल के अंतिम बिंदुओं (x=-1) और (x=1) पर (f) का मान मूल्यांकन करने पर, हमारे पास

$$ \begin{aligned} f(-1) & =12\left(-1^{\frac{4}{3}}\right)-6\left(-1^{\frac{1}{3}}\right)=18 \\ f(0) & =12(0)-6(0)=0 \\ f\left(\frac{1}{8}\right) & =12\left(\frac{1}{8}\right)^{\frac{4}{3}}-6\left(\frac{1}{8}\right)^{\frac{1}{3}}=\frac{-9}{4} \\ f(1) & =12\left(1^{\frac{4}{3}}\right)-6\left(1^{\frac{1}{3}}\right)=6 \end{aligned} $$

अतः, हम निष्कर्ष निकालते हैं कि (f) का निरपेक्ष उच्चतम मान 18 है जो (x=-1) पर आता है और (f) का निरपेक्ष निम्नतम मान (\frac{-9}{4}) है जो (x=\frac{1}{8}) पर आता है।

उदाहरण 29 दुश्मन का एक अपाचे हेलीकॉप्टर वक्र (y=x^{2}+7) के अनुरूप उड़ रहा है। एक सैनिक, जो ((3,7)) पर स्थित है, हेलीकॉप्टर को तब मार गिराना चाहता है जब वह उसके सबसे निकट हो। निकटतम दूरी ज्ञात कीजिए।

हल प्रत्येक $x$ के मान के लिए, हेलीकॉप्टर की स्थिति बिंदु $(x, x^{2}+7)$ पर है। इसलिए, $(3,7)$ पर स्थित सैनिक और हेलीकॉप्टर के बीच की दूरी

$ \sqrt{(x-3)^{2}+(x^{2}+7-7)^{2}} \text{, अर्थात् } \sqrt{(x-3)^{2}+x^{4}} \text{ है। } $

$ मान लीजिए \qquad f(x)=(x-3)^{2}+x^{4} $

$ या \qquad f^{\prime}(x)=2(x-3)+4 x^{3}=2(x-1)\left(2 x^{2}+2 x+3\right) $

इस प्रकार, $f^{\prime}(x)=0$ से $x=1$ या $2 x^{2}+2 x+3=0$ प्राप्त होता है, जिसके कोई वास्तविक मूल नहीं हैं। साथ ही, कोई अंतराल के अंतिम बिंदु नहीं हैं जिन्हें उस समुच्चय में जोड़ा जाए जिसके लिए $f^{\prime}$ शून्य है, अर्थात् केवल एक बिंदु है, वह है $x=1$। इस बिंदु पर $f$ का मान $f(1)=(1-3)^{2}+(1)^{4}=5$ द्वारा दिया गया है। इस प्रकार, सैनिक और हेलीकॉप्टर के बीच की दूरी $\sqrt{f(1)}=\sqrt{5}$ है।

ध्यान दें कि $\sqrt{5}$ या तो एक अधिकतम मान या न्यूनतम मान है। चूँकि

$$ \sqrt{f(0)}=\sqrt{(0-3)^{2}+(0)^{4}}=3>\sqrt{5} \text { है, } $$

इसलिए यह सिद्ध होता है कि $\sqrt{5}$, $\sqrt{f(x)}$ का न्यूनतम मान है। अतः, सैनिक और हेलीकॉप्टर के बीच की न्यूनतम दूरी $\sqrt{5}$ है।

विविध उदाहरण

उदाहरण 30 एक कार $t=0$ सेकंड पर बिंदु $P$ से प्रारंभ होती है और बिंदु $Q$ पर रुकती है। द्वारा तय की गई दूरी $x$, मीटर में, $t$ सेकंड में

$$ x=t^{2}\left(2-\frac{t}{3}\right) \text { द्वारा दी गई है। } $$

इसके द्वारा $Q$ तक पहुँचने में लिया गया समय ज्ञात कीजिए और साथ ही $P$ और $Q$ के बीच की दूरी भी ज्ञात कीजिए।

हल मान लीजिए $v$ कार का $t$ सेकंड पर वेग है।

अब $ \begin{aligned} & x=t^{2}\left(2-\frac{t}{3}\right) \end{aligned} $

इसलिए $ \begin{aligned} & v=\frac{d x}{d t}=4 t-t^{2}=t(4-t) \end{aligned} $

इस प्रकार, $v=0$ से $t=0$ और/या $t=4$ मिलता है। अब $v=0$ बिन्दु $P$ पर तथा बिन्दु $Q$ पर भी है और $P$ पर, $t=0$ है। अतः $Q$ पर, $t=4$ है। इस प्रकार, कार बिन्दु $Q$ पर 4 सेकण्ड बाद पहुँचेगी। साथ ही 4 सेकण्ड में तय दूरी निम्न द्वारा दी गई है

$$ x] _{t=4}=4^{2}(2-\frac{4}{3})=16(\frac{2}{3})=\frac{32}{3} m $$

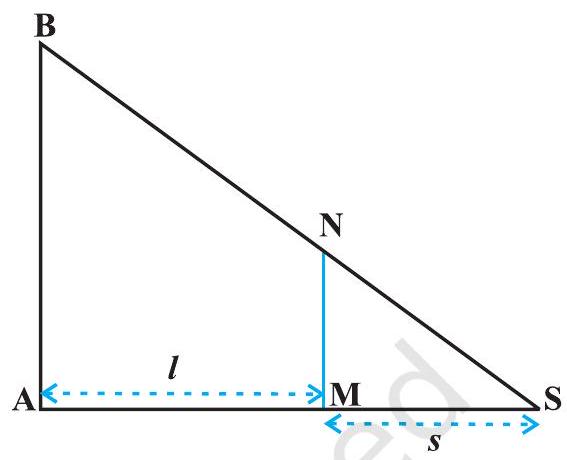
उदाहरण 32 एक 2 मीटर ऊँचा आदमी एक खंभे से जो 6 मीटर ऊँचा है, $5 km / h$ की एकसमान चाल से दूर चल रहा है। उसकी छाया की लम्बाई जिस दर से बढ़ रही है, वह ज्ञात कीजिए।

हल आकृति 6.21 में, मान लीजिए AB खंभा है, बत्ती स्थिति $B$ पर है और मान लीजिए $MN$ आदमी है किसी समय $t$ पर और मान लीजिए $AM=l$ मीटर है। तब, MS आदमी की छाया है। मान लीजिए MS $=s$ मीटर है।

ध्यान दीजिए कि $\triangle \mathrm{ASB} \sim \triangle \mathrm{MSN}$

या $\frac{\mathrm{MS}}{\mathrm{AS}}=\frac{\mathrm{MN}}{\mathrm{AB}}$

या $\mathrm{AS}=3 s$

आकृति 6.21

$\mathrm{MN}=2 \mathrm{~m}$ और $\mathrm{AB}=6 \mathrm{~m}$ (दिया गया है)

$\mathrm{AM}=3 s-s=2 s$ है। परन्तु $\mathrm{AM}=l$

इसलिए $\quad l=2 s$

चूँकि $\frac{d l}{d t}=5 km / h$.

अतः, छाया की लम्बाई $\frac{5}{2} km / h$ की दर से बढ़ती है।

उदाहरण 33 अन्तराल ज्ञात कीजिए जिनमें दिया गया फलन

$$ f(x)=\frac{3}{10} x^{4}-\frac{4}{5} x^{3}-3 x^{2}+\frac{36}{5} x+11 $$

(a) बढ़ रहा है (b) घट रहा है।

हल हमारे पास है

$$ f(x)=\frac{3}{10} x^{4}-\frac{4}{5} x^{3}-3 x^{2}+\frac{36}{5} x+11 $$ $$ \begin{aligned} f^{\prime}(x) & =\frac{3}{10}(4 x^{3})-\frac{4}{5}(3 x^{2})-3(2 x)+\frac{36}{5} \ & =\frac{6}{5}(x-1)(x+2)(x-3) \quad \text{ (सरलीकरण पर) } \end{aligned} $$

अब $f^{\prime}(x)=0$ देता है $x=1, x=-2$, या $x=3$। बिंदु $x=1,-2$, और 3 वास्तविक रेखा को चार असंयुक्त अंतरालों में विभाजित करते हैं, अर्थात्, $(-\infty,-2),(-2,1),(1,3)$ और $(3, \infty)$ (चित्र 6.22)।

चित्र 6.22

अंतराल $(-\infty,-2)$ पर विचार करें, अर्थात् जब $-\infty<x<-2$।

इस स्थिति में, हमारे पास $x-1<0, x+2<0$ और $x-3<0$ है।

(विशेष रूप से, ध्यान दें कि $x=-3$ के लिए, $f^{\prime}(x)=(x-1)(x+2)(x-3)=(-4)(-1)$ $(-6)<0)$

इसलिए, $\quad f^{\prime}(x)<0$ जब $-\infty<x<-2$।

इस प्रकार, फलन $f$ अंतराल $(-\infty,-2)$ में घट रहा है।

अंतराल $(-2,1)$ पर विचार करें, अर्थात् जब $-2<x<1$।

इस स्थिति में, हमारे पास $x-1<0, x+2>0$ और $x-3<0$ है

(विशेष रूप से, ध्यान दें कि $x=0$ के लिए, $f^{\prime}(x)=(x-1)(x+2)(x-3)=(-1)(2)(-3)$ $=6>0)$

इसलिए $ f^{\prime}(x)>0 \text{ जब }-2<x<1 \text{। } $

इस प्रकार, $ f \text{ अंतराल }(-2,1) \text{ में बढ़ रहा है। } $

अब अंतराल $(1,3)$ पर विचार करें, अर्थात् जब $1<x<3$। इस स्थिति में, हमारे पास $x-1>0, x+2>0$ और $x-3<0$ है।

$ तो, \qquad f^{\prime}(x)<0 \text{ जब } 1<x<3 \text{। } $

इस प्रकार, $f$ घट रहा है $(1,3)$ में।

अंत में, अंतराल $(3, \infty)$ पर विचार करें, अर्थात् जब $x>3$। इस स्थिति में, हमारे पास $x-1>0$, $x+2>0$ और $x-3>0$ है। इसलिए $f^{\prime}(x)>0$ जब $x>3$।

इस प्रकार, $f$ अंतराल $(3, \infty)$ में बढ़ रहा है।

उदाहरण 34 दिखाइए कि फलन $f$ जो दिया गया है

$ f(x)=\tan ^{-1}(\sin x+\cos x), x>0 $

हमेशा एक बढ़ता हुआ फलन है $0, \frac{\pi}{4}$ में।

हल हमारे पास

इसलिए $ \begin{aligned} f(x) & =\tan ^{-1}(\sin x+\cos x), x>0 \\ f^{\prime}(x) & =\frac{1}{1+(\sin x+\cos x)^{2}}(\cos x-\sin x) \\ & =\frac{\cos x-\sin x}{2+\sin 2 x} \end{aligned} $

ध्यान दें कि $2+\sin 2 x>0$ सभी $x$ के लिए $0, \frac{\pi}{4}$ में।

इसलिए $\qquad f^{\prime}(x)>0 \text{ यदि } \cos x-\sin x>0$

या $\qquad f^{\prime}(x)>0 \text{ यदि } \cos x>\sin x \text{ या } \cot x>1$

अब $\qquad \cot x>1 \text{ यदि } \tan x<1 \text{, अर्थात् यदि } 0<x<\frac{\pi}{4}$

इस प्रकार $\qquad f^{\prime}(x)>0 \text{ in } 0, \frac{\pi}{4}$

अतः $f$ बढ़ता हुआ फलन है $(0, \frac{\pi}{4})$ में।

उदाहरण 35 एक वृत्ताकार डिस्क जिसकी त्रिज्या $3 cm$ है, को गर्म किया जा रहा है। प्रसार के कारण, इसकी त्रिज्या $0.05 cm / s$ की दर से बढ़ रही है। ज्ञात कीजिए कि इसका क्षेत्रफल किस दर से बढ़ रहा है जब त्रिज्या $3.2 cm$ है।

हल मान लीजिए $r$ दी गई डिस्क की त्रिज्या है और $A$ इसका क्षेत्रफल है। तब

तब $\qquad \mathrm{A}=\pi r^{2}$

या $\qquad \frac{d A}{d t}=2 \pi r \frac{d r}{d t}$

अब त्रिज्या की अनुमानित वृद्धि दर $=d r=\frac{d r}{d t} \Delta t=0.05 cm / s$।

इसलिए, क्षेत्रफल में अनुमानित वृद्धि दर निम्नलिखित द्वारा दी जाती है

$ \begin{aligned} d A & =\frac{d A}{d t}(\Delta t)=2 \pi r(\frac{d r}{d t} \Delta t) \ & =2 \pi(3.2)(0.05)=0.320 \pi cm^{2} / s \quad(r=3.2 cm) \end{aligned} $

उदाहरण 36 एक खुले ऊपर वाले डिब्बे का निर्माण 3 मीटर × 8 मीटर के एल्युमिनियम की चादर के हर कोने से समान वर्ग काटकर और किनारों को मोड़कर किया जाना है। ऐसे सबसे बड़े डिब्बे का आयतन ज्ञात कीजिए।

हल मान लीजिए $x$ मीटर काटे गए वर्गों की भुजा की लंबाई है। तब डिब्बे की ऊँचाई $x$, लंबाई $8-2 x$ और चौड़ाई $3-2 x$ होगी (चित्र 6.23)। यदि $V(x)$ डिब्बे का आयतन है, तो

चित्र 6.23

$ \begin{aligned} V(x) & =x(3-2 x)(8-2 x) \ & =4 x^{3}-22 x^{2}+24 x \end{aligned} $

इसलिए $\qquad \begin{cases} V^{\prime}(x)=12 x^{2}-44 x+24=4(x-3)(3 x-2) \ V^{\prime \prime}(x)=24 x-44 \end{cases}$

अब $\qquad V^{\prime}(x)=0 \text{ देता है } x=3, \frac{2}{3} \text{। पर } x \neq 3 \text{ (क्यों?) }$

इस प्रकार, हमारे पास $x=\frac{2}{3}$ है। अब $V^{\prime \prime}(\frac{2}{3})=24(\frac{2}{3})-44=-28<0$।

इसलिए, $x=\frac{2}{3}$ अधिकतम बिंदु है, अर्थात यदि हम शीट के प्रत्येक कोने से $\frac{2}{3}$ मीटर भुजा का एक वर्ग काटकर निकालें और शेष शीट से एक डिब्बा बनाएं, तो इस प्रकार प्राप्त डिब्बे का आयतन सबसे बड़ा होगा और यह

$\mathrm{V}\left(\frac{2}{3}\right)=4\left(\frac{2}{3}\right)^{3}-22\left(\frac{2}{3}\right)^{2}+24\left(\frac{2}{3}\right)=\frac{200}{27} \mathrm{~m}^{3}$

उदाहरण 37 एक निर्माता $x$ वस्तुओं को ₹ $5-\frac{x}{100}$ प्रति वस्तु की दर से बेच सकता है। $x$ वस्तुओं का क्रय मूल्य ₹ $\frac{x}{5}+500$ है। वह अधिकतम लाभ कमाने के लिए कितनी वस्तुएँ बेचे?

हल मान लीजिए $S(x)$, $x$ वस्तुओं का विक्रय मूल्य है और मान लीजिए $C(x)$, $x$ वस्तुओं का क्रय मूल्य है। तब, हमारे पास

$$ S(x)=\left(5-\frac{x}{100}\right) x=5 x-\frac{x^{2}}{100} $$

और $\qquad \mathrm{C}(x)=\frac{x}{5}+500$

इस प्रकार, लाभ फलन $P(x)$ इस प्रकार दिया गया है

अर्थात $\qquad \mathrm{P}(x)=\mathrm{S}(x)-\mathrm{C}(x)=5 x-\frac{x^{2}}{100}-\frac{x}{5}-500$

$$ \mathrm{P}(x)=\frac{24}{5} x-\frac{x^{2}}{100}-500 $$

अब $\qquad P^{\prime}(x)=0$ देता है $x=240$. साथ ही $P^{\prime \prime}(x)=\frac{-1}{50}$. इसलिए $\qquad P^{\prime \prime}(240)=\frac{-1}{50}<0$

इस प्रकार, $x=240$ अधिकतम बिंदु है। अतः निर्माता अधिकतम लाभ तभी कमा सकता है, जब वह 240 वस्तुएँ बेचे।

सारांश

यदि कोई मात्रा y किसी अन्य मात्रा x के साथ किसी नियम y = f(x) को संतुष्ट करते हुए बदलती है, तो $\frac{dy}{dx}$ या (f’(x)) y में x के सापेक्ष परिवर्तन की दर को दर्शाता है और $\frac{dy}{dx}_{x=x_0}$ या (f’(x_0)) $\text{y में x के सापेक्ष परिवर्तन की दर को}$ $x = x_0$ पर दर्शाता है।
यदि दो चर x और y किसी अन्य चर t के सापेक्ष बदल रहे हैं, अर्थात यदि x = f(t) और y = g(t), तो श्रृंखला नियम द्वारा

$$ \frac{dy}{dx} = \frac{dy}{dt} \Big/ \frac{dx}{dt}, \text{ यदि } \frac{dx}{dt} \neq 0 $$

एक फलन f को इस प्रकार कहा जाता है:

(a) एक अंतराल (a, b) पर बढ़ता हुआ, यदि x₁ < x₂ हो (a, b) में ⇒ f(x₁) < f(x₂) सभी x₁, x₂ ∈ (a, b) के लिए।
वैकल्पिक रूप से, यदि f’(x) ≥ 0 हो प्रत्येक x ∈ (a, b) के लिए।

(b) (a, b) पर घटता हुआ, यदि
x₁ < x₂ हो (a, b) में ⇒ f(x₁) > f(x₂) सभी x₁, x₂ ∈ (a, b) के लिए।

(c) (a, b) में स्थिर, यदि f(x) = c हो सभी x ∈ (a, b) के लिए, जहाँ c एक नियतांक है।

• एक बिंदु c जो किसी फलन f के प्रांत में हो, जिस पर या तो f’(c) = 0 हो या f अवकलनीय न हो, f का एक आलोच्य बिंदु कहलाता है।
• प्रथम अवकलज परीक्षण: मान लीजिए f एक खुले अंतराल I पर परिभाषित फलन है। मान लीजिए f, I में एक आलोच्य बिंदु c पर संतत है। तब

(i) यदि $f^{\prime}(x)$ चिह्न धन से ऋण में बदलता है जैसे ही $x$, $c$ के माध्यम से बढ़ता है, अर्थात् यदि $f^{\prime}(x)>0$ होता है हर बिंदु पर जो पर्याप्त रूप से $c$ के निकट और उसके बाईं ओर है, और $f^{\prime}(x)<0$ होता है हर बिंदु पर जो पर्याप्त रूप से $c$ के निकट और उसके दाईं ओर है, तो $c$ स्थानीय उच्चतम का बिंदु है।

(ii) यदि $f^{\prime}(x)$ चिह्न ऋण से धन में बदलता है जैसे ही $x$, $c$ के माध्यम से बढ़ता है, अर्थात् यदि $f^{\prime}(x)<0$ होता है हर बिंदु पर जो पर्याप्त रूप से $c$ के निकट और उसके बाईं ओर है, और $f^{\prime}(x)>0$ होता है हर बिंदु पर जो पर्याप्त रूप से $c$ के निकट और उसके दाईं ओर है, तो $c$ स्थानीय न्यूनतम का बिंदु है।

(iii) यदि $f^{\prime}(x)$ चिह्न नहीं बदलता जैसे ही $x$, $c$ के माध्यम से बढ़ता है, तो $c$ न तो स्थानीय उच्चतम का बिंदु है और न ही स्थानीय न्यूनतम का बिंदु है। वास्तव में, ऐसा बिंदु वक्रता बिंदु कहलाता है।

• द्वितीय अवकलज परीक्षण मान लीजिए $f$ एक फलन है जो अंतराल I पर परिभाषित है और $c \in I$ है। मान लीजिए $f$, $c$ पर दो बार अवकलनीय है। तब

(i) $x=c$ स्थानीय उच्चतम का बिंदु है यदि $f^{\prime}(c)=0$ और $f^{\prime \prime}(c)<0$
मान $f(c)$ फलन $f$ का स्थानीय अधिकतम मान है।

(ii) $x=c$ स्थानीय न्यूनतम का बिंदु है यदि $f^{\prime}(c)=0$ और $f^{\prime \prime}(c)>0$
इस स्थिति में, $f(c)$ फलन $f$ का स्थानीय न्यूनतम मान है।

(iii) परीक्षण विफल हो जाता है यदि $f^{\prime}(c)=0$ और $f^{\prime \prime}(c)=0$ है।

इस स्थिति में, हम पहले अवकलज परीक्षण पर वापस जाते हैं और पता लगाते हैं कि $c$ उच्चतम का बिंदु है, न्यूनतम का बिंदु है या वक्रता बिंदु है।

• निरपेक उच्चतम और/या निरपेक न्यूनतम ज्ञात करने की कार्यविधि

चरण 1: अंतराल में फलन $f$ के सभी क्रिटिकल बिंदु खोजें, अर्थात् वे बिंदु $x$ जहाँ या तो $f^{\prime}(x)=0$ है या फिर $f$ अवकलनीय नहीं है।

चरण 2: अंतराल के अंतिम बिंदु लें।

चरण 3: इन सभी बिंदुओं (चरण 1 और 2 में सूचीबद्ध) पर फलन $f$ के मानों की गणना करें।

चरण 4: चरण 3 में परिकलित मानों में से फलन $f$ के अधिकतम और न्यूनतम मानों की पहचान करें। यह अधिकतम मान फलन $f$ का निरपेक्ष अधिकतम मान होगा और न्यूनतम मान फलन $f$ का निरपेक्ष न्यूनतम मान होगा।